内蒙古自治区包头市昆区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 如图,将棱长为6的正方体截去一个棱长为3的正方体后,得到一个新的几何体,这个几何体的主视图是( )
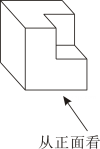 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,在 中, ,若 ,则 的长为( )
2. 如图,在 中, ,若 ,则 的长为( )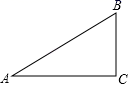 A、8 B、12 C、 D、3. 用配方法解一元二次方程 ,配方正确的是( ).A、 B、 C、 D、4. 若 与 都是反比例函数 图象上的点,则a的值是( )A、4 B、 C、2 D、5. 从下列命题中,随机抽取一个是真命题的概率是( )
A、8 B、12 C、 D、3. 用配方法解一元二次方程 ,配方正确的是( ).A、 B、 C、 D、4. 若 与 都是反比例函数 图象上的点,则a的值是( )A、4 B、 C、2 D、5. 从下列命题中,随机抽取一个是真命题的概率是( )⑴无理数都是无限小数;
⑵因式分解 ;
⑶棱长是 的正方体的表面展开图的周长一定是 ;
⑷两条对角线长分别为6和8的菱形的周长是40.
A、 B、 C、 D、16. 某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛36场,则参加此次比赛的球队数是( )A、6 B、7 C、8 D、97. 如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为( ) A、 B、 C、 D、8. 如图,在矩形 中, , ,点E在 边上, ,垂足为F.若 ,则线段 的长为( )
A、 B、 C、 D、8. 如图,在矩形 中, , ,点E在 边上, ,垂足为F.若 ,则线段 的长为( ) A、2 B、3 C、4 D、59. 现有两个不透明的袋子,一个装有2个红球、1个白球,另一个装有1个黄球、2个红球,这些球除颜色外完全相同,从两个袋子中各随机摸出1个球,摸出的两个球颜色相同的概率是( )A、 B、 C、 D、10. 已知两个直角三角形的三边长分别为3,4, 和6,8, ,且这两个直角三角形不相似,则 的值为( )A、 或 B、15 C、 D、11. 如图所示,过y轴正半轴上的任意一点P , 作x轴的平行线,分别与反比例函数 和 的图象交于点A和点B , 若点C是x轴上任意一点,连接 ,则 的面积为( )
A、2 B、3 C、4 D、59. 现有两个不透明的袋子,一个装有2个红球、1个白球,另一个装有1个黄球、2个红球,这些球除颜色外完全相同,从两个袋子中各随机摸出1个球,摸出的两个球颜色相同的概率是( )A、 B、 C、 D、10. 已知两个直角三角形的三边长分别为3,4, 和6,8, ,且这两个直角三角形不相似,则 的值为( )A、 或 B、15 C、 D、11. 如图所示,过y轴正半轴上的任意一点P , 作x轴的平行线,分别与反比例函数 和 的图象交于点A和点B , 若点C是x轴上任意一点,连接 ,则 的面积为( )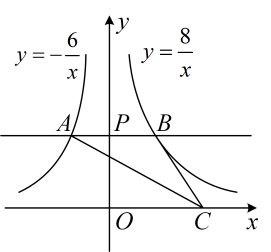 A、6 B、7 C、8 D、1412. 如图, , ,点A在 上,四边形 是矩形,连接 、 交于点E,连接 交 于点F.下列4个判断:① 平分 ;② ;③ ;④若点G是线段 的中点,则 为等腰直角三角形.正确判断的个数是( )
A、6 B、7 C、8 D、1412. 如图, , ,点A在 上,四边形 是矩形,连接 、 交于点E,连接 交 于点F.下列4个判断:① 平分 ;② ;③ ;④若点G是线段 的中点,则 为等腰直角三角形.正确判断的个数是( )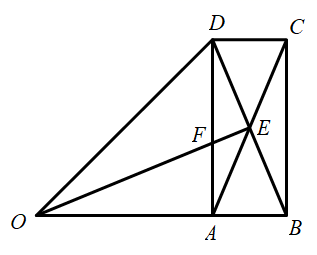 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
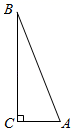
13. 如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cosA的值是 .
 14. 某校九(1)班准备举行一次演讲比赛,甲、乙、丙三人通过抽签方式决定出场顺序,则出场顺序恰好是甲、乙、丙的概率是.15. 一次函数 的图象与反比例函数 的图象的两个交点分别是 , ,则 .16. 一个三角形的两边长分别为2和5,第三边长是方程 的根,则该三角形的周长为.17. 如图所示,在四边形 中, , , .连接 , ,若 ,则 长度是 .
14. 某校九(1)班准备举行一次演讲比赛,甲、乙、丙三人通过抽签方式决定出场顺序,则出场顺序恰好是甲、乙、丙的概率是.15. 一次函数 的图象与反比例函数 的图象的两个交点分别是 , ,则 .16. 一个三角形的两边长分别为2和5,第三边长是方程 的根,则该三角形的周长为.17. 如图所示,在四边形 中, , , .连接 , ,若 ,则 长度是 .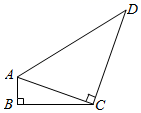 18. 关于x的方程 有两个实数根 , ,且 ,那么m的值为 .19. 如图,在平面直角坐标系中, , , .反比例函数 的图象经过平行四边形 的顶点 ,则 .
18. 关于x的方程 有两个实数根 , ,且 ,那么m的值为 .19. 如图,在平面直角坐标系中, , , .反比例函数 的图象经过平行四边形 的顶点 ,则 .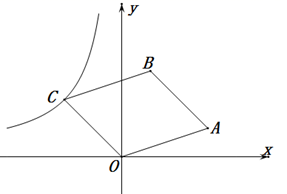 20. 如图,正方形 中,点 在边 上,点 在边 上,若 , ,则下列结论:① ;② ;③ ;④ ;其中结论正确的序号有 .
20. 如图,正方形 中,点 在边 上,点 在边 上,若 , ,则下列结论:① ;② ;③ ;④ ;其中结论正确的序号有 .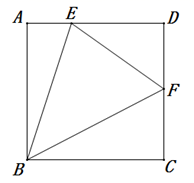
三、解答题
-
21. 防疫期间,全市所有学校都严格落实测体温进校园的防控要求.某校开设了A、B、C三个测温通道,某天早晨,该校小明和小丽两位同学将随机通过测温通道进入校园.(1)、小明从A测温通道通过的概率是;(2)、利用画树状图或列表的方法,求小明和小丽从同一个测温通道通过的概率.22. 某地计划对矩形广场进行扩建改造.如图,原广场长50m,宽40m,要求扩充后的矩形广场长与宽的比为3:2.扩充区域的扩建费用每平方米30元,扩建后在原广场和扩充区域都铺设地砖,铺设地砖费用每平方米100元.如果计划总费用642000元,扩充后广场的长和宽应分别是多少米?
 23. 如图,已知△ABC中,AB=BC=5,tan∠ABC= .
23. 如图,已知△ABC中,AB=BC=5,tan∠ABC= .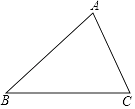 (1)、求边AC的长;(2)、设边BC的垂直平分线与边AB的交点为D,求 的值.
(1)、求边AC的长;(2)、设边BC的垂直平分线与边AB的交点为D,求 的值.
24. 如图,在正方形 中,点 在边 上,连接 ,作 于点 , 于点 ,连接 、 .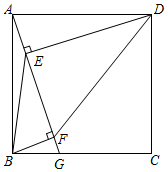 (1)、求证: ;(2)、设 , , ,求证: ;25. 如图,正比例函数y=kx(k≠0)的图象与反比例函数y=﹣ 的图象交于点A(n,2)和点B.
(1)、求证: ;(2)、设 , , ,求证: ;25. 如图,正比例函数y=kx(k≠0)的图象与反比例函数y=﹣ 的图象交于点A(n,2)和点B.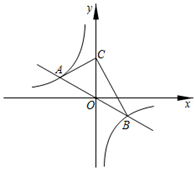 (1)、n= , k= ;(2)、点C在y轴正半轴上.∠ACB=90°,求点C的坐标;(3)、点P(m,0)在x轴上,∠APB为锐角,直接写出m的取值范围.26. 如图,在矩形 中, , ,点 , 分别为 , 的中点.
(1)、n= , k= ;(2)、点C在y轴正半轴上.∠ACB=90°,求点C的坐标;(3)、点P(m,0)在x轴上,∠APB为锐角,直接写出m的取值范围.26. 如图,在矩形 中, , ,点 , 分别为 , 的中点.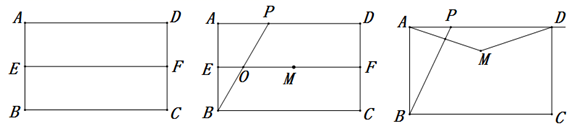 (1)、求证:四边形 是矩形;(2)、如图,点 是边 上一点, 交 于点 ,点 关于 的对称点为点 ,当点 落在线段 上时,则有 .请说明理由;(3)、如图,若点 是射线 上一个动点,点 关于 的对称点为点 ,连接 , ,当 是等腰三角形时,求 的长.
(1)、求证:四边形 是矩形;(2)、如图,点 是边 上一点, 交 于点 ,点 关于 的对称点为点 ,当点 落在线段 上时,则有 .请说明理由;(3)、如图,若点 是射线 上一个动点,点 关于 的对称点为点 ,连接 , ,当 是等腰三角形时,求 的长.