内蒙古霍林郭勒市初中联盟校2020-2021学年九年级上学期期末考试数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 下面的图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列成语中,表示不可能事件的是( )A、缘木求鱼 B、杀鸡取卵 C、探囊取物 D、日月经天,江河行地3. 如图,在平面直角坐标系中,以原点为圆心,半径为5的圆内有一点P(0,-3),那么经过点P的所有弦中,最短的弦的长为( )
2. 下列成语中,表示不可能事件的是( )A、缘木求鱼 B、杀鸡取卵 C、探囊取物 D、日月经天,江河行地3. 如图,在平面直角坐标系中,以原点为圆心,半径为5的圆内有一点P(0,-3),那么经过点P的所有弦中,最短的弦的长为( ) A、4 B、5 C、8 D、104. 如果在两个圆中有两条相等的弦,那么( )A、这两条弦所对的圆心角相等 B、这两条弦所对的弧相等 C、这两条弦都被与它垂直的半径平分 D、这两条弦所对的弦心距相等5. 一次围棋比赛,参赛的每两位棋手之间都要比赛一场,根据赛程计划共安排45场比赛,设本次比赛共有x个参赛棋手,则可列方程为( )A、 x(x﹣1)=45 B、 x(x+1)=45 C、x(x﹣1)=45 D、x(x+1)=456. 关于x的方程(m﹣3)x2﹣4x﹣2=0有两个不相等的实数根,则实数m的取值范围是( )A、m≥1 B、m>1 C、m≥1且m≠3 D、m>1且m≠37. 圆锥的底面半径是5cm,侧面展开图的圆心角是180°,圆锥的高是( )A、5 cm B、10cm C、6cm D、5cm8. 点 均在二次函数 的图象上,则 的大小关系是( )A、 B、 C、 D、9. 在同一平面直角坐标系中,一次函数 与二次函数 的图象可能是( )A、
A、4 B、5 C、8 D、104. 如果在两个圆中有两条相等的弦,那么( )A、这两条弦所对的圆心角相等 B、这两条弦所对的弧相等 C、这两条弦都被与它垂直的半径平分 D、这两条弦所对的弦心距相等5. 一次围棋比赛,参赛的每两位棋手之间都要比赛一场,根据赛程计划共安排45场比赛,设本次比赛共有x个参赛棋手,则可列方程为( )A、 x(x﹣1)=45 B、 x(x+1)=45 C、x(x﹣1)=45 D、x(x+1)=456. 关于x的方程(m﹣3)x2﹣4x﹣2=0有两个不相等的实数根,则实数m的取值范围是( )A、m≥1 B、m>1 C、m≥1且m≠3 D、m>1且m≠37. 圆锥的底面半径是5cm,侧面展开图的圆心角是180°,圆锥的高是( )A、5 cm B、10cm C、6cm D、5cm8. 点 均在二次函数 的图象上,则 的大小关系是( )A、 B、 C、 D、9. 在同一平面直角坐标系中,一次函数 与二次函数 的图象可能是( )A、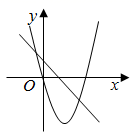 B、
B、 C、
C、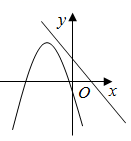 D、
D、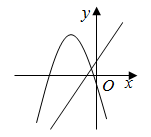
二、填空题
-
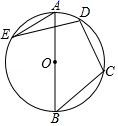
10. 如果点P(2,a)和点Q(-b,4)关于原点对称,则a-b= .11. 已知关于x的一元二次方程 的一个根是2,则此方程的另一个根是.12. 如图,AB 是⊙O 的直径,C,D,E 在⊙O 上,若∠AED=20°,则∠BCD 的度数为 .
 13. 已知二次函数的图象经过点 ,顶点为 将该图象向右平移,当它再次经过点 时,所得抛物线的函数表达式为.14. ⊙O的内接正三角形和外切正方形的边长之比是.15. 在围棋盒中有x颗白色棋子和若干颗黑色棋子,从盒中随机取出一颗棋子,取得白色棋子的概率是 ;如果再往盒中放进9颗黑色棋子,取得白色棋子的概率是 .则原来围棋盒中有白色棋子颗.16. 在平面直角坐标系中,抛物线y=x2的图象如图所示.已知A点坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1 , 过点A1作A1A2∥OA交抛物线于点A2 , 过点A2作A2A3∥x轴交抛物线于点A3 , 过点A3作A3A4∥OA交抛物线于点A4……,依次进行下去,则点A2019的坐标为 .
13. 已知二次函数的图象经过点 ,顶点为 将该图象向右平移,当它再次经过点 时,所得抛物线的函数表达式为.14. ⊙O的内接正三角形和外切正方形的边长之比是.15. 在围棋盒中有x颗白色棋子和若干颗黑色棋子,从盒中随机取出一颗棋子,取得白色棋子的概率是 ;如果再往盒中放进9颗黑色棋子,取得白色棋子的概率是 .则原来围棋盒中有白色棋子颗.16. 在平面直角坐标系中,抛物线y=x2的图象如图所示.已知A点坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1 , 过点A1作A1A2∥OA交抛物线于点A2 , 过点A2作A2A3∥x轴交抛物线于点A3 , 过点A3作A3A4∥OA交抛物线于点A4……,依次进行下去,则点A2019的坐标为 .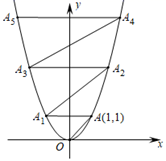
三、解答题
-
17. 解方程:(1)、 ;(2)、 .18. 汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2016年盈利1500万元,到2018年盈利2160万元,且从2016年到2018年,每年盈利的年增长率相同.(1)、求每年盈利的年增长率;(2)、若该公司盈利的年增长率继续保持不变,那么2019年该公司盈利能否达到2500万元?19. 一个不透明的布袋中装有2个黄球、4个红球和n(n 0)个蓝球,每个球除颜色外都相同.(1)、将布袋中的球搅匀后任意摸出一个球,记录其颜色后放回,重复该实验,经过大量实验后,发现摸到蓝球的频率稳定于0.8附近,那么n= ;(2)、若从布袋中取出一些球,只剩下2个黄球和2个红球,搅匀后任意摸出两个球,用列表或画树状图的方法求两次摸到球的颜色相同的概率.20. 某超市销售一种水果,进价为每箱40元,规定售价不低于进价.现在的售价为每箱72元,每月可销售60箱.经市场调查发现:若这种水果的售价每降低2元,则每月的销量将增加10箱,设每箱水果降价x元(x为偶数),每月的销量为y箱.(1)、写出y与x之间的函数关系式和自变量x的取值范围.(2)、若该超市在销售过程中每月需支出其他费用500元,则如何定价才能使每月销售水果的利润最大?最大利润是多少元?