内蒙古呼伦贝尔市莫力达瓦达斡尔族自治旗2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 下列图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. “任意买一张电影票,座位号是2的倍数”,此事件是( )A、不可能事件 B、随机事件 C、必然事件 D、确定事件4. 任意掷一枚质地均匀的骰子,掷出的点数大于4的概率是 ( )A、 B、 C、 D、5. 在平面直角坐标系中,P点关于原点的对称点为P1(﹣3,﹣ ),P点关于x轴的对称点为P2(a,b),则 等于( )A、2 B、﹣2 C、4 D、﹣46. 对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )A、开口向下 B、当x=-1,时,y有最大值是2 C、对称轴是x=-1 D、顶点坐标是(1,2)7. 如果关于x的一元二次方程k2x2﹣(2k+1)x+1=0有两个实数根,那么k的取值范围是( )A、k≥﹣ B、k≥﹣ 且k≠0 C、k<﹣ D、k>- 且k≠08.
3. “任意买一张电影票,座位号是2的倍数”,此事件是( )A、不可能事件 B、随机事件 C、必然事件 D、确定事件4. 任意掷一枚质地均匀的骰子,掷出的点数大于4的概率是 ( )A、 B、 C、 D、5. 在平面直角坐标系中,P点关于原点的对称点为P1(﹣3,﹣ ),P点关于x轴的对称点为P2(a,b),则 等于( )A、2 B、﹣2 C、4 D、﹣46. 对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )A、开口向下 B、当x=-1,时,y有最大值是2 C、对称轴是x=-1 D、顶点坐标是(1,2)7. 如果关于x的一元二次方程k2x2﹣(2k+1)x+1=0有两个实数根,那么k的取值范围是( )A、k≥﹣ B、k≥﹣ 且k≠0 C、k<﹣ D、k>- 且k≠08.如图,⊙O中,ABDC是圆内接四边形,∠BOC=110°,则∠BDC的度数是( )
 A、110° B、70° C、55° D、125°9. 边长为2的正六边形的边心距为( )A、1 B、2 C、 D、210. 一个滑轮起重装置如图所示,滑轮的半径是 ,当重物上升 时,滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度约为( )
A、110° B、70° C、55° D、125°9. 边长为2的正六边形的边心距为( )A、1 B、2 C、 D、210. 一个滑轮起重装置如图所示,滑轮的半径是 ,当重物上升 时,滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度约为( ) A、120° B、60° C、180° D、450°11. 在同一坐标系中,函数 与 的图象可能是( )A、
A、120° B、60° C、180° D、450°11. 在同一坐标系中,函数 与 的图象可能是( )A、 B、
B、 C、
C、 D、
D、 12. 如图,半圆O的直径AB=4,与半圆O内切的动圆O1与AB切于点M,设⊙O1的半径为y,AM=x,则y关于x的函数关系式是 ()
12. 如图,半圆O的直径AB=4,与半圆O内切的动圆O1与AB切于点M,设⊙O1的半径为y,AM=x,则y关于x的函数关系式是 ()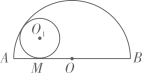 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 一个事件经过500次的试验,它的频率是0.32,那么它的概率估计值是 .14. 将抛物线y=﹣2x2向左平移1个单位,再向下平移3个单位得到的抛物线的解析式为 .15. 如图,从点P引⊙O的切线PA,PB,切点分别为A,B,DE切⊙O于C,交PA,PB于D,E.若△PDE的周长为20cm,则PA=cm.
 16. 如图,E,F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE,BF.将△ABE绕正方形的对角线交点O按顺时针方向旋转到△BCF,则旋转角是°.
16. 如图,E,F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE,BF.将△ABE绕正方形的对角线交点O按顺时针方向旋转到△BCF,则旋转角是°. 17. 如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=6cm.则图中阴影部分面积为cm2 .
17. 如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=6cm.则图中阴影部分面积为cm2 .
三、解答题
-
18. 解方程:(1)、3x(x+1)=3x+3.(2)、2x2+3x﹣1=0.19. 已知:如图,AB是⊙O的直径,AC为弦,P为AC延长线上一点,且AC=PC,PB的延长线交⊙O于D.求证:AC=DC.
 20. 如图,△ABC和△DEF关于某点对称
20. 如图,△ABC和△DEF关于某点对称 (1)、在图中画出对称中心O;(2)、连结AF、CD,判断四边形ACDF的形状,并说明理由.21. 将分别标有数字1、2、3的三张卡片洗匀后,背面朝上放在桌面上.(1)、若随机地抽取一张,则抽到数字恰好为1的概率是;(2)、请你通过列表或画树状图分析:先随机地抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,求组成的两位数能被4整除的概率.22. 甲型H1N1流感病毒的传染性极强,某地因1人患了甲型H1N1流感没有及时隔离治疗,经过两天传染后共有9人患了甲型H1N1流感,每天传染中平均一个人传染了几个人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型H1N1流感?
(1)、在图中画出对称中心O;(2)、连结AF、CD,判断四边形ACDF的形状,并说明理由.21. 将分别标有数字1、2、3的三张卡片洗匀后,背面朝上放在桌面上.(1)、若随机地抽取一张,则抽到数字恰好为1的概率是;(2)、请你通过列表或画树状图分析:先随机地抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,求组成的两位数能被4整除的概率.22. 甲型H1N1流感病毒的传染性极强,某地因1人患了甲型H1N1流感没有及时隔离治疗,经过两天传染后共有9人患了甲型H1N1流感,每天传染中平均一个人传染了几个人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型H1N1流感?
23. 如图,隧道的横截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线的解析式为 。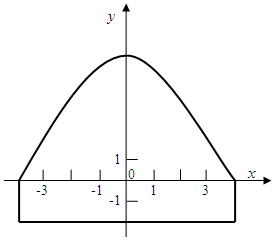 (1)、一辆货运车车高4m,宽2m,它能通过该隧道吗?(2)、如果该隧道内设双行道,中间遇车间隙为0.4m,那么这辆卡车是否可以通过?
(1)、一辆货运车车高4m,宽2m,它能通过该隧道吗?(2)、如果该隧道内设双行道,中间遇车间隙为0.4m,那么这辆卡车是否可以通过?

