内蒙古巴彦淖尔市乌拉特前旗2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 计算:( )﹣1+tan30°·sin60°=( )A、﹣ B、2 C、 D、2. 一元二次方程 配方后可化为( )A、 B、 C、 D、3. 如图,一把梯子靠在垂直水平地面的墙上,梯子 的长是3米.若梯子与地面的夹角为 ,则梯子顶端到地面的距离BC为( )
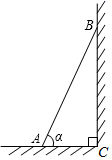 A、 米 B、 米 C、 米 D、 米4. 如图, 是 的直径, 是弦,点 在直径 的两侧.若 , ,则 的长为( )
A、 米 B、 米 C、 米 D、 米4. 如图, 是 的直径, 是弦,点 在直径 的两侧.若 , ,则 的长为( ) A、 B、 C、 D、5. 如图,在 中, , , 为 边上的一点,且 .若 的面积为 ,则 的面积为( )
A、 B、 C、 D、5. 如图,在 中, , , 为 边上的一点,且 .若 的面积为 ,则 的面积为( )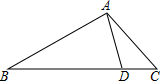 A、 B、 C、 D、6. 在同一平面直角坐标系内,二次函数 与一次函数 的图象可能是( )A、
A、 B、 C、 D、6. 在同一平面直角坐标系内,二次函数 与一次函数 的图象可能是( )A、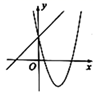 B、
B、 C、
C、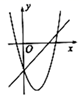 D、
D、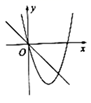 7. 如图, 的直径 垂直于弦 ,垂足为 , , ,则 的长为( )
7. 如图, 的直径 垂直于弦 ,垂足为 , , ,则 的长为( ) A、2.5 B、4 C、5 D、108. 如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( )
A、2.5 B、4 C、5 D、108. 如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( ) A、 B、 C、 D、9. 在平面直角坐标系中,对于二次函数 ,下列说法中错误的是( )A、 的最小值为1 B、图象顶点坐标为(2,1),对称轴为直线 C、当 时, 的值随 值的增大而增大,当 时, 的值随 值的增大而减小 D、它的图象可以由 的图象向右平移2个单位长度,再向上平移1个单位长度得到10. 如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则 的值为( )
A、 B、 C、 D、9. 在平面直角坐标系中,对于二次函数 ,下列说法中错误的是( )A、 的最小值为1 B、图象顶点坐标为(2,1),对称轴为直线 C、当 时, 的值随 值的增大而增大,当 时, 的值随 值的增大而减小 D、它的图象可以由 的图象向右平移2个单位长度,再向上平移1个单位长度得到10. 如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则 的值为( ) A、1 B、 C、 -1 D、 +111. 若一元二次方程x2﹣7x+5=0的两个实数根分别是a、b,则一次函数y=abx+a+b的图象一定不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限12. 如图,已知二次函数 ( )的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:①当x>3时,y<0;②3a+b<0;③ ;④ ;其中正确的结论是( )
A、1 B、 C、 -1 D、 +111. 若一元二次方程x2﹣7x+5=0的两个实数根分别是a、b,则一次函数y=abx+a+b的图象一定不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限12. 如图,已知二次函数 ( )的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:①当x>3时,y<0;②3a+b<0;③ ;④ ;其中正确的结论是( )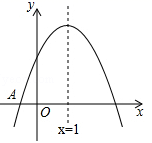 A、①③④ B、①②③ C、①②④ D、①②③④
A、①③④ B、①②③ C、①②④ D、①②③④二、填空题
-
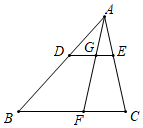
13. 已知 是二次函数,则m= .14. 如图,在△ABC中,DE∥BC,交AB于点D,交AC于点E,点F为BC边上一点,AF与DE交于点G.若 ,则 .
 15. 已知关于x的一元二次方程 有两个不相等的实数根,则k的取值范围是 .16. 如图,在△ABC中,AB=AC,∠ABC=45°,以AB为直径的⊙O交BC于点D,若BC=4 cm,则图中阴影部分的面积为 .
15. 已知关于x的一元二次方程 有两个不相等的实数根,则k的取值范围是 .16. 如图,在△ABC中,AB=AC,∠ABC=45°,以AB为直径的⊙O交BC于点D,若BC=4 cm,则图中阴影部分的面积为 . 17. 一个扇形的弧长是20πcm,面积是240πcm2 , 则这个扇形的圆心角是度.18. 如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是 .
17. 一个扇形的弧长是20πcm,面积是240πcm2 , 则这个扇形的圆心角是度.18. 如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是 .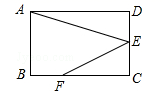 19. 如图,PA,PB是圆O的切线,切点为A、B,∠P=50°,点C是圆O上异于A,B的点,则∠ACB等于 .
19. 如图,PA,PB是圆O的切线,切点为A、B,∠P=50°,点C是圆O上异于A,B的点,则∠ACB等于 .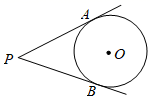 20. 如图, 的对角线 交于点 , 平分 交 于点 ,交 于点 ,且 ,连接 .下列结论:① ;② ;③ ;④ .其中正确的结论有(填写所有正确结论的序号)
20. 如图, 的对角线 交于点 , 平分 交 于点 ,交 于点 ,且 ,连接 .下列结论:① ;② ;③ ;④ .其中正确的结论有(填写所有正确结论的序号)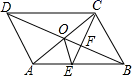
三、解答题
-
21. 在△ABC中,BC=2,AB=2 ,AC=b,且关于x的方程x2﹣4x+b=0有两个相等的实数根,求AC边上的中线长及∠A的度数.22. 如图,已知:Rt△ABC中,∠ACB=90°,点E为AB上一点,AC=AE=3,BC=4,过点A作AB的垂线交射线EC于点D , 延长BC交AD于点F .
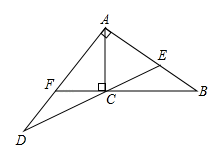 (1)、求CF的长;(2)、求∠D的正切值.23. 一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2 .
(1)、求CF的长;(2)、求∠D的正切值.23. 一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2 .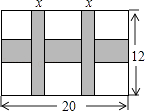 (1)、求y与x之间的函数关系式;(2)、若图案中三条彩条所占面积是图案面积的 ,求横、竖彩条的宽度.24. 如图, 是 的直径,点 是弧 上一点,且 , 与 交于点 .
(1)、求y与x之间的函数关系式;(2)、若图案中三条彩条所占面积是图案面积的 ,求横、竖彩条的宽度.24. 如图, 是 的直径,点 是弧 上一点,且 , 与 交于点 . (1)、求证: 是 的切线;(2)、若 平分 ,求证: ;(3)、在(2)的条件下,延长 , 交于点 ,若 , ,求 的长.25. 如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(1)、求证: 是 的切线;(2)、若 平分 ,求证: ;(3)、在(2)的条件下,延长 , 交于点 ,若 , ,求 的长.25. 如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m. (1)、求抛物线的解析式和直线BC的解析式;(2)、当点P在线段OB上运动时,求线段MN的最大值;(3)、当点P在线段OB上运动时,若△CMN是以MN为腰的等腰直角三角形时,求m的值;(4)、当以C、O、M、N为顶点的四边形是平行四边形时,直接写出m的值.
(1)、求抛物线的解析式和直线BC的解析式;(2)、当点P在线段OB上运动时,求线段MN的最大值;(3)、当点P在线段OB上运动时,若△CMN是以MN为腰的等腰直角三角形时,求m的值;(4)、当以C、O、M、N为顶点的四边形是平行四边形时,直接写出m的值.