江苏省苏州市高新区新区二中2021年数学中考二模试卷

试卷更新日期：2021-11-09 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列四个图标中，轴对称图案为（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $3 a^{2} + 2 a^{3} = 5 a^{5}$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 $a^{3} \div a^{2} = a$

查看试题解析
3. 某班体育委员调查了本班学生一周的体育锻炼时间，统计数据如下表所示：

锻炼时间（小时）

7

8

9

10

11

学生人数

6

9

10

8

7

则该班学生一周的体育锻炼时间的众数和中位数分别是（）

A、9，9.5 B、9，9 C、8，9 D、8，9.5

查看试题解析
4. 2020年12月11日“双 $12$ 苏州购物节”火爆启动，截止12月12日 $20 : 00$ 苏州地区线上消费支付实时金额达到了 $8460211211$ 元人民币，用科学记数法表示 $8460211211$ （精确到 $100000000$ ）为（）

A、 $85 \times 10^{8}$ B、 $8.46 \times 10^{10}$ C、 $8.46 \times 10^{9}$ D、 $8.5 \times 10^{9}$

查看试题解析
5. 定义：等腰三角形的一个底角与其顶角的度数的比值 $k (k > 1)$ 称为这个等腰三角形的“优美比”．若在等腰三角形 $A B C$ 中， $∠ A = 36 °,$ 则它的优美比 $k$ 为（）

A、 $\frac{3}{2}$ B、 $2$ C、 $\frac{5}{2}$ D、 $3$

查看试题解析
6. 下列整数中，与 $\sqrt{5} - 1$ 最接近的是（）

A、-1 B、0 C、1 D、2

查看试题解析
7. 如图，为了测量某建筑物MN的高度，在平地上A处测得建筑物顶端M的仰角为30°，向N点方向前进16m到达B处，在B处测得建筑物顶端M的仰角为45°，则建筑物MN的高度等于（）

A、 $8 (\sqrt{3} + 1)$ m B、 $8 (\sqrt{3} - 1)$ m C、 $16 (\sqrt{3} + 1)$ m D、 $16 (\sqrt{3} - 1)$ m

查看试题解析
8. 在数轴上，点A表示－2，点B表示4，P、Q为数轴上两点，点P从点A出发以每秒1个单位长度的速度向左运动，同时点Q从点B出发以每秒2个单位长度的速度向左运动，点Q到达原点O后，立即以原来的速度返回，当点Q回到点B时，点P与点Q同时停止运动.设点P运动的时间为x秒，点P与点Q之间的距离为y个单位长度，则下列图象中表示y与x的函数关系的是是（）

A、 B、 C、 D、

查看试题解析
9. 如图5，在反比例函数 $y = - \frac{2}{x}$ 的图象上有一动点 $A$ ，连接 $A O$ 并延长交图象的另一支于点 $B$ ，在第一象限内有一点C，满足 $A C = B C$ ，当点 $A$ 运动时，点 $C$ 始终在函数 $y = \frac{k}{x}$ 的图象上运动，若 $\tan ∠ C A B = 2$ ，则 $k$ 的值为（）

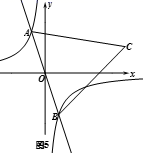A、2 B、4 C、6 D、8

查看试题解析
10. 如图，边长为2的菱形纸片ABCD中，∠A=60°，将纸片折叠，点A、D分别落在A′、D′处，且A′D′经过点B，EF为折痕，当D′F⊥CD时，CF的值为（）

A、 $\sqrt{3} - 1$ B、 $2 \sqrt{3} - 2$ C、 $\frac{\sqrt{3}}{2}$ D、 $4 - 2 \sqrt{3}$

查看试题解析

二、填空题

11. 下列4个数： $0. \overset{•}{1} \overset{•}{3}$ ， $\frac{7}{3}$ ，π﹣3.14， $\sqrt{5}$ ，其中无理数有个.

查看试题解析
12. 已知a²﹣4b²=12，且a﹣2b=﹣3，则a+2b= ．

查看试题解析
13. 一组数据1，2，a，4，5的平均数是3，则这组数据的方差为．

查看试题解析
14. 将一张扇形纸片围成一个圆锥.若扇形的半径是 $5cm$ ，弧长是 $6 π cm$ ，则这个圆锥的高是 $cm$ .

查看试题解析
15. 如果关于x的一元二次方程 $k^{2} x^{2} - (2 k + 1) x + 1 = 0$ 有两个不相等的实数根，那么 $k$ 的取值范围是.

查看试题解析
16. 如图，在 $Δ A B C$ 中， $∠ B A C = 90 ° ，$ 点 $D$ 在 $B C$ 上， $B D = B A$ ，点 $E$ 在 $B C$ 的延长线上， $C A = C E$ ，连接 $A E$ ，则 $∠ D A E$ 的度数为 $^{\circ}$ .

查看试题解析
17. 如图，已知点 $A$ ，点 $B$ 分别为 $y$ 轴和 $x$ 轴正半轴上两点，以 $A B$ 为斜边作等腰直角三角形 $A B C$ ，点 $A$ ，点 $B$ ，点 $C$ 按顺时针方向排列，若 $A B = 4 ， Δ A O B$ 的面积为 $3$ ，则点 $C$ 的坐标为.

查看试题解析
18. 如图，在Rt△ABC中，∠ACB=90°，BC=6，AC=8.点D、E分别是边AB、BC的中点，连接DE，将△BDE绕点B按顺时针方向旋转一定角度（这个角度小于90°）后，点D的对应点D′和点E的对应点E′以及点A三个点在一直线上，连接CE′，则CE′=.

查看试题解析

三、解答题

19. 计算： ${(\sqrt{2} - 3)}^{0} - \sqrt{9} + \sqrt[3]{- 8}$

查看试题解析
20. 解不等式组 ${\begin{array}{l} 3 (x - 1) < 5 x + 1 \\ \frac{1}{2} x - 1 \leq 7 - \frac{3}{2} x \end{array}$

查看试题解析
21. 某技工培训中心有钳工 $20$ 名、车工 $30$ 名．现将这 $50$ 名技工派往 $A, B$ 两地工作，设派往 $A$ 地 $x$ 名钳工，余下的技工全部派往 $B$ 地，两地技工的月工资情况如下表：

钳工/（元/月）

车工/（元/月）

$A$ 地

$3600$

$3200$

$B$ 地

$3200$

$2800$

(1)、试写出这 $50$ 名技工的月工资总额 $y$ （元）与 $x$ （名）之间的函数表达式，并写出 $x$ 的取值范围；

(2)、根据预算，这 $50$ 名技工的月工资总额不得超过 $155000$ 元．当派往 $A$ 地多少名钳工时，这些技工的月工资总额最大？月工资总额最大为多少元？

查看试题解析
22. 随着交通道路的不断完善，带动了旅游业的发展，某市某旅游景区有A、B、C、D、E等著名景点，该市旅游部门统计绘制出2018年“十·一”长假期间旅游情况统计图，根据以下信息解答下列问题：

(1)、2018年“十·一”期间，该市此旅游景区共接待游客万人，扇形统计图中A景点所对应的圆心角的度数是；

(2)、补全条形统计图；

(3)、根据近几年到该市旅游人数增长趋势，预计2019年“十·一”节将有80万游客选择该市旅游，请估计有多少万人会选择去E景点旅游？

查看试题解析
23. “共和国勋章”是中华人民共和国的最高荣誉勋章，在2019年获得“共和国勋章”的八位杰出人物中，有于敏、孙家栋、袁隆平、黄旭华四位院士，如图是四位院士（依次记为 $A 、 B 、 C 、 D$ ）为让同学们了解四位院士的贡献，老师设计如下活动：取四张完全相同的卡片，分别写上 $A 、 B 、 C 、 D$ 四个标号，然后背面朝上放置，搅匀后每个同学可以从中随机抽取一张，记下标号后放回，老师要求每位同学依据抽到的卡片上的标号查找相应院士的资料制作小报，求小明和小华查找同一位院士资料的概率.请用画树状图或列表法加以说明，并列举所用等可能的结果.

查看试题解析
24. 如图1，在四边形 $A B C D$ 中，若 $∠ A ， ∠ C$ 均为直角，则称这样的四边形为“美妙四边形”.

(1)、概念理解：长方形美妙四边形（填“是”或“不是”）；

(2)、性质探究：如图l，试证明： $C D^{2} - A B^{2} = A D^{2} - B C^{2}$ ；

(3)、概念运用：如图2，在等腰直角三角形 $A B C$ 中， $A B = A C ， ∠ A = 90 °$ ，点 $D$ 为 $B C$ 的中点，点 $E$ ，点 $F$ 分别在 $A B ， A C$ 上，连接 $D E ， D F$ ，如果四边形 $A E D F$ 是美妙四边形，试证明： $A E + A F = A B$ .

查看试题解析
25. 如图，用 $x$ 表示 $A$ 中的实数， $y$ 表示 $B$ 中与 $x$ 对应的实数，且 $y$ 与 $x$ 满足一次函数 $y = k x + b (k ， b$ 为常数， $k \neq 0$ ）.

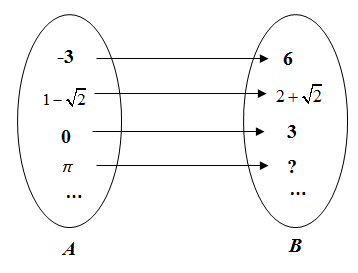(1)、 $π$ 是 $A$ 中的实数，则 $B$ 中与之对应的实数是；

(2)、点 $(a^{2} + 1 ， 2 - a^{2})$ 在该函数的图象上吗？请说明理由；

(3)、若点 $P (a ， 2 a - 3)$ 到直线 $y = k x + b$ 的距离是 $\sqrt{2}$ ，求 $a$ 的值.

查看试题解析
26. 在 $Δ A B C$ 中， $A B = A C ，$ 点 $P$ 为 $Δ A B C$ 边上的动点，速度为 $1 c m / s$ .

(1)、如图1，点 $D$ 为 $A B$ 边上一点， $A D = 1 c m$ ，动点 $Р$ 从点 $D$ 出发，在 $Δ A B C$ 的边上沿 $D \to B \to C$ 的路径匀速运动，当到达点 $C$ 时停止运动.设 $Δ A P C$ 的面积为 $S_{1} (c m^{2}) ， Δ B P C$ 的面积为 $S_{2} (c m^{2})$ ，点 $P$ 运动的时间为 $t (s) . S_{1} ， S_{2}$ 与 $t$ 之间的函数关系如图2所示，根据题意解答下列问题：
①在图1中， $A B =$ ▲ $c m ， B C =$ ▲ $c m$ ；

②在图2中，求 $E F$ 和 $M N$ 的交点 $H$ 的坐标；

(2)、在（1）的条件下，如图3，若点 $P$ ，点 $Q$ 同时从点 $A$ 出发，在 $Δ A B C$ 的边上沿 $A \to B \to C$ 的路径匀速运动，点 $Q$ 运动的速度为 $0.5 c m / s$ ，当点 $Р$ 到达点 $C$ 时，点 $P$ 与点 $Q$ 同时停止运动.求 $t$ 为何值时， $| B P - B Q |$ 最大？最大值为多少？

查看试题解析
27. 如图，已知 $A B$ 是⊙ $O$ 的直径，且 $A B = 4$ ，点 $C$ 在半径 $O A$ 上(点 $C$ 与点 $O$ 、点 $A$ 不重合)，过点 $C$ 作 $A B$ 的垂线交⊙ $O$ 于点 $D$ . 连接 $O D$ ，过点 $B$ 作 $O D$ 的平行线交⊙ $O$ 于点 $E$ ，交 $C D$ 的延长线于点 $F$ .

(1)、若点 $E$ 是弧BD的中点，求 $∠ F$ 的度数；

(2)、求证： $B E = 2 O C$ ；

(3)、设 $A C = x$ ，则当 $x$ 为何值时 $B E \cdot E F$ 的值最大? 最大值是多少?

查看试题解析
28. 如图①已知抛物线 $y = a x^{2} - 3 a x - 4 a$ $(a < 0)$ 的图象与 $x$ 轴交于 $A$ 、 $B$ 两点（ $A$ 在 $B$ 的左侧），与 $y$ 的正半轴交于点 $C$ ，连结 $B C$ ；二次函数的对称轴与 $x$ 轴的交点 $E$ .

(1)、抛物线的对称轴与 $x$ 轴的交点 $E$ 坐标为，点 $A$ 的坐标为.

(2)、若以 $E$ 为圆心的圆与 $y$ 轴和直线 $B C$ 都相切，试求出抛物线的解析式：

(3)、在（2）的条件下，如图② $Q (m ， 0)$ 是 $x$ 的正半轴上一点，过点 $Q$ 作 $y$ 轴的平行线，与直线 $B C$ 交于点 $M$ 与抛物线交于点 $N$ ，连结 $C N$ ，将 $△ C M N$ 沿 $C N$ 翻折， $M$ 的对应点为 $M$ ’，在图②中探究：是否存在点 $Q$ ，使得 $M$ ’恰好落在 $y$ 轴上？若存在，请求出 $Q$ 的坐标：若不存在，请说明理由.

查看试题解析

	钳工/（元/月）	车工/（元/月）
$A$ 地	$3600$	$3200$
$B$ 地	$3200$	$2800$

锻炼时间（小时）	7	8	9	10	11
学生人数	6	9	10	8	7