河南省邓州市2021年数学中招一模试卷

试卷更新日期：2021-11-09 类型：中考模拟

进入出卷网下载

一、单选题

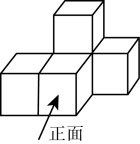
1. 下列各数中，比 $- 1$ 小的数是（）

A、 $| - 2 |$ B、 ${(- 2)}^{- 1}$ C、0 D、-2

查看试题解析
2. 如图，是由五个相同的小立方体搭成的几何体，这个几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列调查中，最适宜采用普查方式的是（）

A、调查黄河水中的泥沙含量 B、了解我市中学生的睡眠情况 C、调查全国中学生视力和用眼卫生情况 D、检查我国即将发射的“神舟十二号载人飞船”各零部件的情况

查看试题解析
4. 将一副三角板（∠A=∠FDE=90°，∠F=45°，∠C=60°，点D在边AB上）按图中所示位置摆放，两条斜边为EF，BC，且 $E F / / B C$ ，则 $∠ A D E$ 等于（）

A、 $135 °$ B、 $145 °$ C、 $165 °$ D、 $170 °$

查看试题解析
5. 目前代表华为手机最强芯片的麒麟990处理器采用7nm工艺制造，已知1nm=10⁻³um，1um=10⁻³mm，则7nm等于（）

A、 $7 \times 10^{- 3} mm$ B、 $7 \times 10^{- 5} mm$ C、 $7 \times 10^{- 6} mm$ D、 $7 \times 10^{- 7} mm$

查看试题解析
6. 若点 $A (x_{1} ， - 5) ， B (x_{2} ， 2) ， C (x_{3} ， 5)$ 都在反比例函数 $y = \frac{10}{x}$ 的图象上，则 $x_{1} ， x_{2} ， x_{3}$ 的大小关系是（）

A、 $x_{1} < x_{2} < x_{3}$ B、 $x_{2} < x_{3} < x_{1}$ C、 $x_{1} < x_{3} < x_{2}$ D、 $x_{3} < x_{1} < x_{2}$

查看试题解析
7. 直线 $y = x + a$ 不经过第二象限，则关于 $x$ 的方程 $a x^{2} + 2 x + 1 = 0$ 实数解的个数是（）.

A、0个 B、1个 C、2个 D、1个或2个

查看试题解析
8. 我国古代数学名著《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何?”意思是：用一根绳子去量一根木条，绳子还剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条长多少尺?如果设木条长x尺，绳子长y尺，那么可列方程组为（）

A、 ${\begin{cases} y = x + 4.5 \\ 0.5 y = x - 1 \end{cases}$ B、 ${\begin{cases} y = x + 4.5 \\ y = 2 x - 1 \end{cases}$ C、 ${\begin{cases} y = x - 4.5 \\ 0.5 y = x + 1 \end{cases}$ D、 ${\begin{cases} y = x - 4.5 \\ y = 2 x - 1 \end{cases}$

查看试题解析
9. 如图，在菱形ABCD中，按以下步骤作图：①分别以点C和点D为圆心，大于 $\frac{1}{2} C D$ 的同样的长为半径作狐，两弧交于M，N两点；②作直线MN，交CD于点E，连接BE.若直线MN恰好经过点A，则下列说法错误的是（）

A、 $∠ A B C = 60 °$ B、 $\tan ∠ A B E = \frac{\sqrt{3}}{2}$ C、 $S_{△ A B E} = 2 S_{△ A D E}$ D、若 $A B = 4$ ，则 $B E = 4 \sqrt{7}$

查看试题解析
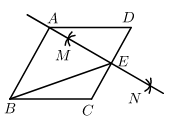10. 如图，矩形ABCD的顶点A，B分别在x轴，y轴上， $O A = O B = 2 ， A D = 4 \sqrt{2}$ ，将矩形ABCD绕点O顺时针旋转，每次旋转 $90 °$ ，则第2021次旋转结束时，点C的坐标为（）

A、 $(4 ， 6)$ B、 $(6 ， 4)$ C、 $(- 6 ， 4)$ D、 $(- 4 ， 6)$

查看试题解析

二、填空题

11. 计算： $| - 2 | - \sqrt[3]{8}$ = ．

查看试题解析
12. 不等式组 ${\begin{array}{l} 2 x + 1 \geq 0 \\ 1 - \frac{1}{2} x > 0 \end{array}$ 的最大整数解为.

查看试题解析
13. 一个不透明的袋子里有4个小球，上面分别标有数字-2，-1，1，2，小球除所标数字不同外，其它完全相同，摇匀后摸出一球，记下数字为a，不放回，再摸出一球，记下数字为b，若点M的坐标为 $(a ， b)$ 则点M落在双曲线 $y = \frac{- 2}{x}$ 上的概率为.

查看试题解析
14. 如图，AB是 $⊙ O$ 的直径，且 $A B = 10$ ，过点O作 $O C ⊥ A B$ 交 $⊙ O$ 于点C， $∠ C A D = 30 °$ ，点P是直径AB上的动点，求PC，PD， $\overset{⌢}{C D}$ 所围成的图形周长最小值.

查看试题解析
15. 如图，正方形ABCD和正方形EFCG边长分别为3和1，点F，G分别在边BC，CD上，P为AE的中点，连PF，则PF的长为.

查看试题解析

三、解答题

16. 先化简，再求值（ $\frac{3}{m + 2}$ +m﹣2）÷ $\frac{m^{2} - 2 m + 1}{m + 2}$ ；其中m＝ $\sqrt{2}$ +1.

查看试题解析

17. 某校为了解学生对我国社会主义现代化建设中“两个一百年”奋斗目标的知晓情况，对全校学生进行了相关知识测试（满分为100分），并从七、八年级各随机抽取了10名同学的成绩，收集数据为：

七年级：90，95，95，80，90，80 ，85，90，85，100

八年级：85，85，95，80，95，90，90，90，100，90

整理数据：

	80	85	90	95	100
七年级	2	2	3	2	1
八年级	1	2	a	2	1

分析数据：

	平均数	中位数	众数	方差
七年级	89	b	90	39
八年级	90	90	c	30

根据以上信息回答下列问题：

(1)、请直接写出表格中a，b，c的值；

(2)、通过数据分析，你认为哪个年级的成绩比较好？请说明理由；

(3)、该校七、八年级共有600人，本次测试成绩不低于90分的为“优秀”，估计这两个年级共有多少名学生达到“优秀”.

查看试题解析

18. 如图，在 $△ A B C$ 中， $A B = A C$ ，BC为 $⊙ O$ 的直径，D为 $⊙ O$ 上任意一点，连接AD交BC于点F，过A作 $E A ⊥ A D$ 交DB的延长线于E，连接CD.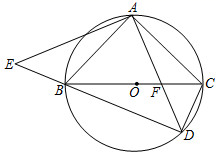

(1)、求证： $B E = C D$

(2)、填空：①当 $∠ E A B =$ $°$ 时，四边形ABDC是正方形
②若四边形ABDC的面积为6，则AD的长为.

查看试题解析
19. 邓州杏山地质公园位于河南省邓州市西南约50公里处，紧邻丹江口水库南水北调渠首，面积32.5平方公里.公园地质景观及自然景观为原始状态，是一座集岩溶地貌、典型底层剖面和地质构造为主，水体为辅、人文和生态相互辉映的综合性公园（如图1）.双休日期间，小明携带测量工具随妈妈到杏山地质公园游览，为测量杏山主峰的高度，如图2，小明在坡角为 $30 ° (∠ C D E = 30 °)$ 的斜坡C处测得峰顶A的仰角为 $31 °$ ，沿斜坡CD走 $80m$ 到平坦地面上点D处，测得峰顶A的仰角为 $45 °$ .

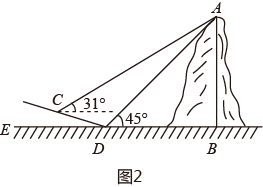(1)、求主峰到地面的高度AB（结果保留整数，参考数据 $\sin 31 ° \approx 0.5 ， \cos 31 ° \approx 0.9 ， \tan 31 ° \approx 0.6 \sqrt{3} \approx 1.73$ ）

(2)、妈妈借助手机某项功能得到杏山主峰海拔为 $469m$ ，所测水平地面的海拔为 $263m$ ，请你算出小明测量主峰高度的误差，并帮助他提一条减小误差的方法.

查看试题解析
20. 共享电动车是一种新理念下的交通工具，主要面向 $3 ~ 10 km$ 的出行市场现有A、B品牌的共享电动车，收费与骑行时间之间的函数关系如图所示，其中A品牌收费方式对应 $y_{1}$ ，B品牌的收费方式对应 $y_{2}$ .

(1)、请求出两个函数关系式，并说明B品牌的收费方案.

(2)、如果小明每天早上需要骑行A品牌或B品牌的共享电动车去工厂上班，已知两种品牌共享电动车的平均行驶速度均为 $20 km / h$ ，小明家到工厂的距离为 $6 km$ ，那么小明选择哪个品牌的共享电动车更省钱呢？

(3)、直接写出第几分钟，两种收费相差1.5元.

查看试题解析
21. 如图，抛物线 $y = a x^{2} + b x + c$ 过 $(1 ， 0)$ ， $(3 ， 0)$ ， $(0 ， 6)$ 三点，边长为4的正方形 $O A B C$ 的顶点 $A$ ， $C$ 分别在 $x$ 轴上， $y$ 轴上.

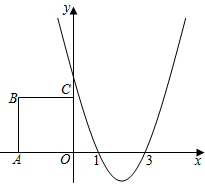(1)、求抛物线解析式，并直接写出当 $- 1 \leq x \leq 4$ 时 $y$ 的最大值与最小值的差.

(2)、将正方形 $O A B C$ 向右平移，平移距离记为 $h$ .
①当点 $C$ 首次落在抛物线上，求 $h$ 的值.

②当抛物线落在正方形内的部分，满足 $y$ 随 $x$ 的增大而减小时，请直接写出 $h$ 的取值范围.

查看试题解析

22. 如图，在形OAB中，

∠ A O B = 90 ° ， B O = 10 cm

，C是半径BO上一动点，过点B作AC的垂线交线段AC的延长线于点D，交线段AO的延长线于点E，连接DO.明明发现，随着点C位置的改变，

△ O D E

的三边都随之改变，所以，明明决定以BC的长度为自变量，设BC的长为

x cm

，借助学习函数的经验来研究

△ O D E

三边的变化规律，请你将下面的探究过程补充完整.

(1)、根据点C在OB上的不同位置，画出相应的图形，测量线段OD，DE的长度，得到下表的几组对应值.

$B C / cm$	0.0	1.0	2.0	3.0	4.0	5.0	6.0	7.0	8.0	9.0	10.0
$O D / cm$	a	9.7	8.8	8.1	7.3	6.3	5.3	4.1	2.8	1.4	0
$D E / cm$	14.1	12.7	11.2	9.8	8.2	6.7	5.2	3.7	2.4	1.1	0

①上表中a的值为 ▲ ；

②OE与自变量BC的长度具有某种关系，所以无需测量OE，通过推理并计算可以得到，请说明理由.

(2)、在同一平面直角坐标系

x O y

中，以BC的长为x，OD的长为

y_{1}

，DE的长为

y_{2}

，如图，已经画出了

y_{2}

的函数图象，请你描点并画出

y_{1}

的函数图象.

(3)、结合函数图象，请直接写出以下问题的答案.（结果保留一位小数）

①当 $O D = D E$ 时，BC的长度约为.

②当 $△ O D E$ 的三边中某一边的长度为 $9 cm$ 时，BC的长度约为.

查看试题解析

23. 等腰△ABC，AB=AC，∠BAC=120°，AF⊥BC于F，将腰AB绕点A逆时针旋转至AB′，记旋转角为α，连接BB′，过C作CE垂直于直线BB′，垂足为E，连接CB′.

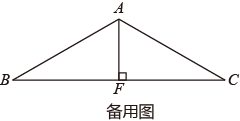(1)、问题发现：如图1，当 $α = 40 °$ 时， $∠ C B^{'} E$ 的度数为；连接EF，则 $\frac{E F}{A B^{'}}$ 的值为.

(2)、拓展探究：当 $0 ° < α < 360 °$ ，且 $α \neq 120 °$ 时，
①（1）中的两个结论是否仍然成立？如果成立，请仅就图2的情形进行证明；如果不成立，请说明理由；

②解决问题：当A，E，F三点共线时，请直接写出 $\frac{B B^{'}}{B E}$ 的值.

查看试题解析