辽宁省葫芦岛市建昌县2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 下列图形是中心对称图形的是( )A、
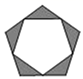 B、
B、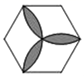 C、
C、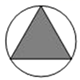 D、
D、 2. 下列说法中错误的是( )A、不可能事件发生的概率为0 B、概率很小的事不可能发生 C、必然事件发生的概率是1 D、随机事件发生的概率大于0、小于13. 一元二次方程 的根的情况是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法判断4. 做随机抛掷一枚硬币的实验,下面有三个推断:①当抛掷次数是100时,若“正面向上”的次数是47,则“正面向上”的概率一定是0.47;②随着实验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;③抛掷次数为150时,“正面向上”的频率一定是0.45,其中合理的是( )A、① B、② C、①② D、①③5. 一元二次方程 配方后可变形为( )A、 B、 C、 D、6. 如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和 的长分别为( )
2. 下列说法中错误的是( )A、不可能事件发生的概率为0 B、概率很小的事不可能发生 C、必然事件发生的概率是1 D、随机事件发生的概率大于0、小于13. 一元二次方程 的根的情况是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法判断4. 做随机抛掷一枚硬币的实验,下面有三个推断:①当抛掷次数是100时,若“正面向上”的次数是47,则“正面向上”的概率一定是0.47;②随着实验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;③抛掷次数为150时,“正面向上”的频率一定是0.45,其中合理的是( )A、① B、② C、①② D、①③5. 一元二次方程 配方后可变形为( )A、 B、 C、 D、6. 如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和 的长分别为( )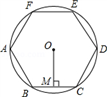 A、2, B、2 ,π C、 , D、2 ,7. 某钢铁厂一月份生产钢铁560吨,从二月份起,由于改进操作技术,使得第一季度共生产钢铁1850吨,问二、三月份平均每月的增长率是多少?若设二、三月份平均每月的增长率为x,则可得方程( )A、 B、 C、 D、8. 如图,AB是⊙O的弦,OC⊥AB,交⊙O于点C,连接OA,OB,BC,若∠ABC=20°,则∠BAO的度数是( )
A、2, B、2 ,π C、 , D、2 ,7. 某钢铁厂一月份生产钢铁560吨,从二月份起,由于改进操作技术,使得第一季度共生产钢铁1850吨,问二、三月份平均每月的增长率是多少?若设二、三月份平均每月的增长率为x,则可得方程( )A、 B、 C、 D、8. 如图,AB是⊙O的弦,OC⊥AB,交⊙O于点C,连接OA,OB,BC,若∠ABC=20°,则∠BAO的度数是( )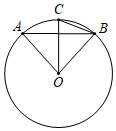 A、40° B、45° C、50° D、55°9. 已知点A(x1 , y1),B(x2 , y2)是双曲线 上的两点,若x2<0<x1 , 则有( )A、0<y1<y2 B、0<y2<y1 C、y2<0<y1 D、y1<0<y210. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=﹣1,与x轴的交点为(x1 , 0)、(x2 , 0),其中0<x1<1,有下列结论:①c>0;②﹣3<x2<﹣2;③a+b+c<0;④b2﹣4ac>0;⑤已知图象上点A(4,y1),B(1,y2),则y1>y2 . 其中,正确结论的个数有( )
A、40° B、45° C、50° D、55°9. 已知点A(x1 , y1),B(x2 , y2)是双曲线 上的两点,若x2<0<x1 , 则有( )A、0<y1<y2 B、0<y2<y1 C、y2<0<y1 D、y1<0<y210. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=﹣1,与x轴的交点为(x1 , 0)、(x2 , 0),其中0<x1<1,有下列结论:①c>0;②﹣3<x2<﹣2;③a+b+c<0;④b2﹣4ac>0;⑤已知图象上点A(4,y1),B(1,y2),则y1>y2 . 其中,正确结论的个数有( ) A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题
-
11. 一个不透明的盒子中装有6个红球,3个黄球和1个绿球,这些球除了颜色外无其他差别,从中随机摸出一个小球,则摸到的不是红球的概率为
12. 一元二次方程x2=x的解为 .13. 点P(3,-2)关于原点对称的点的坐标是 .14. 关于x的一元二次方程 有两个不相等的实数根,k的取值范围是 .15. 如图, 的半径为5,AB为 的弦,OC⊥AB于点C,若OC=3,则AB的长为 .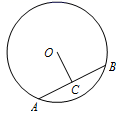 16. 抛物线 向上平移1个单位后,再向右平移2个单位,得到的抛物线的解析式为 .17. 鸡瘟是一种传播速度很快的传染病,一轮传染为一天时间,某养鸡场于某日发现一例,两天后发现共有169只鸡患有这种病.若每例病鸡传染健康鸡的只数均为x只,则可列方程为 .18. 二次函数 的函数图象如图,点A0位于坐标原点,点A1 , A2 , A3 , A4 , …在 轴的正半轴上,点B1 , B2 , B3 , B4 , …在二次函数 位于第一象限的图象上,△A0B1A1 , △A1B2A2 , △A2B3A3 , △A3B4A4…,都是直角顶点在抛物线上的等腰直角三角形,则△A10B11A11的斜边长为 .
16. 抛物线 向上平移1个单位后,再向右平移2个单位,得到的抛物线的解析式为 .17. 鸡瘟是一种传播速度很快的传染病,一轮传染为一天时间,某养鸡场于某日发现一例,两天后发现共有169只鸡患有这种病.若每例病鸡传染健康鸡的只数均为x只,则可列方程为 .18. 二次函数 的函数图象如图,点A0位于坐标原点,点A1 , A2 , A3 , A4 , …在 轴的正半轴上,点B1 , B2 , B3 , B4 , …在二次函数 位于第一象限的图象上,△A0B1A1 , △A1B2A2 , △A2B3A3 , △A3B4A4…,都是直角顶点在抛物线上的等腰直角三角形,则△A10B11A11的斜边长为 .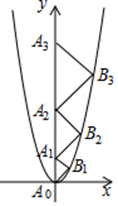
三、解答题
-
19. 对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.(1)、甲组抽到A小区的概率是多少(2)、请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.20. 如图,在平面直角坐标系中,△OAB的三个顶点的坐标分别为O(0,0)A(5,3),B(0,5).
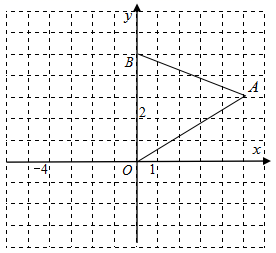 (1)、画出△OAB绕原点O逆时针方向旋转90°后得到的△OA1B1;(2)、∠OAA1=;(3)、求旋转过程中,线段OB扫过的图形的面积.21. 如图,一次函数 的图象与反比例函数 的图象交于A,B两点,其中A(﹣2,1).
(1)、画出△OAB绕原点O逆时针方向旋转90°后得到的△OA1B1;(2)、∠OAA1=;(3)、求旋转过程中,线段OB扫过的图形的面积.21. 如图,一次函数 的图象与反比例函数 的图象交于A,B两点,其中A(﹣2,1).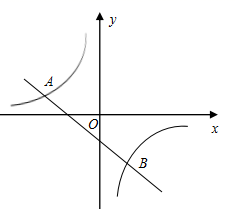 (1)、求反比例函数和一次函数的解析式;(2)、求△AOB的面积;(3)、根据图象直接写出使一次函数值大于反比例函数值的x的取值范围.22. 如图,有一面积为150平方米的矩形花圃,花圃的一边靠墙(墙长18米),另三边用竹篱笆围成.如果竹篱笆的长为35米,求矩形花圃的长和宽各是多少米?
(1)、求反比例函数和一次函数的解析式;(2)、求△AOB的面积;(3)、根据图象直接写出使一次函数值大于反比例函数值的x的取值范围.22. 如图,有一面积为150平方米的矩形花圃,花圃的一边靠墙(墙长18米),另三边用竹篱笆围成.如果竹篱笆的长为35米,求矩形花圃的长和宽各是多少米? 23. 如图,AB为⊙O的直径,点C在⊙O上,∠ACB的平分线与AB交于点E,与⊙O交于点D,P为AB延长线上一点,且∠PCB=∠PAC.
23. 如图,AB为⊙O的直径,点C在⊙O上,∠ACB的平分线与AB交于点E,与⊙O交于点D,P为AB延长线上一点,且∠PCB=∠PAC.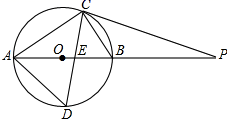 (1)、试判断直线PC与⊙O的位置关系,并说明理由.(2)、若AC=8,BC=6,求⊙O的半径及AD的长.24. 某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.(1)、直接写出y与x之间的函数关系式;(2)、当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?(3)、若该网店每星期想要获得6480元的利润,求每件童装售价应为多少元?25. 已知在矩形ABCD中,∠ADC的平分线DE与BC交于点E,点P是线段DE上一定点(其中EP<PD)
(1)、试判断直线PC与⊙O的位置关系,并说明理由.(2)、若AC=8,BC=6,求⊙O的半径及AD的长.24. 某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.(1)、直接写出y与x之间的函数关系式;(2)、当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?(3)、若该网店每星期想要获得6480元的利润,求每件童装售价应为多少元?25. 已知在矩形ABCD中,∠ADC的平分线DE与BC交于点E,点P是线段DE上一定点(其中EP<PD)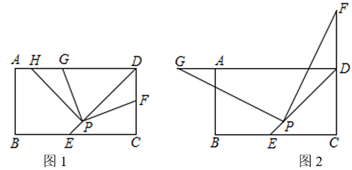 (1)、如图1,若点F在CD边上(不与C,D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD,PF分别交射线DA于点H,G.
(1)、如图1,若点F在CD边上(不与C,D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD,PF分别交射线DA于点H,G.①直接写出PG与PF之间的数量关系;
②猜想DF,DG,DP的数量关系,并证明你的结论.
(2)、如图2,若点F在CD的延长线上(不与D重合),将PF绕点P逆时针旋转90°,交射线DA于点G,判断(1)②中DF,DG,DP之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请直接写出它们所满足的数量关系式.26. 如图1,抛物线 与x轴交于A(2,0),B(4,0),D为抛物线的顶点.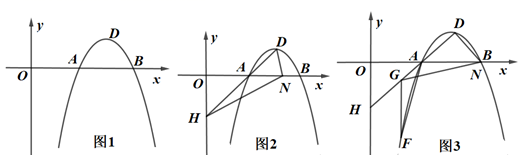 (1)、求抛物线的解析式;(2)、如图2,若H为射线DA与y轴的交点,N为射线AB上一点,设N点的横坐标为t,△DHN的面积为S,求S与t的函数关系式;(3)、如图3,在(2)的条件下,若N与B 重合,G为线段DH上一点,过G作y轴的平行线交抛物线于F,连接AF,若∠AGN=∠FAG,求GF的长.
(1)、求抛物线的解析式;(2)、如图2,若H为射线DA与y轴的交点,N为射线AB上一点,设N点的横坐标为t,△DHN的面积为S,求S与t的函数关系式;(3)、如图3,在(2)的条件下,若N与B 重合,G为线段DH上一点,过G作y轴的平行线交抛物线于F,连接AF,若∠AGN=∠FAG,求GF的长.