浙江省杭州市三校2021-2022学年九年级上学期数学第一次联考试卷

试卷更新日期：2021-11-09 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列函数表达式中，一定为二次函数的是（）

A、y＝3x-1 B、y＝ax²+bx+c C、y＝2x²-2x+1 D、y＝x²-（x-1）²

查看试题解析
2. 对于抛物线y＝（x﹣1）²﹣2，下列说法正确的是（　　）

A、开口向下 B、对称轴是直线x＝﹣1 C、顶点坐标（﹣1，﹣2） D、与x轴有交点

查看试题解析
3. 在一个不透明的袋中装有2个黄球和2个红球，它们除颜色外没有其他区别，从袋中任意摸出一个球，然后放加搅匀，再从袋中任意摸一个球，那么两次都摸到黄球的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
4. 某小组作“用频率估计概率的实验时，统计了某一结果出现的频率，绘制了如图所示的折线统计图，则符合这一结果的实验最有可能的是（）

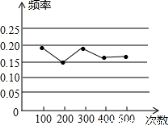A、掷一个质地均匀的正六面体骰子，向上的面点数是4 B、一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃 C、暗箱中有1个红球和2个黄球，它们只有颜色上的区别，从中任取一球是黄球 D、在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀”

查看试题解析
5. 甲、乙两人各自掷一个普通的正方体骰子，如果两者之和为偶数，甲得1分；如果两者之和为奇数，乙得1分，此游戏（）

A、是公平的 B、对乙有利 C、对甲有利 D、以上都不对

查看试题解析
6. 已知二次函数y＝﹣4（x﹣1）²+k的图象上有三点A（ $\sqrt{2}$ ，y₁），B（﹣2，y₂），C（5，y₃），则y₁、y₂、y₃的大小关系为（　　）

A、y₁＞y₂＞y₃ B、y₂＞y₁＞y₃ C、y₃＞y₁＞y₂ D、y₃＞y₂＞y₁

查看试题解析
7. 把抛物线y＝2(x﹣1)²+3先向右平移3个单位，再向上平移1个单位，得到的抛物线的解析式是（　　）

A、y＝2(x+2)²+4 B、y＝2(x﹣4)²+4 C、y＝2(x+2)²+2 D、y＝2(x﹣4)²+2

查看试题解析
8. 如图，已知顶点为（﹣3，﹣6）的抛物线y＝ax²+bx+c经过点（﹣1，﹣4），则下列结论中正确的是（　　）

A、b²﹣4ac＜0 B、ax²+bx+c≥﹣6 C、若点（﹣2，m），（﹣4，n）在抛物线上，则m＞n D、关于x的一元二次方程ax²+bx+c＝﹣4的两根为﹣6和﹣1

查看试题解析
9. 已知抛物线y＝ax²+bx+c的图象如图所示，下列结论①a﹣b+c＜0；②b²﹣4ac＞0；③b＜1；④2a+b＞0；⑤a+c+1＞0.正确的是（　　）

A、①②④⑤ B、①②③④ C、②③④⑤ D、①②③⑤

查看试题解析
10. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $∠ A = 60 °$ ， $A B = 8$ .点P是 $A B$ 边上的一个动点，过点P作 $P D ⊥ A B$ 交直角边于点D，设 $A P$ 为x， $△ A P D$ 的面积为y，则下列图象中，能表示y与x的函数关系的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 一天晚上，小伟帮妈妈清洗茶杯，三个茶杯只有颜色不同，其中一个无盖，突然停电了，小伟只好把杯盖与茶杯随机地搭配在一起，则花色完全搭配正确的概率是.

查看试题解析
12. 把大小和形状完全相同的4张卡片分成两组，每组2张，分别标上1，2，将这两组卡片分别放入两个盒子中搅匀，再从中各随机抽取一张，则取出的两张卡片数字之和为奇数的概率＝.

查看试题解析
13. 如图，图2是图1的拱形大桥的示意图.桥拱与桥面的交点为O，B，以点O为原点，水平直线OB为x轴，建立平面直角坐标系，桥的拱形可以近似看成抛物线y $= - \frac{1}{400}$ （x﹣80）²+16，桥拱与桥墩AC的交点C恰好在水面上，AC⊥x轴.若OA＝20米，则桥面离水面的高度AC为

查看试题解析
14. 现有一“祥云”零件剖面图，如图所示，它由一个半圆和左右两支抛物线的一部分组成，且关于y轴对称.其中半圆交y轴于点E，直径 $A B = 2$ ， $O E = 2$ ；两支抛物线的顶点分别为点A、点B.与x轴分别交于点C、点D；直线BC的解析式为： $y = k x + \frac{3}{4}$ .则零件中BD这段曲线的解析式为.

查看试题解析
15. 有五张正面分别写有数字-4，-3，0，2，3的卡片，五张卡片除了数字不同外其余全部相同，现将它们背面朝上，洗匀后从中随机抽取一张，记卡片上的数字为n，则抽取的n既能使关于x的方程 $x^{2} - 2 (n + 1) x + n (n - 3) = 0$ 有实数根，又能使以x为自变量的二次函数 $y = - x^{2} + 2 n x + 1$ ，当 $x > 2$ 时，y随x的增大而减小的概率为.

查看试题解析
16. 定义[a，b，c]为函数y＝ax²＋bx＋c的特征数，下面给出特征数[2m，1﹣m，﹣1﹣m]的函数的一些相关结论：①当m＝﹣2时，抛物线的顶点为（ $\frac{3}{8}$ ， $\frac{25}{16}$ ）；②当m≠0时，函数图象恒过定点；③当m＜0时，函数在x＜1时，y随x的增大而减小；④当m＞0时，函数图象截x轴所得的线段的长度大于 $\frac{3}{2}$ .其中正确的结论是（直接填正确结论的编号）.

查看试题解析

三、解答题

17. 北京世界园艺博览会为满足大家的游览需求，倾情打造了4条各具特色的游完路线，如下表：

A

B

C

D

漫步世园会

爱家乡，爱园艺

清新园艺之旅

车览之旅

小美和小红都计划去世园会游玩，她们各自在这4条路线中任意选择一条，每条线路被选择的可能性相同.

(1)、求小美选择路线“清新园艺之旅”的概率是多少？

(2)、用画树状图或列表的方法，求小美和小红恰好选择同一条路线的概率.

查看试题解析
18. 不透明袋子中装有红、绿小球各一个，除颜色外无其他差别.随机摸出一个小球后，放回并摇匀，再随机摸出一个.求下列事件的概率：

(1)、第一次摸到红球，第二次摸到绿球；

(2)、两次都摸到相同颜色的小球；

(3)、两次摸到的球中一个绿球、一个红球.

查看试题解析
19. 某二次函数图象上部分点的横坐标x，纵坐标y的对应值如表：

x

0

1

2

3

4

y

m

0

1

0

﹣3

(1)、求此二次函数的解析式；

(2)、表格中的m＝；

(3)、此抛物线上有两点P（x₁ ， y₁）Q（x₂ ， y₂），x₁＜2，x₂＞2，若x₁+x₂＞4，则y₁y₂.

查看试题解析
20. 如图，钢球从斜面顶端由静止开始沿斜面滚下，速度每秒增加 $1.5 m / s$ .

(1)、写出滚动的距离s（单位：m）关于滚动的时间t（单位：s）的函数解析式.（提示：本题中，距离=平均速度 $\bar{v} \times$ 时间t， $\bar{v} = \frac{v_{0} + v_{t}}{2}$ ，其中， $v_{0}$ 是开始时的速度， $v_{t}$ 是t秒时的速度.）

(2)、如果斜面的长是 $3 m$ ，钢球从斜面顶端滚到底端用多长时间？

查看试题解析
21. 某地区在2020年开展脱贫攻坚的工作中大力种植有机蔬菜.某种蔬菜的销售单价与销售月份之间的关系如图（1）所示，每千克成本与销售月份之间的关系如图（2）所示.（其中图（1）的图象是直线，图（2）的图象是抛物线，其最低点坐标是（6，1））.

(1)、求每千克蔬菜销售单价y与销售月份x之间的关系式；

(2)、判断哪个月份销售每千克蔬菜的收益最大？并求最大收益；

(3)、求出一年中销售每千克蔬菜的收益大于1元的月份有哪些？

查看试题解析
22. “田忌赛马”的故事闪烁着我国古代先贤的智慧光芒.该故事的大意是：齐王有上、中、下三匹马 $A_{1} ， B_{1} ， C_{1}$ ，田忌也有上、中、下三匹马 $A_{2} ， B_{2} ， C_{2}$ ，且这六匹马在比赛中的胜负可用不等式表示如下： $A_{1} > A_{2} > B_{1} > B_{2} > C_{1} > C_{2}$ （注： $A > B$ 表示A马与B马比赛，A马获胜）.一天，齐王找田忌赛马，约定：每匹马都出场比赛一局，共赛三局，胜两局者获得整场比赛的胜利.面对劣势，田忌事先了解到齐王三局比赛的“出马”顺序为上马、中马、下马，并采用孙膑的策略：分别用下马、上马、中马与齐王的上马、中马、下马比赛，即借助对阵（ $C_{2} A_{1} ， A_{2} B_{1} ， B_{2} C_{1}$ ）获得了整场比赛的胜利，创造了以弱胜强的经典案例.
假设齐王事先不打探田忌的“出马”情况，试回答以下问题：

(1)、如果田忌事先只打探到齐王首局将出“上马”，他首局应出哪种马才可能获得整场比赛的胜利？并求其获胜的概率；

(2)、如果田忌事先无法打探到齐王各局的“出马”情况，他是否必败无疑？若是，请说明理由；若不是，请列出田忌获得整场比赛胜利的所有对阵情况，并求其获胜的概率.

查看试题解析
23. 在平面直角坐标系中，二次函数y=ax²+bx+3的图象经过点M(1−m，n)，点N(m+ $\frac{3}{a}$ ，n)，交y轴于点A.

(1)、求a，b满足的关系式；

(2)、若抛物线上始终存在不重合的P，Q两点（P在Q的左边）关于原点对称.
①求证：a<0；

②若点A，P，Q三点到直线l：y=− $\frac{9}{4}$ x+ $\frac{3}{2}$ 的距离相等，求线段PQ长.

查看试题解析

A	B	C	D
漫步世园会	爱家乡，爱园艺	清新园艺之旅	车览之旅

x	0	1	2	3	4
y	m	0	1	0	﹣3