四川师大一中锦江校区2021-2022学年九年级上学期数学9月月考试卷

试卷更新日期：2021-11-09 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、x²＋x²＝2x⁴ B、x²·x⁴＝x⁸ C、(－x²)³＝－x⁶ D、x⁹÷x³＝x³

查看试题解析
2. 下列倡导节约的图案中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列是一元一次方程的是（）

A、 $x^{2} - 2 x - 3 = 0$ B、 $2 x + y = 5$ C、 $\frac{x}{2} + \frac{1}{x} = 1$ D、 $x + 1 = 0$

查看试题解析
4. 如图，l₁ $/ /$ l₂ $/ /$ l₃ ，直线a，b与l₁ ， l₂ ， l₃分别相交于A，B，C和D，E，F.若 $\frac{A B}{B C} = \frac{2}{5}$ ，DE＝4，则EF的长为（　　）

A、10 B、 $\frac{20}{3}$ C、12 D、14

查看试题解析
5. 正十边形的外角和为（）

A、180° B、360° C、720° D、1440°

查看试题解析
6. 若 $\frac{y}{x} = \frac{2}{5}$ ，则 $\frac{x + y}{x}$ 的值为（　　）

A、 $\frac{2}{7}$ B、 $\frac{5}{7}$ C、 $\frac{7}{5}$ D、 $\frac{7}{2}$

查看试题解析
7. 如图，菱形ABCD中，对角线AC，BD相交于点O，点M是DC的中点.若菱形ABCD的周长为24，则 $O M$ 的长为（）

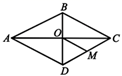A、12 B、8 C、6 D、3

查看试题解析
8. 世界文化遗产“三孔”景区已经完成5G基站布设，“孔夫子家”自此有了5G 网络.5G网络峰值速率为4G 网络峰值速率的10倍，在峰值速率下传输500兆数据，5G 网络比4G 网络快45秒，求这两种网络的峰值速率．设4G网络的峰值速率为每秒传输 $x$ 兆数据，依题意，可列方程是（）

A、 $\frac{500}{x} - \frac{500}{10 x} = 45$ B、 $\frac{500}{10 x} - \frac{500}{x} = 45$ C、 $\frac{5000}{x} - \frac{500}{x} = 45$ D、 $\frac{500}{x} - \frac{5000}{x} = 45$

查看试题解析
9. 如图，每个小正方形边长均为1，则下列图中的三角形（阴影部分）与左图中△ABC相似的是（）

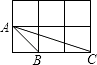A、 B、 C、 D、

查看试题解析
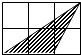10. 如图，在平面直角坐标系中， $△$ ABC的顶点A在第一象限，点B，C的坐标分别为(2，1)，(6，1)，∠BAC＝90°，AB＝AC，直线AB交y轴于点P，若 $△$ ABC与 $△ A^{'} B^{'} C^{'}$ 关于点P成中心对称，则点 $A^{'}$ 的坐标为（　　）

A、(﹣4，-5) B、(﹣5，﹣4) C、(﹣3，﹣4) D、(﹣4，﹣3)

查看试题解析

二、填空题

11. 四条线段a、b、c、d成比例，其中b=3，c=2，d=6，那么a=.

查看试题解析
12. 如图，身高 $1.6 m$ 的小华站在距路灯5m的C点处，测得她在灯光下的影长CD为 $2.5 m$ ，则路灯的高度 $A E$ 为.

查看试题解析
13. 在1：2000000的地图上量得甲、乙两地间的距离为6厘米，那么，甲、乙两地间的实际距离是米.（结果用科学记数法表示）

查看试题解析
14. 如图，菱形ABCD中，分别以点C、D为圆心，大于 $\frac{1}{2}$ CD长为半径作弧，两弧分别交于点E、F，作直线EF，且直线EF恰好经过点A，与边CD交于点M.连接BM，若AB＝6，则BM＝.

查看试题解析
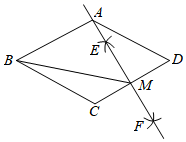15. 设a，b是方程x²+x﹣2021＝0的两个实数根，则（a+1）（b+1）的值为.

查看试题解析
16. 如图，在黄金矩形ABCD中，四边形ABFG、GHED均为正方形， $\frac{A B}{A D} = \frac{C E}{D E}$ ，现将矩形ABCD沿AE向上翻折，得四边形 $A E C^{'} B^{'}$ ，连接BB′，若AB＝2，则线段 $B B^{'}$ 的长度为.

查看试题解析
17. 如图，矩形ABCD中，AB＝2，BC＝3，点E，F分别在边AB，边BC上运动，点G在矩形内，且DG⊥CG，EF⊥FG，FG：EF＝1：2，则线段GF的最小值为.

查看试题解析
18. 如图，AC是平行四边形ABCD的对角线，且AC⊥AB，在AD上截取AH＝AB，连接BH交AC于点F，过点C作CE平分∠ACB交BH于点G，且GF＝2 $\sqrt{2}$ ，CG＝6，则AC＝.

查看试题解析

三、解答题

19. 解方程

(1)、x²﹣10x+16＝0；

(2)、2x²﹣3x﹣4＝0.

查看试题解析
20. 先化简，再求值： $(\frac{a^{2} + 4}{a} - 4) \div (1 - \frac{2}{a})$ ，其中 $a = \sqrt{2} + 2$

查看试题解析
21. 某校为了解学生对中国民族乐器的喜爱情况，随机抽取了本校的部分学生进行调查（每名学生选择并且只能选择一种喜爱乐器），现将收集到的数据绘制如下的两幅不完整的统计图.

(1)、这次共抽取学生进行调查，扇形统计图中的 $x =$ .

(2)、请补全统计图；

(3)、在扇形统计图中“扬琴”所对扇形的圆心角是度；

(4)、若该校有3000名学生，请你估计该校喜爱“二胡”的学生约有名.

查看试题解析
22. 在矩形ABCD中，E为DC边上一点，把 $△ A D E$ 沿AE翻折，使点D恰好落在BC边上的点F ．

(1)、求证： $△ A B F \sim △ F C E$ ；

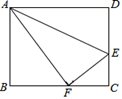(2)、若AB＝2 $\sqrt{3}$ ，AD＝4，求EC的长．

查看试题解析
23. 如图，要利用一面墙（墙长为25米）建一个矩形场地，用100米的围栏围成三个大小相同的矩形，设矩形的边长AB为x米，矩形场地的总面积为y平方米.

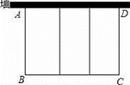(1)、请用含有x的式子表示y（不要求写出x的取值范围）；

(2)、当x为何值时，矩形场地的总面积为400平方米？

查看试题解析
24. 在正方形ABCD中，点E在边AD上，连接CE，点F在CE上，过点F作GH⊥CE分别交AB、CD于G、H两点.

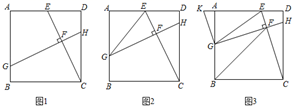(1)、如图1，求证：DE＝CH﹣BG；

(2)、如图2，连接EG，若EC平分∠DEG，求证：FE＝FH；

(3)、在（2）的条件下，如图3，过点G作GK $/ /$ CE交DA的延长线于点K，连接BF，若AK＝DH，GE＝10，求线段BF的长.

查看试题解析
25. 2020年秋冬以来，由于全国大葱种植面积的减少与产量的减产，10月份到12月份，大葱的批发价格持续走高。10月份大葱的批发价格为5元/公斤，12月份大葱的批发价格涨到7.2元/公斤．

(1)、求10月份到12月份大葱批发价格的月平均增长率；

(2)、进入12月份以来，某农贸市场按照7.2元/公斤的批发价购进大葱进行销售，销售价格为10元/公斤，每天能销售大葱500公斤，为了扩大销售，增加盈利，最大限度让利于顾客，该农贸市场决定对大葱进行降价销售，根据市场调查发现，大葱的销售单价每降低0.1元，每天的销售量将增加40公斤，求当大葱的销售价格降低多少元时，该农贸市场每天销售大葱的利润为1640元？

查看试题解析
26. 如图，在Rt $△$ ABC中，AC＝BC＝6，∠ACB＝90°，正方形BDEF的边长为2 $\sqrt{2}$ ，将正方形BDEF绕点B旋转一周，连接AE、BE、CF.

(1)、如图1所示，求证 $△$ ABE∼ $△$ CBF，并直接写出 $\frac{A E}{C F}$ 的值；

(2)、在正方形BDEF绕点B旋转过程中，当A、E、F三点共线时，求CF的长；

(3)、如图2所示，在正方形BDEF旋转过程中，设AE的中点为M，连接FM，请直接写出FM长度的最大值.

查看试题解析
27. 在平面直角坐标系中，直线y＝﹣3x﹣ $\frac{5}{2}$ 交x轴于点A，交y轴于点B，直线y＝﹣ $\frac{3}{4}$ x+3交x轴于点C，交y轴于点D.

(1)、如图1，连接BC，求 $△$ BCD的面积；

(2)、如图2，在直线y＝﹣ $\frac{3}{4}$ x+3上存在点E，使得∠ABE＝45°，求点E的坐标；

(3)、如图3，在（2）的条件下，连接OE，过点E作CD的垂线交y轴于点F，点P在直线EF上，在平面中存在一点Q，使得以OE为一边，O，E，P，Q为顶点的四边形为菱形，请直接写出点Q的坐标.

查看试题解析