辽宁省丹东市2020-2021学年九年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 某几何体的三视图如图所示，该几何体是（）

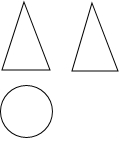A、圆锥 B、圆柱 C、三棱锥 D、球

查看试题解析
2. 一元二次方程 $x^{2} + 3 x = 0$ 的根是（）

A、 $x_{1} = x_{2} = 3$ B、 $x_{1} = x_{2} = - 3$ C、 $x_{1} = 3$ ， $x_{2} = 0$ D、 $x_{1} = - 3$ ， $x_{2} = 0$

查看试题解析

3. 某班的一个数学兴趣小组为了考察本市某条斑马线上驾驶员礼让行人的情况，每天利用放学时间进行调查，下表是该小组一个月内累计调查的结果，由此结果可估计驾驶员能主动给行人让路的概率为（）

抽查车辆数	100	500	1000	2000	3000	4000
能礼让的驾驶员人数	95	486	968	1940	2907	3880
能礼让的频率	0.95	0.972	0.968	0.97	0.969	0.97

A、0.95 B、0.96 C、0.97 D、0.98

查看试题解析

4. 下面是一天中四个不同时刻两座建筑物的影子，将它们按时间先后顺序正确的是（　　）

A、③①④② B、③②①④ C、③④①② D、②④①③

查看试题解析
5. 顺次连接对角线互相垂直的四边形各边中点，所得到的四边形一定是（）

A、正方形 B、矩形 C、菱形 D、以上都不对

查看试题解析
6. 在反比例函数 $y = \frac{k}{x} (k < 0)$ 的图像上有 $A (- 3 ， y_{1})$ ， $B (- 1 ， y_{2})$ ， $C (2 ， y_{3})$ 三个点，则下列各式中正确的是（）

A、 $y_{1} < y_{3} < y_{2}$ B、 $y_{3} < y_{1} < y_{2}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
7. 如图，在 $△ A B C$ 中， $D E / / B C$ ，若 $A D = 4$ ， $B D = 8$ ，则 $△ A D E$ 与四边形 $D E C B$ 的面积比为（）

A、 $1 ： 3$ B、 $1 ： 4$ C、 $1 ： 8$ D、 $1 ： 9$

查看试题解析
8. 如图，在 $Rt △ A B C$ 和 $Rt △ A B D$ 中， $∠ A C B = ∠ A D B = 90 °$ ， $A B = 10$ ， $M$ 是 $A B$ 的中点，连接 $M C$ ， $M D$ ， $C D$ ，若 $C D = 6$ ，则 $△ M C D$ 的面积为（）

A、12 B、12.5 C、15 D、24

查看试题解析
9. 如图，在正方形 $A B C D$ 中， $E$ ， $F$ ， $G$ 分别是 $A B$ ， $B C$ ， $C D$ 上的动点，且 $B E = C F = D G$ ，连接 $E F$ ， $F G$ ， $E G$ ，连接 $B D$ 分别交 $E G$ ， $E F$ 于点 $M$ ， $N$ ．有以下结论：① $△ E B F ≌ △ F C G$ ；② $E G = \sqrt{2} E F$ ；③点 $A$ ， $M$ ， $C$ 在同一条直线上；④若 $A E = \frac{1}{3} A B$ ，则 $B N = \frac{3}{8} B M$ ．其中正确的结论有（）个

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

10. 已知 $\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = 2$ ，且 $b + d + f \neq 0$ ，若 $a + c + e = 12$ ，则 $b + d + f =$ ．

查看试题解析
11. 将 $3 x^{2} - 2 x - 2 = 0$ 配方成 ${(x + m)}^{2} = n$ 的形式，则 $n =$ ．

查看试题解析
12. 点 $C$ 是线段 $A B$ 的黄金分割点，且 $A C < B C$ ，若 $A B = 20 c m$ ，则 $B C =$ $c m$ ．

查看试题解析
13. 某企业年初受疫情影响，第一季度的销售额为400万元，由于我国控制疫情措施得力，该企业第二、三季度销售额连续增长，第三季度销售额达到了900万元，则二、三季度的平均增长率为．

查看试题解析
14. 关于x的一元二次方程（k-2）x²-4x-3=0有两个不相等的实数根，则k的取值范围是.

查看试题解析
15. 菱形 $A B C D$ 周长为 $52 c m$ ，它的一条对角线长为 $10 c m$ ，则另一条对角线长为 $c m$ ．

查看试题解析
16. 在平面直角坐标系中， $△ A B C$ 的三个顶点坐标分别为 $A (- 2 ， 4)$ ， $B (- 3 ， 1)$ ， $C (- 2 ， 0)$ ，以原点 $O$ 为位似中心，把 $△ A B C$ 缩小为原来的 $\frac{1}{2}$ ，得到 $△ A^{'} B^{'} C^{'}$ ，则点 $A$ 的对应点 $A^{'}$ 的坐标为．

查看试题解析
17. 如图，在平面直角坐标系中，矩形 $O A B C$ 的两边 $O A$ ， $O C$ 落在坐标轴上，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象分别交 $B C$ ， $O B$ 于点 $D$ ， $E$ ，且 $\frac{B D}{C D} = \frac{5}{4}$ ，若 $S_{△ A O E} = 15$ ，则 $k$ 的值为．

查看试题解析
18. 如图，在平面直角坐标系中，矩形 $O A B C$ 的顶点 $A$ 和 $C$ 分别在 $x$ 轴和 $y$ 轴上，点 $B$ 的坐标为 $(8 ， 10)$ ，点 $E$ 为边 $B C$ 上一动点，连接 $O E$ ，将 $△ O C E$ 沿 $O E$ 折叠，点 $C$ 落在点 $C^{'}$ 处，当 $△ C^{'} C B$ 为直角三角形时，直线 $O C^{'}$ 的解析式为．

查看试题解析

三、解答题

19. 解方程

(1)、 $5 x + 2 = 3 x^{2}$

(2)、 ${(2 x - 1)}^{2} = {(3 x - 4)}^{2}$

查看试题解析
20. 下面已给出了几何体的主视图，请补画出该几何体的左视图和俯视图

查看试题解析
21. 为了增强学生体质，开展体育娱乐教学，某校举行了“趣味运动会”，运动会的比赛项目有：“两人三足”、“春种秋收”、“有轨电车”、“摸石过河”（分别用字母 $A$ ， $B$ ， $C$ ， $D$ 依次表示这四个运动项目），将 $A$ ， $B$ ， $C$ ， $D$ 这四个字母分别写在4张完全相同的不透明卡片的正面上，把这4张卡片背面朝上洗匀后放在桌面上．小明和小亮参加趣味比赛，比赛时小明先从中随机抽取一张卡片，记录下卡片上的内容，放回后洗匀，再由小亮从中随机抽取一张卡片，选手按各自抽取的卡片上内容进行趣味运动比赛．

(1)、小明参加“有轨电车”的概率是；

(2)、请用列表法或画树状图法，求出小明和小亮参加同一项目的概率．

查看试题解析
22. 某商场销售一款消毒用湿巾，这款消毒用湿巾的成本价为每包6元，当销售单价定为10元时，每天可售出80包，根据市场行情，现决定降价销售，市场调研反映：销售单价每降低0.5元，则每天可多售出20包，为使每天这种消毒湿巾的利润达到360元，商场应把这种消毒湿巾降价多少元？

查看试题解析
23. 如图， $A D$ 是 $Δ A B C$ 的中线， $A E / / B C$ ，且 $A E = \frac{1}{2} B C$ ，连接 $D E$ ， $C E$ ．

(1)、求证： $A B = D E$ ；

(2)、当 $Δ A B C$ 满足条件时，四边形 $A D C E$ 是矩形．

查看试题解析
24. 如图，小军、小丽、小华利用晚间放学时间完成一个综合实践活动，活动内容是测量人行路上的路灯高度．小军和小丽分别站在路灯的两侧，小军站在水平地面上的点 $A$ 处，小丽站在点 $C$ 处，这时小军的身高 $A B$ 形成的影子为 $A E$ ，小丽身高 $C D$ 形成的影子为 $C F$ ．

(1)、请画图确定灯泡 $P$ 的位置

(2)、已知小军和小丽的身高分别为1.8米和1.6米，小华测得小军和小丽在路灯下的影子 $A E$ 和 $C F$ 分别为1米和2米，小军和小丽之间的距离 $A C$ 为10米，点 $E$ ， $A$ ， $C$ ， $F$ 在同一条直线上，请帮助他们3人求出路灯的高度．

查看试题解析
25. 如图，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象与一次函数 $y = m x - 2$ 相交于 $A (6 ， 1)$ ， $B (n ， - 3)$ ，直线 $A B$ 与 $x$ 轴， $y$ 轴分别交于点 $C$ ， $D$ ．

(1)、求 $k$ ， $m$ 的值；

(2)、求出 $B$ 点坐标，再直接写出不等式 $m x - 2 < \frac{k}{x}$ 的解集；

(3)、点 $M$ 在函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上，点 $N$ 在 $x$ 轴上，若以 $C$ 、 $D$ 、 $M$ 、 $N$ 为顶点的四边形是平行四边形，请你直接写出 $N$ 点坐标．

查看试题解析
26. 如图1，点 $O$ 为正方形 $A B C D$ 对角线 $A C$ 的中点， $O A = 3 \sqrt{2}$ ，点 $M$ 为边 $A D$ 上一动点，连接 $O M$ ，过点 $O$ 作 $NF ⊥ OM$ ，分别交 $D C$ ， $A B$ 于点 $N$ ， $F$ ．过点 $D$ 作 $D E ⊥ O M$ 于点 $H$ ，交直线 $A B$ 于点 $E$ ．

(1)、①如图2，当点 $M$ 与点 $A$ 重合时，可知点 $D$ ， $N$ 重合，点 $E$ ， $F$ ， $B$ 重合，请直接写出此时 $D M$ 与 $O A$ 之间的数量关系是；
②请你猜想图1中线段 $D M$ ， $E F$ 与 $O A$ 之间的数量关系是；并证明你的猜想．

(2)、点 $M$ 在 $A D$ 上运动的过程中，当 $A E = 1.5$ 时，请直接写出 $D H$ 的长度．

查看试题解析