陕西省延安市富县2021-2022学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-11-09 类型:月考试卷
一、单选题
-
1. 下列方程中,是关于x的一元二次方程的是( )A、 B、 C、 D、2. 若 是关于x的一元二次方程 的一个根,则m的值为( )A、 B、 C、 D、3. 抛物线 的顶点坐标为( )A、 B、 C、 D、4. 用配方法解 方程,将其化成 的形式,则变形正确的是( )A、 B、 C、 D、5. 已知关于x的一元二次方程 ,其中m , n在数轴上的对应点如图所示,则这个方程的根的情况是( )
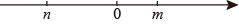 A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定6. 在同一平面直角坐标系中,二次函数 与一次函数 的图象如图所示,则二次函数 的图象可能是( )
A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定6. 在同一平面直角坐标系中,二次函数 与一次函数 的图象如图所示,则二次函数 的图象可能是( )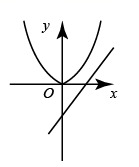 A、
A、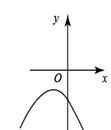 B、
B、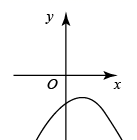 C、
C、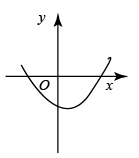 D、
D、 7. 要组织一次篮球联赛,赛制为单循环形式.每两队之间都赛一场,计划安排21场比赛.设比赛组织者应邀请x个队参赛,则x满足的关系式为( )A、 B、 C、 D、8. 如图是二次函数 的图象,以下结论:① ;② ;③ 的两个根是 , ;④ ,其中正确的是( )
7. 要组织一次篮球联赛,赛制为单循环形式.每两队之间都赛一场,计划安排21场比赛.设比赛组织者应邀请x个队参赛,则x满足的关系式为( )A、 B、 C、 D、8. 如图是二次函数 的图象,以下结论:① ;② ;③ 的两个根是 , ;④ ,其中正确的是( )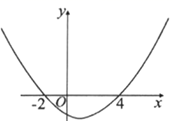 A、①③④ B、①② C、②③④ D、①②③④
A、①③④ B、①② C、②③④ D、①②③④二、填空题
-
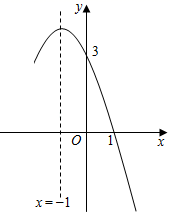
9. 方程 的根是.10. 下列表格是二次函数 中x,y的部分对应值,则一元二次方程 的一个近似解是.(精确度0.1)11. 关于x的一元二次方程 有两个实数根,则a的取值范围是.12. 抛物线y=﹣x2+bx+c的部分图象如图所示,其对称轴是x=﹣1,若y≥3,则x的取值范围为 .
 13. 已知抛物线 的对称轴在y轴右侧,现将该抛物线先向右平移3个单位长度,再向上平移1个单位长度后,得到的抛物线正好经过坐标原点,则b的值是.
13. 已知抛物线 的对称轴在y轴右侧,现将该抛物线先向右平移3个单位长度,再向上平移1个单位长度后,得到的抛物线正好经过坐标原点,则b的值是.三、解答题
-
14. 用配方法解方程: .15. “杂交水稻之父”—袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量 公斤的目标,第三阶段实现水稻亩产量 公斤的目标.如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率.16. 若点 , , 在抛物线 的图象上,请判断 , , 的大小关系,并说明理由.17. 一个等腰三角形的两条边长分别是方程 的两根,求该等腰三角形的周长.18. 若抛物线 的图象经过四个象限,求k的取值范围.19. 2021年7日1日建党100周年纪念日,在本月日历表上可以用一个方框圈出4个数(如图所示),若圈出的四个数中,最小数与最大数的乘积为65,求这个最小数(请用方程知识解答).
 20. 阅读下列解方程x2﹣9=2(x﹣3)的过程,并解决相关问题.
20. 阅读下列解方程x2﹣9=2(x﹣3)的过程,并解决相关问题.解:将方程左边分解因式,得(x+3)(x﹣3)=2(x﹣3),…第一步
方程两边都除以(x﹣3),得x+3=2,…第二步
解得x=﹣1…第三步
①第一步方程左边分解因式的方法是 , 解方程的过程从第步开始出现错误,错误的原因是;
②请直接写出方程的根为.
21. 如图,李叔叔从市场上买回一块矩形铁皮,他将此铁皮的四个角各剪去一个边长为 的正方形后,剩下的部分刚好能围成一个容积为 的无盖长方体箱子,且此长方体箱子的底面长比宽多 .现已知购买这种铁皮每平方米需 元钱,问李叔叔购回这矩形铁皮共花费多少元? 22. 已知关于x的一元二次方程x2﹣(m﹣2)x+2m﹣8=0.(1)、求证:方程总有两个实数根.(2)、若方程有一个根是负数,求m的取值范围.23. 已知二次函数图象的顶点是 ,且过点 .(1)、求二次函数的表达式;(2)、判断该二次函数的图象是否经过点 ,并解释你的判断.24. 某班“数学兴趣小组”对函数 的图象和性质进行了探究,探究过程如下,请补充完整.
22. 已知关于x的一元二次方程x2﹣(m﹣2)x+2m﹣8=0.(1)、求证:方程总有两个实数根.(2)、若方程有一个根是负数,求m的取值范围.23. 已知二次函数图象的顶点是 ,且过点 .(1)、求二次函数的表达式;(2)、判断该二次函数的图象是否经过点 ,并解释你的判断.24. 某班“数学兴趣小组”对函数 的图象和性质进行了探究,探究过程如下,请补充完整.
0
1
2
3
3
0
0
0
3
(1)、根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分;(2)、观察函数图象,写出2条函数的性质;(3)、进一步探究函数图象发现:①方程 的实数根为;
②方程 有个实数根.
③关于x的方程 有4个实数根时,a的取值范围.
25. 直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.(1)、若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?(2)、小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?26. 如图,已知抛物线 与x轴交于 、B两点,与y轴交于C点,其对称轴为直线 . (1)、直接写出抛物线的解析式;(2)、把线段 沿x轴向右平移,设平移后A、C的对应点分别为 、 ,当 落在抛物线上时,求 、 的坐标;(3)、除(2)中的平行四边形 外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形?若存在,求出E、F的坐标;若不存在,请说明理由.
(1)、直接写出抛物线的解析式;(2)、把线段 沿x轴向右平移,设平移后A、C的对应点分别为 、 ,当 落在抛物线上时,求 、 的坐标;(3)、除(2)中的平行四边形 外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形?若存在,求出E、F的坐标;若不存在,请说明理由.