辽宁省大连市中山区2020-2021学年九年级第一学期期末数学试卷
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件中,是必然事件的是( )A、通常加热到100℃时,水沸腾 B、篮球队员在罚球线上投篮一次,未投中 C、射击运动员射击一次,命中靶心 D、掷一次骰子,向上一面的点数为63. 要得到抛物线 ,可以将抛物线 ( )A、向左平移6个单位,再向上平移3个单位 B、向左平移6个单位,再向下平移3个单位 C、向右平移6个单位,再向上平移3个单位 D、向右平移6个单位,再向下平移3个单位4. 已知 ,其相似比为3:2,则 与 的周长之比为( )A、2:3 B、3:2 C、4:9 D、9:45. 在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为( )A、 B、 C、 D、6. 如图,A,B,C是 上的三点, ,则 的度数为( )
2. 下列事件中,是必然事件的是( )A、通常加热到100℃时,水沸腾 B、篮球队员在罚球线上投篮一次,未投中 C、射击运动员射击一次,命中靶心 D、掷一次骰子,向上一面的点数为63. 要得到抛物线 ,可以将抛物线 ( )A、向左平移6个单位,再向上平移3个单位 B、向左平移6个单位,再向下平移3个单位 C、向右平移6个单位,再向上平移3个单位 D、向右平移6个单位,再向下平移3个单位4. 已知 ,其相似比为3:2,则 与 的周长之比为( )A、2:3 B、3:2 C、4:9 D、9:45. 在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为( )A、 B、 C、 D、6. 如图,A,B,C是 上的三点, ,则 的度数为( ) A、100° B、110° C、125° D、130°7. 如图,直线 ,直线AC和DF被 , , 所截, , , ,则DE的长为( )
A、100° B、110° C、125° D、130°7. 如图,直线 ,直线AC和DF被 , , 所截, , , ,则DE的长为( ) A、2 B、3 C、 D、8. 如图,线段CD两个端点的坐标分别为C(6,6)、D(8,2),以原点O为位似中心,在第一象限内将线段CD缩小为原来的 后得到线段AB,则端点B的坐标为( )
A、2 B、3 C、 D、8. 如图,线段CD两个端点的坐标分别为C(6,6)、D(8,2),以原点O为位似中心,在第一象限内将线段CD缩小为原来的 后得到线段AB,则端点B的坐标为( ) A、(3,3) B、(4,3) C、(3,1) D、(4,1)9. 正六边形的边心距是 ,则正六边形的边长是( )A、 B、1 C、2 D、10. 在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一栋楼的影长为90m,则这栋楼的高度是( )A、36m B、54m C、96m D、150m
A、(3,3) B、(4,3) C、(3,1) D、(4,1)9. 正六边形的边心距是 ,则正六边形的边长是( )A、 B、1 C、2 D、10. 在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一栋楼的影长为90m,则这栋楼的高度是( )A、36m B、54m C、96m D、150m二、填空题
-
11. 柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:
种子数n
30
75
130
210
480
856
1250
2300
发芽数m
28
72
125
200
457
814
1187
2185
发芽频率
0.9333
0.9600
0.9615
0.9524
0.9521
0.9509
0.9496
0.9500
依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是(结果精确到0.01).
12. 如图, 中, , ,则 的度数为 . 13. 如图是抛物线y=ax2+bx+c的图象的一部分,请你根据图象写出方程ax2+bx+c=0的两根是 .
13. 如图是抛物线y=ax2+bx+c的图象的一部分,请你根据图象写出方程ax2+bx+c=0的两根是 . 14. 75°的圆心角所对的弧长是 cm,则此弧所在圆的半径是cm.15. 二次函数y=ax2+bx+c(0≤x≤3)的图象如图所示,则y的取值范围是 .
14. 75°的圆心角所对的弧长是 cm,则此弧所在圆的半径是cm.15. 二次函数y=ax2+bx+c(0≤x≤3)的图象如图所示,则y的取值范围是 . 16. 如图,矩形ABCD中, ,将矩形ABCD绕点D顺时针旋转90°,点A、C分别落在点 、 处,如果点 、 、 在同一条直线上,则AB的长为 .
16. 如图,矩形ABCD中, ,将矩形ABCD绕点D顺时针旋转90°,点A、C分别落在点 、 处,如果点 、 、 在同一条直线上,则AB的长为 .
三、解答题
-
17. 如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,求AD的长
 18. 如图所示,已知 的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).(1)、请直接写出点A关于点O对称的点的坐标;(2)、将 绕坐标原点O逆时针旋转90°,得到 ,画出图形,并直接写出点 、 、 的坐标.
18. 如图所示,已知 的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).(1)、请直接写出点A关于点O对称的点的坐标;(2)、将 绕坐标原点O逆时针旋转90°,得到 ,画出图形,并直接写出点 、 、 的坐标.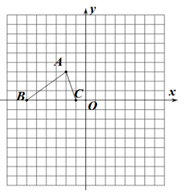 19. 如图,AB是 的弦,CD是 的直径, ,垂足为E.如果 , ,求AB长.
19. 如图,AB是 的弦,CD是 的直径, ,垂足为E.如果 , ,求AB长. 20. 为了做好防控H1N1甲型流感工作,我县卫生局准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士指导某乡镇预防H1N1甲型流感工作.(1)、若随机选一位医生和一名护士,用树状图(或列表法)表示所有可能出现的结果.(2)、求恰好选中医生甲和护士A的概率.21. 某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如果调整价格每件的售价每涨1元,那么每星期少卖10件.已知商品的进价为每件40元.设每件涨价x元,每星期的销量为y件.(1)、写出y与x的函数解析式及自变量x的取值范围;(2)、如何定价才能使每星期的利润最大?每星期的最大利润是多少?22. 在 中,弦CD与直径AB相交于点P, .
20. 为了做好防控H1N1甲型流感工作,我县卫生局准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士指导某乡镇预防H1N1甲型流感工作.(1)、若随机选一位医生和一名护士,用树状图(或列表法)表示所有可能出现的结果.(2)、求恰好选中医生甲和护士A的概率.21. 某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如果调整价格每件的售价每涨1元,那么每星期少卖10件.已知商品的进价为每件40元.设每件涨价x元,每星期的销量为y件.(1)、写出y与x的函数解析式及自变量x的取值范围;(2)、如何定价才能使每星期的利润最大?每星期的最大利润是多少?22. 在 中,弦CD与直径AB相交于点P, . (1)、如图1,若 ,求 和 的大小;(2)、如图2,若 ,过点D作 的切线,与AB的延长线相交于点E,求 的大小.23. 如图,直线 与x轴于交于点B,与y轴交于点C.抛物线 经过B、C两点,并与x轴另一个交点为A.
(1)、如图1,若 ,求 和 的大小;(2)、如图2,若 ,过点D作 的切线,与AB的延长线相交于点E,求 的大小.23. 如图,直线 与x轴于交于点B,与y轴交于点C.抛物线 经过B、C两点,并与x轴另一个交点为A. (1)、求抛物线 的解析式;(2)、若点M在抛物线上,且 ,求点M的坐标;(3)、设点P是线段BC上一动点,过P作 轴,交抛物线于点Q,求线段PQ长度的最大值.24. 在 中, , , ,动点D从点A出发沿线段AB以每秒1个单位长的速度运动至点B,过点D作 交射线AC于点E,设点D的运动时间为t秒( ),
(1)、求抛物线 的解析式;(2)、若点M在抛物线上,且 ,求点M的坐标;(3)、设点P是线段BC上一动点,过P作 轴,交抛物线于点Q,求线段PQ长度的最大值.24. 在 中, , , ,动点D从点A出发沿线段AB以每秒1个单位长的速度运动至点B,过点D作 交射线AC于点E,设点D的运动时间为t秒( ), (1)、线段CE的长为(用含t的代数式表示);(2)、设 与 重叠部分图形的面积为S,求S与t之间的函数关系式.
(1)、线段CE的长为(用含t的代数式表示);(2)、设 与 重叠部分图形的面积为S,求S与t之间的函数关系式.
