辽宁省大连市沙河口区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
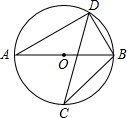
1. 下列事件中,属于必然事件的是( )A、通常加热到100℃时,水沸腾 B、某射击运动员射击一次,命中靶心 C、任意画一个三角形,其内角和是360° D、抛一枚硬币,落地后正面朝上2. 把抛物线 向左平移1个单位,再向下平移2个单位,所得抛物线的解析式为( )A、 B、 C、 D、3. 在平面直角坐标系中,点 关于原点对称的点的坐标是( )A、 B、 C、 D、4. 如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=50°,则∠C的度数为( )
 A、60° B、50° C、40° D、30°5. 掷一枚质地均匀的骰子,观察向上一面的点数,则点数为2的概率为( )A、 B、 C、 D、6. 如图,在 中,若 , , ,则 的长是( )
A、60° B、50° C、40° D、30°5. 掷一枚质地均匀的骰子,观察向上一面的点数,则点数为2的概率为( )A、 B、 C、 D、6. 如图,在 中,若 , , ,则 的长是( )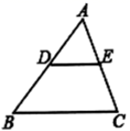 A、 B、 C、 D、7. 已知圆锥的母线长为12,底面圆半径为6,则圆锥的侧面积是( )A、24π B、36π C、70π D、72π8. 关于二次函数 图象,下列叙述正确的有( )
A、 B、 C、 D、7. 已知圆锥的母线长为12,底面圆半径为6,则圆锥的侧面积是( )A、24π B、36π C、70π D、72π8. 关于二次函数 图象,下列叙述正确的有( )①它的图象是抛物线; ②它的图象有最低点;
③它的图象经过 ; ④它的图象开口向上.
A、4个 B、3个 C、2个 D、1个9. 如图,将直角三角形ABC(∠BAC=90°)绕点A逆时针旋转一定角度得到直角三角形ADE,若∠CAE=65°,∠AFB=90°,则∠D的度数为( ) A、60° B、35° C、25° D、15°10. Rt△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,r为半径作⊙C,则正确的是( )A、当r=2时,直线AB与⊙C相交 B、当r=3时,直线AB与⊙C相离 C、当r=2.4时,直线AB与⊙C相切 D、当r=4时,直线AB与⊙C相切
A、60° B、35° C、25° D、15°10. Rt△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,r为半径作⊙C,则正确的是( )A、当r=2时,直线AB与⊙C相交 B、当r=3时,直线AB与⊙C相离 C、当r=2.4时,直线AB与⊙C相切 D、当r=4时,直线AB与⊙C相切二、填空题
-
11. 函数 的顶点坐标为 .12. 等边三角形绕着它的中心旋转,旋转后的等边三角形能和自身重合,则旋转角至少为 .13. 在 中,弦 的长为8cm,圆心 到 的距离为3cm,则 的半径为cm.14. 从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数
100
400
800
1000
2000
5000
发芽种子粒数
85
298
652
793
1604
4005
发芽频率
0.850
0.745
0.815
0.793
0.802
0.801
根据以上数据可以估计,该玉米种子发芽的概率约为(精确到0.1).
15. 如图,在 中, , ,正方形 的顶点 、 分别在 、 上,顶点 , 在 内, , ,则点 到 的距离为 . 16. 已知关于 的函数 图象与坐标轴只有2个交点,则 .
16. 已知关于 的函数 图象与坐标轴只有2个交点,则 .三、解答题
-
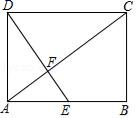
17. 计算: .18. 二次函数 的图象与 轴交于点 和点 .(1)、求这个二次函数的解析式;(2)、判断 是否在此函数图象上,并说明理由.19. 如图,在矩形ABCD中,E是边AB的中点,连接DE交对角线AC于点F,
(Ⅰ)求证:△AFE∽△CFD;
(Ⅱ)若AB=4,AD=3,求CF的长.
 20. 为了迎接文艺汇演,甲班选出了2名女生候选人,乙班选出了一男一女两名候选人,要从这4名同学中选出2名同学担任文艺汇演的主持人,求下列事件的概率:(1)、求所选的2名主持人性别相同的概率;(2)、求所选的2名同学来自同一个班级的概率.21. 某商店进了一批成本为每件40元的商品,经调查,销售量 (件)与销售单价 (元)的函数关系为 .销售单价定位多少元,才能使销售该商品每天获得的利润 (元)最大?最大利润是多少?22. 为了测量一条两岸平行的河流宽度,数学研究小组设计了如下的方案,他们在河南岸的点 处测得河北岸的树 恰好在 的正北方向,点 在点 的正东方向,点 在点 的正西方向,测量得到:数据 , , .请根据测量数据求出河宽(结果保留根号).
20. 为了迎接文艺汇演,甲班选出了2名女生候选人,乙班选出了一男一女两名候选人,要从这4名同学中选出2名同学担任文艺汇演的主持人,求下列事件的概率:(1)、求所选的2名主持人性别相同的概率;(2)、求所选的2名同学来自同一个班级的概率.21. 某商店进了一批成本为每件40元的商品,经调查,销售量 (件)与销售单价 (元)的函数关系为 .销售单价定位多少元,才能使销售该商品每天获得的利润 (元)最大?最大利润是多少?22. 为了测量一条两岸平行的河流宽度,数学研究小组设计了如下的方案,他们在河南岸的点 处测得河北岸的树 恰好在 的正北方向,点 在点 的正东方向,点 在点 的正西方向,测量得到:数据 , , .请根据测量数据求出河宽(结果保留根号).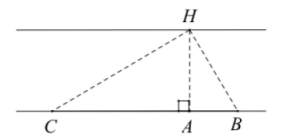 23. 如图,在 中, 为直径,点 为 上一点,点 是 延长线上一点,过点 作 的垂线交 的延长线于点 ,且 .
23. 如图,在 中, 为直径,点 为 上一点,点 是 延长线上一点,过点 作 的垂线交 的延长线于点 ,且 .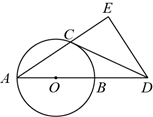 (1)、求证 为 的切线;(2)、若 , ,求 的半径.24. 如图,已知 是边长为6的等边三角形, 为 上的一点, ,动点 为边 一点,动点 从 点出发,当点 到达点 时,整个运动停止,连接 ,作 , 交射线 于点 .设 ,以点 、 、 、 为顶点的四边形的面积为 .
(1)、求证 为 的切线;(2)、若 , ,求 的半径.24. 如图,已知 是边长为6的等边三角形, 为 上的一点, ,动点 为边 一点,动点 从 点出发,当点 到达点 时,整个运动停止,连接 ,作 , 交射线 于点 .设 ,以点 、 、 、 为顶点的四边形的面积为 . (1)、 (用含 的代数式表示)(2)、试求 关于 的函数解析式,并写出自变量的取值范围.
(1)、 (用含 的代数式表示)(2)、试求 关于 的函数解析式,并写出自变量的取值范围.