辽宁省大连市高新区2020-2021学年九年级上学期期末测试数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 反比例函数y=﹣ $\frac{2}{x}$ 的图象在（　　）

A、第二、四象限 B、第一、三象限 C、第一、二象限 D、第三、四象限

查看试题解析
3. 一元二次方程 $x (x - 2) = x - 2$ 的根是（）

A、 $x = 2$ B、 $x_{1} = 0, x_{2} = 2$ C、 $x_{1} = 2, x_{2} = 1$ D、 $x = - 1$

查看试题解析
4. 在 $△ A B C$ 中， $∠ C = 90 °$ ， $A B = 6$ ， $cos A = \frac{1}{3}$ ，则 $A C$ 等于（）

A、3 B、2 C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

查看试题解析
5. 将抛物线 $y = - 2 x^{2}$ 先向左平移1个单位长度，再向下平移3个单位长度，得到的抛物线的解析式是（）

A、 $y = - 2 {(x - 1)}^{2} - 3$ B、 $y = - 2 {(x - 1)}^{2} + 3$ C、 $y = - 2 {(x + 1)}^{2} - 3$ D、 $y = - 2 {(x + 1)}^{2} + 3$

查看试题解析
6. 如图，AB∥CD，AB＝6，CD＝9，AD＝10，则OD的长为（）

A、4 B、5 C、6 D、7

查看试题解析
7. 某校有两块运动场地，甲、乙、丙三名学生各自随机选择其中的某个运动场地进行跑步训练，则甲、乙、丙三名学生在同一块场地跑步训练的概率为（）

A、 $\frac{3}{4}$ B、 $\frac{2}{3}$ C、 $\frac{3}{8}$ D、 $\frac{1}{4}$

查看试题解析
8. 如图，BC是⊙O的直径，A是⊙O上的一点，∠OAC=32°，则∠B的度数是（）

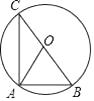A、58° B、60° C、64° D、68°

查看试题解析
9. 抛物线 $y = - x^{2} + b x + c$ 与 $x$ 轴的一个交点坐标为 $(1 ， 0)$ ，对称轴是直线 $x = - 1$ ，其部分图象如图所示，若 $y > 0$ ，则 $x$ 的取值范围是（）

A、 $- 4 < x < 1$ B、 $- 3 < x < 1$ C、 $- 2 < x < 1$ D、 $x < 1$

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，将 $△ A B C$ 绕点 $A$ 顺时针旋转 $90 °$ ，得到 $△ A D E$ ，连接 $B D$ ，若 $A C = 2 \sqrt{2}$ ， $D E = 1$ ，则线段 $B D$ 的长为（）

A、3 B、 $3 \sqrt{2}$ C、 $2 \sqrt{7}$ D、 $2 \sqrt{10}$

查看试题解析

二、填空题

11. 在平面直角坐标系中，点（2，﹣1）关于原点对称的点的坐标是．

查看试题解析
12. 在一个不透明的袋子中有2个白球、3个红球，这些球除颜色不同外其他完全相同．从袋子中随机摸出一个球，它是红球的概率是．

查看试题解析
13. 已知圆锥的底面半径为 $2 c m$ ，母线长为 $5 c m$ ，则圆锥的侧面积是.

查看试题解析
14. 在全国人民的共同努力下．新冠肺炎得到有效控制，据统计，某地区2月份新冠肺炎确诊病例121例，4月份新冠肺炎确诊病例25例，设这两个月确诊病例平均每月降低的百分率是 $x$ ，根据题意可列方程为．

查看试题解析
15. 如图，在平面直角坐标系中，一次函数 $y = x + 1$ 的图象与 $x$ 轴、 $y$ 轴的交点分别为点 $A$ 、点 $B$ ，与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象交于点 $C$ ， $C E ⊥ x$ 轴于点 $E$ ， $A C = 2 \sqrt{2}$ ，则 $k$ 的值为．

查看试题解析
16. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $A B = 5$ ， $A C = 3$ ，点 $D$ 在 $B C$ 边上，点 $E$ 在 $A B$ 边上， $∠ A D E = ∠ B$ ，设 $B D$ 的长为 $x$ ， $A E$ 的长为 $y$ ， $y$ 关于 $x$ 的函数解析式为．

查看试题解析

三、解答题

17. 已知关于 $x$ 的一元二次方程 $x^{2} - 8 x + c = 0$ 有两个相等的实数根，求 $c$ 的值及方程的根．

查看试题解析
18. 二次函数 $y = a x^{2} + b x + c$ 图象与 $x$ 轴交于点 $A (- 1 ， 0)$ ，与 $y$ 轴交于点 $C (0 ， - 5)$ ，且经过点D（3，-8）．求此二次函数的解析式及顶点坐标．

查看试题解析
19. 如图， $A E$ 是 $△ A B C$ 的角平分线，延长 $A E$ 至 $D$ ，连结 $C D$ ，使 $A C = C D$ ．

(1)、求证： $△ A B E ∽ △ D C E$ ；

(2)、若 $A C = 2 A B$ ， $B C = 3$ ，求 $B E$ 的长．

查看试题解析
20. 如图，一艘渔船在 $A$ 处测得小岛 $C$ 位于它的北偏东 $54 °$ 方向，再向东航行一段距离到达 $B$ 处，测得小岛 $C$ 位于它的北偏东 $30 °$ 方向，且与渔船相距30海里．求渔船从 $A$ 到 $B$ 航行了多少海里？
（结果保留整数．参考数据： $sin 54 ° \approx 0.81$ ， $cos 54 ° \approx 0.59$ ， $tan 54 ° \approx 1.38$ ， $\sqrt{3} \approx 1.73$ ．）

查看试题解析
21. 如图，某农场有一块长 $20 m$ ，宽 $16 m$ 的矩形种植地，为方便管理，准备沿平行于两边的方向纵、横各修建一条等宽的小路，要使种植面积为 $252 m^{2}$ ，求小路的宽．

查看试题解析
22. 如图等腰 $△ A B C$ ， $A B = A C$ ， $O$ 为 $A C$ 上一点， $⊙ O$ 经过点 $C$ 且与 $A B$ 相切于 $E$ 点， $⊙ O$ 与 $B C$ 交于点 $D$ ，作 $D F ⊥ A B$ ，垂足为 $F$ ．

(1)、求证： $D F$ 为 $⊙ O$ 的切线；

(2)、若 $A E = 3$ ， $D F = 4$ ，求 $A C$ 的长．

查看试题解析
23. 某商场经销一种商品，每件进价为40元．市场调查发现，该商品每星期的销售量 $y$ （件）与销售单价 $x$ （元）之间的函数关系如图中线段 $A B$ 所示．

(1)、求出该商品每星期的销售量 $y$ （件）与销售单价 $x$ （元）之间的函数关系式，并写出自变量 $x$ 的取值范围；

(2)、当该商品每件的销售价定为多少元时，商场每星期经销该商品能够获得最大销售利润？最大销售利润是多少？

查看试题解析
24. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $A C = 2 B C$ ， $A B = 4 \sqrt{7}$ cm，点 $D$ 从点 $A$ 出发，沿 $A B$ 以2cm/s的速度向终点 $B$ 运动，当点 $D$ 与点 $A$ 、 $B$ 不重合时，过点 $D$ 作 $D E ⊥ A B$ 交射线 $A C$ 于点 $E$ ，以 $A D$ 、 $A E$ 为邻边向上作平行四边形 $A D F E$ ，设 $D$ 点的运动时间为 $t (s)$ ，平行四边形 $A D F E$ 与 $△ A B C$ 的重叠部分图形的面积为 $s ({cm}^{2})$ ．

(1)、填空： $A C =$ $cm$ ， $B C =$ $cm$ ；

(2)、当点 $F$ 在 $B C$ 上时，求 $t$ 的值；

(3)、求 $s$ 与 $t$ 的函数解析式，并直接写出自变量 $t$ 的取值范围．

查看试题解析
25. 阅读下面材料，完成（1）-（3）题．
数学课上，老师出示了这样一道题：

如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ 于 $D$ ，点 $E$ 为线段 $B D$ 上一点，延长 $C E$ 至点 $F$ ，连结 $B F$ ，使 $∠ F = ∠ B C D$ ，且 $2 ∠ F + ∠ B C F = 90 °$ ，求证： $A C = F C$ ．

同学们经过思考后，交流了自己的想法：

小明：“通过观察和度量，发现 $∠ A$ 与 $∠ F$ 相等．”

小涛：“利用这学期学的图形的旋转，构造全等三角形，可以解决问题”．

……

老师：“保留原题条件，若 $C D = k B F$ ，则可求 $\frac{A D}{B F}$ 的值．”

(1)、求证： $∠ A = ∠ F$ ；

(2)、求让： $A C = F C$ ；

(3)、若 $C D = k B F$ ，求 $\frac{A D}{B F}$ 的值（用含 $k$ 的式子表示）．

查看试题解析
26. 在平面直角坐标系中，抛物线 $y = x^{2} - 2 x + n (x > 0)$ 的图象记为 $G_{1}$ ，将 $G_{1}$ 绕坐标原点 $O$ 旋转 $180 °$ 得到图象 $G_{2}$ ，图象 $G_{1}$ 和 $G_{2}$ 合起来记为图象 $G$ ．

(1)、若点 $E (- 2 ， 1)$ 在图象 $G$ 上，求 $n$ 的值；

(2)、若 $n = - 3$ ．
①若点 $F (t ， 1)$ 在图象 $G$ 上，求 $t$ 的值；

②当 $m \leq x \leq \frac{7}{2} (m < \frac{7}{2})$ 时，图象 $G$ 对应函数的最大值为4，最小值为 $- 4$ ，求 $m$ 的取值范围；

(3)、当以 $A (2 ， 2)$ 、 $B (- 2 ， 2)$ 、 $C (- 2 ， - 2)$ 、 $D (2 ， - 2)$ 为顶点的正方形 $A B C D$ 的边与图象 $G$ 有且只有两个公共点时，直接写出 $n$ 的值或取值范围．

查看试题解析