辽宁省鞍山市2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、等边三角形 B、平行四边形 C、正五边形 D、圆2. 一元二次方程4x2+1=4x的根的情况是( )A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根3. 把抛物线y=2x2先向左平移3个单位,再向上平移4个单位,所得抛物线的函数表达式为( )A、y=2(x+3)2+4 B、y=2(x+3)2﹣4 C、y=2(x﹣3)2﹣4 D、y=2(x﹣3)2+44. 如图, 是⊙ 的直径, , 是圆上两点, ,则 的度数为( )
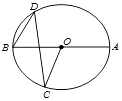 A、 B、 C、 D、5. 是 绕点 顺时针方向旋转 后所得的图形,点 恰好在 上,则 的度数为( )
A、 B、 C、 D、5. 是 绕点 顺时针方向旋转 后所得的图形,点 恰好在 上,则 的度数为( )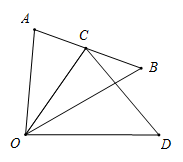 A、 B、 C、 D、6. 某超市1月份的营业额是0.2亿元,第一季度的营业额共1亿元.如果平均每月增长率为
A、 B、 C、 D、6. 某超市1月份的营业额是0.2亿元,第一季度的营业额共1亿元.如果平均每月增长率为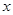 ,则由题意列方程应为( ) A、0.2(1+
,则由题意列方程应为( ) A、0.2(1+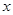 )2=1
B、0.2+0.2×2
)2=1
B、0.2+0.2×2 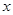 =1
C、0.2+0.2×3
=1
C、0.2+0.2×3 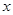 =1
D、0.2×[1+(1+
=1
D、0.2×[1+(1+ 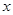 )+(1+
)+(1+ 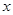 )2]=1
7. 如图,在平行四边形ABCD中,点E是AB的中点,CE和BD交于点O,若S△EOB=1,则四边形AEOD的面积为( )
)2]=1
7. 如图,在平行四边形ABCD中,点E是AB的中点,CE和BD交于点O,若S△EOB=1,则四边形AEOD的面积为( )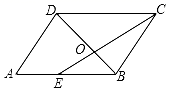 A、4 B、5 C、6 D、78. 如图,菱形ABCD的对角线AC与BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B→A→D在菱形ABCD的边AB,AD上运动,运动到点D停止.点P′是点P关于BD的对称点,连接PP'交BD于点M,若BM=x(0<x<8),△DPP′的面积为y,下列图象能正确反映y与x的函数关系的是( )
A、4 B、5 C、6 D、78. 如图,菱形ABCD的对角线AC与BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B→A→D在菱形ABCD的边AB,AD上运动,运动到点D停止.点P′是点P关于BD的对称点,连接PP'交BD于点M,若BM=x(0<x<8),△DPP′的面积为y,下列图象能正确反映y与x的函数关系的是( )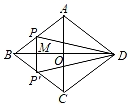 A、
A、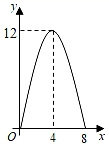 B、
B、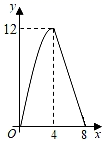 C、
C、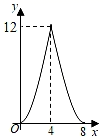 D、
D、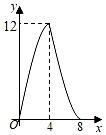
二、填空题
-
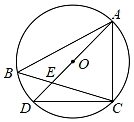
9. 中心角为30°的正多边形边数为 .10. 反比例函数的图象经过点P(﹣1,2),则此反比例函数的解析式为 .11. 已知△ABC∽△A'B'C',AD和A′D'是它们的对应中线,若AD=10,A'D'=8,则△ABC与△A'B'C′的周长比等于 .12. 已知x=1是一元二次方程x2﹣4x+k=0的一个根,则k= .13. 已知点A(4,y1),B( ,y2),C(﹣2,y3)都在二次函数y=(x﹣2)2+k的图象上,则y1、y2、y3的大小关系是 . (请用“>”连接)14. 如图,点A、B、C、D在⊙O上,AD是⊙O的直径,且AD=3 ,若∠ABC=∠CAD,BC交AD于点E,则CE•BC为 .
 15. 如图,在矩形ABCD中,BC=2AB,点E是边BC的中点,连接AE、DE,分别交BD、AC点P、Q,过点P作PF⊥AE交CB于点F,下列结论:①∠EAC=∠EDB;②AP=2PF;③若S△DQC= ,则AB=8;④CE•EF=EQ•DE.其中正确的结论有 . (填序号即可)
15. 如图,在矩形ABCD中,BC=2AB,点E是边BC的中点,连接AE、DE,分别交BD、AC点P、Q,过点P作PF⊥AE交CB于点F,下列结论:①∠EAC=∠EDB;②AP=2PF;③若S△DQC= ,则AB=8;④CE•EF=EQ•DE.其中正确的结论有 . (填序号即可)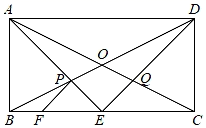 16. 如图,点A的坐标为(1,0),点B的坐标为(1,2),将 OAB绕点A第一次顺时针旋转90°得到 O1AB1 , 将 O1AB1绕点B1第二次顺时针旋转90°得到 O2A1B1 , 将 O2A1B1绕点B1第三次顺时针旋转90°得到 O3A2B1 , …,如此进行下去,则点O2021的坐标为 .
16. 如图,点A的坐标为(1,0),点B的坐标为(1,2),将 OAB绕点A第一次顺时针旋转90°得到 O1AB1 , 将 O1AB1绕点B1第二次顺时针旋转90°得到 O2A1B1 , 将 O2A1B1绕点B1第三次顺时针旋转90°得到 O3A2B1 , …,如此进行下去,则点O2021的坐标为 .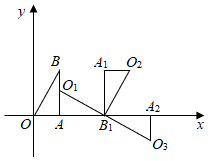
三、解答题
-
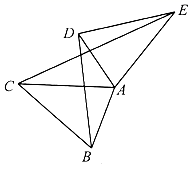
17. 用适当的方法解方程:(1)、 ;(2)、 .18. 如图,将△ABC绕点A旋转得到△ADE,连接BD,CE.求证:△ADB∽△AEC.
 19. 如图,一次函数y=kx+b的图象与反比例函数y= 的图象相交于A(-1,n),B(2,-1)两点,与y轴相交于点C.
19. 如图,一次函数y=kx+b的图象与反比例函数y= 的图象相交于A(-1,n),B(2,-1)两点,与y轴相交于点C.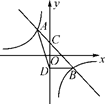 (1)、求一次函数与反比例函数的表达式;(2)、若点D与点C关于x轴对称,求△ABD的面积.20. 如图,要设计一个长为15cm,宽为10cm的矩形图案,其中有两横两竖彩条,横竖彩条的宽度之比为5:4,若使所有彩条所占面积是原来矩形图案面积的三分之一,应如何设计每个彩条的宽度?
(1)、求一次函数与反比例函数的表达式;(2)、若点D与点C关于x轴对称,求△ABD的面积.20. 如图,要设计一个长为15cm,宽为10cm的矩形图案,其中有两横两竖彩条,横竖彩条的宽度之比为5:4,若使所有彩条所占面积是原来矩形图案面积的三分之一,应如何设计每个彩条的宽度?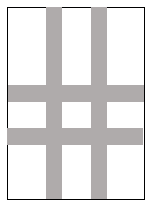 21. 小明根据学习函数的经验,对y=﹣1+ 的图象的性质进行了探究.
21. 小明根据学习函数的经验,对y=﹣1+ 的图象的性质进行了探究.下面是小明的探究过程,请补充完整;
(1)、函数y=﹣1+ 的自变量x取值范围为;(2)、完成表格,并画出函数的图象;x
…
-3
-2
-1
1
2
3
…
y
…
…
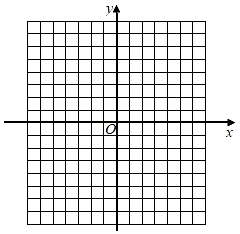 (3)、写出函数y=﹣1+ 的两条性质.22. 如图,在锐角△ABC中,点E是AB边上一点,BE=CE,AD⊥BC于点D,AD与EC交于点G.
(3)、写出函数y=﹣1+ 的两条性质.22. 如图,在锐角△ABC中,点E是AB边上一点,BE=CE,AD⊥BC于点D,AD与EC交于点G.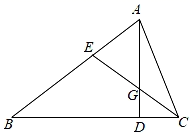 (1)、求证:∠BEC=2∠AGE;(2)、若 ,求 的值.23. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点,作△BCD的外接圆⊙O,CE是⊙O的直径,且CE与AB交于点G,DF∥EC交AC于点F.
(1)、求证:∠BEC=2∠AGE;(2)、若 ,求 的值.23. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点,作△BCD的外接圆⊙O,CE是⊙O的直径,且CE与AB交于点G,DF∥EC交AC于点F.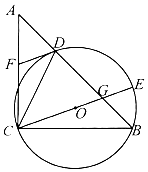 (1)、求证:DF为⊙O的切线;(2)、若 ,AC=5,求⊙O的半径长.24. 某服装厂自主经销一款精品服装,生产成本为500元/套,提价40%后进行销售,每周可以销售60件;受“新冠疫情”影响,原材料价格上涨,使得该款服装生产成本上涨,该服装厂决定在保持利润率不变的情况下提高销售价;调研发现该款服装生产成本上涨10元/套,每周销量就减少1套,若设该款服装生产成本上涨x元/套(x>0且x为10的整数倍),销售价为y元/套.(利润率= )(1)、求y与x之间函数关系式;(2)、设每周销售利润为w元,求w与x之间函数关系式,并求服装生产成本上涨多少元/套时,每周销售利润最大.25. 如图,在Rt△ACB中,∠ACB=90°,∠ABC=30°,点P、点G是射线BA上的两个动点,过G作AB的垂线,点E为该垂线上一点,连接CE,使得∠CEG=∠CPB.
(1)、求证:DF为⊙O的切线;(2)、若 ,AC=5,求⊙O的半径长.24. 某服装厂自主经销一款精品服装,生产成本为500元/套,提价40%后进行销售,每周可以销售60件;受“新冠疫情”影响,原材料价格上涨,使得该款服装生产成本上涨,该服装厂决定在保持利润率不变的情况下提高销售价;调研发现该款服装生产成本上涨10元/套,每周销量就减少1套,若设该款服装生产成本上涨x元/套(x>0且x为10的整数倍),销售价为y元/套.(利润率= )(1)、求y与x之间函数关系式;(2)、设每周销售利润为w元,求w与x之间函数关系式,并求服装生产成本上涨多少元/套时,每周销售利润最大.25. 如图,在Rt△ACB中,∠ACB=90°,∠ABC=30°,点P、点G是射线BA上的两个动点,过G作AB的垂线,点E为该垂线上一点,连接CE,使得∠CEG=∠CPB.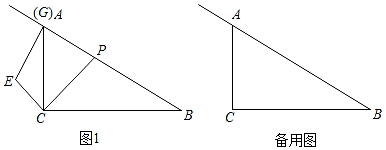 (1)、如图1,若点G与点A重合,
(1)、如图1,若点G与点A重合,①求 的值;
②当AE=AP=2时,求PC的长;
(2)、若点G与点A不重合,且AB=8AG,求 的值.26. 如图,抛物线y= x2+bx+c经过点B(﹣2,0)和点C(0,﹣2),与x轴交于点A.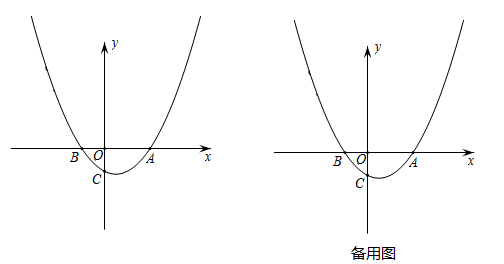 (1)、求抛物线的解析式;(2)、点P(0,n)是y轴上的一个动点,将线段OB绕点P顺时针旋转90°,得到线段O'B';
(1)、求抛物线的解析式;(2)、点P(0,n)是y轴上的一个动点,将线段OB绕点P顺时针旋转90°,得到线段O'B';①若线段O'B'与抛物线有一个公共点,结合函数图象,请直接写出n的取值范围;
②直线PB'交抛物线于M、N两点,若点B'是线段MN的中点,求n的值.