江西省上饶市余干县八校2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 如图是由一个长方体和一个球组成的几何体,它的主视图是( ).
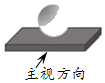 A、
A、 B、
B、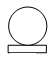 C、
C、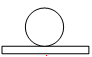 D、
D、 2. 点 在反比例函数 的图象上,则下列各点在此函数图象上的是( ).A、 B、 C、 D、3. 如图所示,P是等边三角形ABC内的一点,若将三角形PBC绕点B旋转到三角形P′BA,则∠P′BP的度数为( )
2. 点 在反比例函数 的图象上,则下列各点在此函数图象上的是( ).A、 B、 C、 D、3. 如图所示,P是等边三角形ABC内的一点,若将三角形PBC绕点B旋转到三角形P′BA,则∠P′BP的度数为( )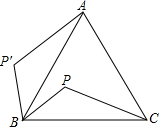 A、45° B、60° C、90° D、120°4. 关于 的一元二次方程 无实数根,则实数 的取值范围是( )A、 B、 C、 D、5. 如图,在⊙O中,∠BAC=15°,∠ADC=20°,则∠ABO的度数为( )
A、45° B、60° C、90° D、120°4. 关于 的一元二次方程 无实数根,则实数 的取值范围是( )A、 B、 C、 D、5. 如图,在⊙O中,∠BAC=15°,∠ADC=20°,则∠ABO的度数为( ) A、70° B、55° C、45° D、35°6. 小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时如下结论:①这个函数图象的顶点始终在直线y=-x+1上;②存在一个m的值,使得函数图象的顶点与 轴的两个交点构成等腰直角三角形;③点A(x1 , y1)与点B(x2 , y2)在函数图象上,若x1<x2 , x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2其中错误结论的序号是( )A、① B、② C、③ D、④
A、70° B、55° C、45° D、35°6. 小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时如下结论:①这个函数图象的顶点始终在直线y=-x+1上;②存在一个m的值,使得函数图象的顶点与 轴的两个交点构成等腰直角三角形;③点A(x1 , y1)与点B(x2 , y2)在函数图象上,若x1<x2 , x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2其中错误结论的序号是( )A、① B、② C、③ D、④二、填空题
-
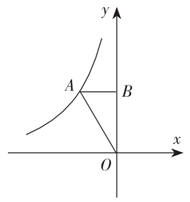
7. 一个布袋里装有2个红球、3个黄球和5个白球,除颜色外其它都相同,搅匀后任意摸出一个球,是白球的概率为 .8. 在 中,若 ,则 的度数是 .9. 如图,已知A为反比例函数 的图象上一点,过点A作 轴,垂足为B.若 的面积为2,则k的值为 .
 10. 如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,则弧 所对的圆周角∠FPG的大小为度.
10. 如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,则弧 所对的圆周角∠FPG的大小为度.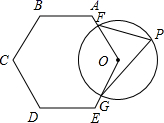 11. 在同车道行驶的机动车,后车应当与前车保持一定的安全距离.如图,在一个路口,一辆长为10m的大巴车遇红灯后停在距交通信号灯20m处,小林驾驶一辆小轿车,距大车尾xm,若大巴车车顶高于小林的水平视线0.8m,红灯下沿高于小林的水平视线3.2m,若小林能看到整个红灯,则x的最小值为.
11. 在同车道行驶的机动车,后车应当与前车保持一定的安全距离.如图,在一个路口,一辆长为10m的大巴车遇红灯后停在距交通信号灯20m处,小林驾驶一辆小轿车,距大车尾xm,若大巴车车顶高于小林的水平视线0.8m,红灯下沿高于小林的水平视线3.2m,若小林能看到整个红灯,则x的最小值为.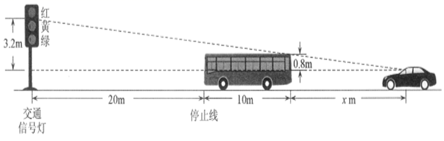 12. 如图,矩形ABCD中,AB=6,AD=4 ,点E是BC的中点,点F在AB上,FB=2,P是矩形上一动点.若点P从点F出发,沿F→A→D→C的路线运动,当∠FPE=30°时,FP的长为 .
12. 如图,矩形ABCD中,AB=6,AD=4 ,点E是BC的中点,点F在AB上,FB=2,P是矩形上一动点.若点P从点F出发,沿F→A→D→C的路线运动,当∠FPE=30°时,FP的长为 .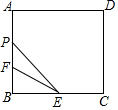
三、解答题
-
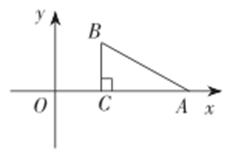
13.(1)、计算: .(2)、如图,在平面直角坐标系中, 的直角顶点C的坐标为 ,点A在x轴正半轴上,且 .将 先绕点C逆时针旋转90°,再向左平移3个单位,求变换后点A的对应点的坐标.
 14. 关于x的方程 有实数根,且m为正整数,求m的值及此时方程的根.15. 为落实立德树人的根本任务,加强思改、历史学科教师的专业化队伍建设.某校计划从前来应聘的思政专业(一名研究生,一名本科生)、历史专业(一名研究生、一名本科生)的高校毕业生中选聘教师,在政治思想审核合格的条件下,假设每位毕业生被录用的机会相等(1)、若从中只录用一人,恰好选到思政专业毕业生的概率是:(2)、若从中录用两人,请用列表或画树状图的方法,求恰好选到的是一名思政研究生和一名历史本科生的概率.16. 已知点 在⊙ 上, ,仅使用无刻度的直尺作图(保留痕迹)
14. 关于x的方程 有实数根,且m为正整数,求m的值及此时方程的根.15. 为落实立德树人的根本任务,加强思改、历史学科教师的专业化队伍建设.某校计划从前来应聘的思政专业(一名研究生,一名本科生)、历史专业(一名研究生、一名本科生)的高校毕业生中选聘教师,在政治思想审核合格的条件下,假设每位毕业生被录用的机会相等(1)、若从中只录用一人,恰好选到思政专业毕业生的概率是:(2)、若从中录用两人,请用列表或画树状图的方法,求恰好选到的是一名思政研究生和一名历史本科生的概率.16. 已知点 在⊙ 上, ,仅使用无刻度的直尺作图(保留痕迹)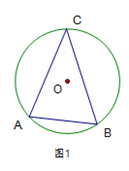
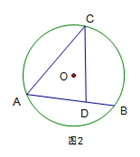 (1)、在图①中画一个含 的直角三角形;(2)、点 在弦 上,在图②中画一个含 的直角三角形.17. 为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2013年市政府共投资3亿元人民币建设了廉租房12万平方米,2015年投资6.75亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.(1)、求每年市政府投资的增长率;(2)、若这两年内的建设成本不变,问2015年建设了多少万平方米廉租房?18. 如图,直线y=x与反比例函数y= (x>0)的图象相交于点D,点A为直线y=x上一点,过点A作AC⊥x轴于点C,交反比例函数y= (x>0)的图象于点B,连接BD.
(1)、在图①中画一个含 的直角三角形;(2)、点 在弦 上,在图②中画一个含 的直角三角形.17. 为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2013年市政府共投资3亿元人民币建设了廉租房12万平方米,2015年投资6.75亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.(1)、求每年市政府投资的增长率;(2)、若这两年内的建设成本不变,问2015年建设了多少万平方米廉租房?18. 如图,直线y=x与反比例函数y= (x>0)的图象相交于点D,点A为直线y=x上一点,过点A作AC⊥x轴于点C,交反比例函数y= (x>0)的图象于点B,连接BD.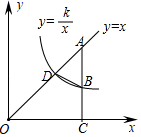 (1)、若点B的坐标为(8,2),则k= , 点D的坐标为;(2)、若AB=2BC,且△OAC的面积为18,求k的值及△ABD的面积.19. 如图1是一辆在平地上滑行的滑板车,如图2是其示意图.车杆 固定,车杆 可伸缩,车杆 长 ,车杆与脚踏板所成的角 ,前后轮子的半径均为 .
(1)、若点B的坐标为(8,2),则k= , 点D的坐标为;(2)、若AB=2BC,且△OAC的面积为18,求k的值及△ABD的面积.19. 如图1是一辆在平地上滑行的滑板车,如图2是其示意图.车杆 固定,车杆 可伸缩,车杆 长 ,车杆与脚踏板所成的角 ,前后轮子的半径均为 .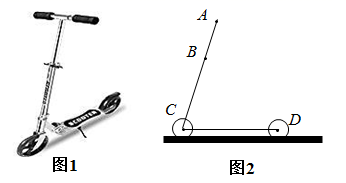 (1)、求固定车杆 的上端B离地面的高度(结果保留小数点后一位)(2)、小明站在滑板车上,双手放在把手A处最舒适,此时把手A离地面的高度为 ,求伸缩杆 的长度(结果保留小数点后一位;参考数据: )20. 如图,在平行四边形ABCD中,连接对角线AC , 延长AB至点E , 使 ,连接DE , 分别交BC , AC交于点F , G .
(1)、求固定车杆 的上端B离地面的高度(结果保留小数点后一位)(2)、小明站在滑板车上,双手放在把手A处最舒适,此时把手A离地面的高度为 ,求伸缩杆 的长度(结果保留小数点后一位;参考数据: )20. 如图,在平行四边形ABCD中,连接对角线AC , 延长AB至点E , 使 ,连接DE , 分别交BC , AC交于点F , G . (1)、求证: BF=CF ;
(1)、求证: BF=CF ;
(2)、若 , ,求FG的长.21. 如图, , , 三点在 上,直径 平分 ,过点 作 交弦 于点 ,在 的延长线上取一点 ,使得 .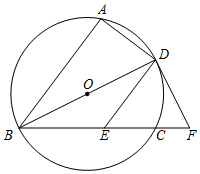 (1)、求证: 是 的切线;(2)、连接AF交DE于点M,若AD=4,DE=5,求DM的长.22. 观察猜想:(1)、如图1,在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D与点C重合,点E在斜边AB上,连接DE,且DE=AE,将线段DE绕点D顺时针旋转90°得到线段DF,连接EF,则 = , sin∠ADE= ,
(1)、求证: 是 的切线;(2)、连接AF交DE于点M,若AD=4,DE=5,求DM的长.22. 观察猜想:(1)、如图1,在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D与点C重合,点E在斜边AB上,连接DE,且DE=AE,将线段DE绕点D顺时针旋转90°得到线段DF,连接EF,则 = , sin∠ADE= ,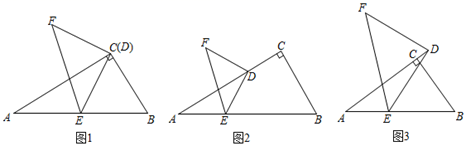 (2)、在(1)中,如果将点D沿CA方向移动,使CD= AC,其余条件不变,如图2,上述结论是否保持不变?若改变,请求出具体数值:若不变,请说明理由.
(2)、在(1)中,如果将点D沿CA方向移动,使CD= AC,其余条件不变,如图2,上述结论是否保持不变?若改变,请求出具体数值:若不变,请说明理由.拓展延伸
(3)、如图3,在△ABC中,∠ACB=90°,∠CAB=a,点D在边AC的延长线上,E是AB上任意一点,连接DE.ED=nAE,将线段DE绕着点D顺时针旋转90°至点F,连接EF.求 和sin∠ADE的值分别是多少?(请用含有n,a的式子表示)23. 已知抛物线 和抛物线 ( 为正整数). (1)、抛物线 与 轴的交点 , 顶点坐标;(2)、当 时,请解答下列问题.
(1)、抛物线 与 轴的交点 , 顶点坐标;(2)、当 时,请解答下列问题.①直接写出 与 轴的交点 , 顶点坐标 , 请写出抛物线 , 的一条相同的图象性质 ;
②当直线 与 , 相交共有4个交点时,求 的取值范围.
(3)、若直线 ( )与抛物线 ,抛物线 ( 为正整数)共有4个交点,从左至右依次标记为点 ,点 ,点 ,点 ,当 时,求出 , 之间满足的关系式.