陕西省武功县2021-2022学年九年级上学期数学10月质量检测试卷

试卷更新日期：2021-11-09 类型：月考试卷

进入出卷网下载

一、单选题

1. $- \frac{5}{4}$ 的相反数是（）

A、 $- \frac{4}{5}$ B、 $\frac{4}{5}$ C、 $- \frac{5}{4}$ D、 $\frac{5}{4}$

查看试题解析
2. 下列运算正确的是（　　）

A、 $a^{6} \div a^{3} = a^{3}$ B、 $a^{3} \cdot a^{2} = a^{6}$ C、 ${(- 3 a)}^{2} = - 6 a^{2}$ D、 $a^{2} + a^{2} = a^{4}$

查看试题解析
3. 如图，平行四边形ABCD中，对角线AC、BD相交于点O，则下列结论中不正确的是（　　）

A、当AB＝BC时，它是菱形 B、当AC⊥BD时，它是菱形 C、当AC＝BD时，它是矩形 D、当AC垂直平分BD时，它是正方形

查看试题解析
4. 用配方法解 $x^{2} - 8 x + 5 = 0$ 方程，将其化成 ${(x + a)}^{2} = b$ 的形式，则变形正确的是（）

A、 ${(x + 4)}^{2} = 11$ B、 ${(x - 4)}^{2} = 21$ C、 ${(x - 8)}^{2} = 11$ D、 ${(x - 4)}^{2} = 11$

查看试题解析
5. 如图，ABCD是矩形，AC、BD相较于O，AE垂直平分BO，若 $A E = 2 \sqrt{3}$ ，则 $O D =$ （）

A、2 B、3 C、4 D、6

查看试题解析
6. 在“支援河南洪灾”捐款活动中，某班级8名同学积极捐出自己的零花钱，奉献爱心，他们捐款的数额分别是（单位：元）：60，25，60，30，30，25，65，60.这组数据的众数和中位数分别是（　　）

A、60，30 B、30，30 C、25，45 D、60，45

查看试题解析
7. 若关于x的方程 $x^{2} - 2 x + m - 1 = 0$ 没有实数根，则m的取值范围是（）

A、 $m < 2$ B、 $m < - 2$ C、 $m > 2$ D、 $m > - 2$

查看试题解析
8. 如图，点E是 $△ A B C$ 内一点， $∠ A E B = 90 °$ ，D是边 $A B$ 的中点，延长线段 $D E$ 交边 $B C$ 于点F，点F是边 $B C$ 的中点，若 $A B = 6$ ， $E F = 1$ ，则线段 $A C$ 的长为（　　）

A、8 B、 $\frac{15}{2}$ C、7 D、9

查看试题解析

二、填空题

9. 因式分解： $9 a - 4 a^{3} =$ .

查看试题解析
10. 比较大小： $2 \sqrt{6}$ 5（选填“ $>$ ”、“ $=$ ”、“ $<$ ” ）．

查看试题解析
11. 第五套人民币中的5角硬币色泽为镍白色，正、反面的内周边缘均为正十一边形，则其内角和为.

查看试题解析
12. 若关于x的不等式 $2 x - a \leq 1$ 有2个正整数解，则a的取值范围为.

查看试题解析
13. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 3$ ， $B C = 4$ ，P为 $A B$ 上任意一点， $P F ⊥ A C$ 于点F， $P E ⊥ B C$ 于点E，则 $E F$ 的最小值是.

查看试题解析

三、解答题

14. 计算： $4 \times (- 3) + | - 8 | - \sqrt{9} + {(- \frac{1}{7})}^{- 1}$ .

查看试题解析
15. 解方程 $2 x^{2} - 7 x + 3 = 0$ .

查看试题解析
16. 如图，四边形 $A B C D$ 是平行四边形，且对角线 $A C$ ， $B D$ 交于点O， $B D = 2 A B$ ， $A E // B D$ ， $O E // A B$ .

求证：四边形 $A B O E$ 是菱形.

查看试题解析
17. 先化简，再求值： $(\frac{2 x^{2} + 2 x}{x^{2} - 1} - \frac{x^{2} - x}{x^{2} - 2 x + 1}) \div \frac{x}{x + 1}$ ，其中 $x = - 5$ .

查看试题解析
18. 如图，在平面直角坐标系中， $△ A B C$ 的顶点坐标分别为 $A (- 1 ， 0)$ ， $B (- 4 ， 1)$ ， $C (- 2 ， 2)$ .

（ 1 ）直接写出点B关于原点对称的点 $B'$ 的坐标：_▲_；

（ 2 ）平移 $△ A B C$ ，使平移后点A的对应点 $A_{1}$ 的坐标为 $(2 ， 1)$ ，请画出平移后的 $△ A_{1} B_{1} C_{1}$ ；

（ 3 ）画出 $△ A B C$ 绕原点O逆时针旋转 $90 °$ 后得到的 $△ A_{2} B_{2} C_{2}$ .

查看试题解析
19. 已知3是一元二次方程x²-2x+a=0的一个根，求a的值和方程的另一个根.

查看试题解析
20. 某校组织了一次防溺水、防交通事故、防食物中毒、防校园欺凌及其他各种安全意识的调查活动，了解同学们在哪些方面的安全意识薄弱，便于今后更好地开展安全教育活动.根据调查结果，绘制出图1，图2两幅不完整的统计图.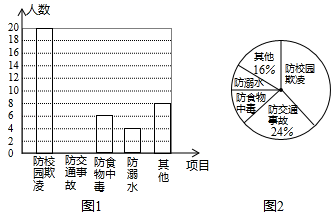

请结合图中的信息解答下列问题：

(1)、本次调查的人数为，其中防校园欺凌意识薄弱的人数占 $%$ ；

(2)、补全条形统计图；

(3)、该校共有1500名学生，请估计该校学生中防溺水意识薄弱的人数.

查看试题解析
21. 阅读材料，解答问题：
材料：∵ $\sqrt{4} < \sqrt{7} < \sqrt{9} ，$ 即 $2 < \sqrt{7} < 3$ ，∴ $\sqrt{7}$ 的整数部分为2，小数部分为 $\sqrt{7} - 2$ .

问题：已知 $5 a + 2$ 的立方根是3， $3 a + b - 1$ 的算术平方根是4，c是 $\sqrt{13}$ 的整数部分.

(1)、求 $\sqrt{13}$ 的小数部分.

(2)、求 $3 a - b + c$ 的平方根.

查看试题解析
22. 如图，在平行四边形ABCD中，点E是边BC的中点，连接AE并延长，交DC的延长线于点F，连接AC，BF.

(1)、求证：△ABE≌△FCE；

(2)、当四边形ABFC是矩形时，若∠AEC＝120°，求∠D的度数.

查看试题解析
23. 某生态柑橘园现有柑橘21吨，计划租用A、B两种型号的货车将柑橘运往外地销售.已知满载时，用3辆A型车和2辆B型车一次可运柑橘13吨；用4辆A型车和3辆B型车一次可运柑橘18吨.

(1)、1辆A型车和1辆B型车满载时一次分别运柑橘多少吨？

(2)、若计划租用，A型货车m辆，B型货车n辆，一次运完全部柑橘，且每辆车均为满载请帮柑橘园设计租车方案；

查看试题解析
24. 如图，在平行四边形 $A B C D$ 中，过点D作 $D E ⊥ A B$ 于点E，点F $F$ 在边 $C D$ 上，且 $F C = A E$ ，连接 $A F$ 、 $B F$ .

(1)、求证：四边形 $D E B F$ 是矩形；

(2)、若 $A F$ 平分 $∠ D A B$ ， $F C = 6$ ， $D F = 10$ ，求 $B F$ 的长.

查看试题解析
25. 如图，点G在正方形ABCD的边CD上，且四边形CEFG也是正方形，连接BG，DE，AF，取AF的中点M，连接CM.

求证：

(1)、 $B G = D E$ ；

(2)、 $C M = \frac{1}{2} A F$ .

查看试题解析
26. 民族要复兴，乡村必振兴2月21日发布的2021年中央一号文件，主题是全面推进乡村振兴加快农业农村现代化.乡村振兴战略的实施效果要用农民生活富裕水平来评价，某合作社为尽快打开市场，对本地新产品进行线上和线下销售相结合的模式，具体费用标准如下：
线下销售模式：标价5元/千克，八折出售；

线上销售模式：标价5元/千克，九折出售，超过6千克时，超出部分每千克再让利1.5元.

购买这种新产品x千克，所需费用为y元，y与x之间的函数关系如图所示.

根据以上信息回答下列问题：

(1)、请求出两种销售模式对应的函数解析式；

(2)、说明图中点C坐标的实际意义；

(3)、若想购买这种产品10千克，请问选择哪种模式购买最省钱？

查看试题解析