江西省赣州市赣县区2019-2020学年九年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 事件：“在只装有2个白球和5个黑球的袋子里，摸出一个红球”是（  ）
    A、可能事件 B、随机事件 C、不可能事件 D、必然事件

    查看试题解析

  • 2. 下列图案中，不是中心对称图形的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 3. 如图，AB是半圆O的直径，∠BAC＝40°，则∠D的度数是（    ）

    A、140° B、130° C、120° D、110°

    查看试题解析

  • 4. 若x1、x2是x2+x﹣1＝0方程的两个不相等的实数根，则x1+x2﹣x1x2的值为（  ）
    A、5 +1 B、5 ﹣2 C、﹣2 D、0

    查看试题解析

  • 5. 抛物线y＝x2＋4x＋3是由某个抛物线向左平移1个单位长度，再向下平移2个单位长度得到的，则原抛物线的解析式为（  ）
    A、y＝（x－2）2＋5 B、y＝（x＋2）2－1 C、y＝（x＋1）2＋1 D、y＝（x－1）2＋1

    查看试题解析

  • 6. 在平面直角坐标系中，若点E关于M的对称点为F，则点M是线段EF的中点．如图，已知A（1，﹣1），B（﹣1，﹣1），C（0，1），点P（0，2）关于A的对称点为P1 ， P1关于B的对称点为P2 ， P2关于C的对称点为P3 ， P3关于A的对称点为P4 ， …，则点P2019的坐标是（  ）

    A、（4，0） B、（﹣2，2） C、（2，﹣4） D、（﹣4，2）

    查看试题解析

二、填空题

  • 7. 已知 x=−1 是关于 x 的方程 2x2+ax−a=0 的一个根，则 a=

    查看试题解析

  • 8. 某毛绒玩具厂对一批毛绒玩具进行质量抽检，相关数据如下：

    抽取的毛绒玩具数 n

    20

    50

    100

    200

    500

    1000

    1500

    2000

    优等品的频数 m

    19

    47

    91

    184

    462

    921

    1379

    1846

    优等品的频率 mn

    0.950

    0.940

    0.910

    0.920

    0.924

    0.921

    0.919

    0.923

    从这批玩具中，任意抽取的一个毛绒玩具是优等品的概率的估计值是.（精确到 0.01)

    查看试题解析

  • 9. 如图，把△ABC绕点C顺时针旋转35°得到△A′B′C，A′B′交AC于点D，若A′D＝CD，则∠A＝度．

    查看试题解析

  • 10. 某工厂2017年产品的产量为100吨，该产品产量的年平均增长率为x（x＞0），设2019年该产品的产量为y吨，则y关于x的函数关系式为 ．

    查看试题解析

  • 11. 已知圆锥的母线长为 5cm ， 高为 4cm ， 则该圆锥侧面展开图的圆心角是 ．

    查看试题解析

  • 12. 已知矩形ABCD中，AB＝8，AD＝16，将它围绕顶点A逆时针旋转一周，旋转过程中B、C、D的对应点依次为E、F、G，连接DE，则当△ADE为直角三角形时，旋转角α（0°＜α＜360°）的大小为 ．

    查看试题解析

三、解答题

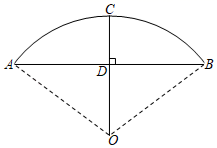
  • 13. 解方程：x2﹣4x＝0．

    查看试题解析

  • 14. 如图，已知弓形的弦长AB＝12，弓高CD＝2（CD⊥AB并经过圆心O）．求弓形所在⊙O的半径的长．

    查看试题解析

  • 15. 已知，在同一平面直角坐标系中，正比例函数y＝﹣2x与二次函数y＝﹣x2+2x+c的图象交于点A（﹣1，m）．
    (1)、求m，c的值；
    (2)、求二次函数图象的对称轴和顶点坐标．

    查看试题解析

  • 16. 一个不透明的口袋里装有分别标有汉字“幸”、“福”、“赣”、“县”的四个小球，除汉字不同之外，小球没有任何区别．
    (1)、若从袋中任取一个球，球上的汉字刚好是“福”的概率为；
    (2)、若同时从袋中任取两个球，记取出的两个球上的汉字恰能组成“幸福”或“赣县”为事件A，请用列表或画树状图的方法求出事件A的概率．

    查看试题解析

  • 17. 如图， AB 是 ⊙O 中不过圆心的一条弦，请仅用无刻度的直尺，分别按下列要求画图．

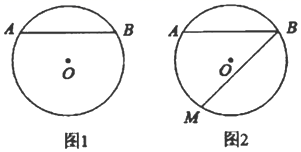    (1)、在图1中画出一条弦 CD 使 CD//AB ；
    (2)、在图2中， M 是 AB 下方 ⊙O 上的一点，以点 A ， M 为顶点画一个直角三角形，使其第三个顶点也落在 ⊙O 上，并使该直角三角形的一个内角与 ∠ABM 相等．

    查看试题解析

  • 18. 某商场销售一批衬衫，平均每天可销售出20件，每件盈利40元，为扩大销售盈利，商场决定采取适当的降价措施，但要求每件盈利不少于20元，经调查发现．若每件衬衫每降价1元，则商场每天可多销售2件．
    (1)、若每件衬衫降价4元，则每天可盈利多少元？
    (2)、若商场平均每天盈利1200元．则每件衬衫应降价多少元？

    查看试题解析

  • 19. 在平面直角坐标系中，四边形ABCD的位置如图所示，请解答下列问题：

    (1)、将四边形ABCD先向左平移5个单位，再向下平移5个单位，得到四边形A1B1C1D1 ， 画出平移后的四边形A1B1C1D1；
    (2)、将四边形A1B1C1D1绕点A1逆时针旋转90°，得到四边形A1B2C2D2 ， 画出旋转后的四边形A1B2C2D2 ， 并写出点C2的坐标．
    (3)、判断四边形A1B2C2D2是否可以看成由四边形ABCD绕着某点旋转一定角度所得，如果是，请直接写出这点的坐标；如果不是，请说明理由．

    查看试题解析

  • 20. 如图，AB是⊙O的直径，延长弦BC到点D，使得CD＝BC，AD交⊙O于点E，连接BE．

    (1)、求证：AB＝AD；
    (2)、若AB＝8，∠DBE＝22.5°，求阴影部分的面积．

    查看试题解析

  • 21. 创建文明城市，让老百姓住得更舒心，某社区决定把一块长50m，宽30m的矩形空地建成居民健身广场，设计方案如图，阴影部分为四个全等的矩形绿化区，剩余区域为活动区，且四周的出口宽度相同（其宽度不小于14m），设绿化区较长边为xm，活动区的面积为ym2 ．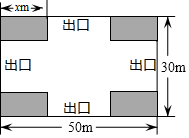

    (1)、请用含x的代数式表示矩形绿化区另一边长，并求出y与x的函数关系式（不要求写出自变量x的取值范围）；
    (2)、预计活动区造价为50元/m2 ， 绿化区造价为40元/m2 ， 若社区的此项建造投资费用不得超过72000元，求绿化区较长边x的取值范围．

    查看试题解析

  • 22. 如图，在Rt△ABC中，∠ACB＝90°，以点B为圆心，BC长为半径画弧，交边AB与点D，连接CD．

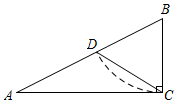    (1)、若∠A＝28°，求∠ACD的度数；
    (2)、若BC＝1，AC＝a．

    ①直接写出线段AD的长为（用含字母a的式子表示）；

    ②判断线段AD的长是方程x2+2x﹣a2＝0的一个根吗？为什么？

    查看试题解析

  • 23. 我们知道，二次函数y＝a（x﹣h）2+k（a≠0）的图象是一条抛物线，现定义一种变换，先作这条抛物线关于原点对称的抛物线y′，再将抛物线y′向上平移m（m＞0）个单位，得到新的抛物线ym ， 我们称ym叫做二次函数y＝a（x﹣h）2+k（a≠0）的m阶变换．
    (1)、已知：二次函数y＝2（x+2）2+1，它的顶点关于原点的对称点为 ， 这个抛物线的2阶变换的表达式为 ．
    (2)、若二次函数M的6阶变换的关系式为y6＝（x﹣1）2+5．

    ①二次函数M的函数表达式为 ．

    ②若二次函数M的顶点为点A，与x轴相交的两个交点中左侧交点为点B，动点P在抛物线y6上，作PD⊥直线AB，请求出PD最小时P点的坐标 ．

    查看试题解析

  • 24. 如图①，已知△ABC是等腰直角三角形，∠BAC＝90°，点D是BC的中点．作正方形DEFG，使点A，C分别在DG和DE上，连接AE，BG．

    (1)、试猜想线段BG和AE的数量关系，请直接写出你得到的结论；
    (2)、将正方形DEFG绕点D逆时针方向旋转一定角度后（旋转角度大于0°，小于或等于360°），如图②，通过观察或测量等方法判断（1）中的结论是否仍然成立？如果成立，请予以证明；如果不成立，请说明理由；
    (3)、若BC＝DE＝2，在（2）的旋转过程中，当AE为最大值时，求AF的值．

    查看试题解析