江西省赣州市大余县2020-2021学年九年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 下列图形中，既是中心对称图形又是轴对称图形的是（    ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 抛物线 y=(x−1)2−4 的顶点为（    ）
    A、（1，4） B、（1，-4） C、（-1，4） D、（-1，-4）

    查看试题解析

  • 3. 下列事件中，是必然事件的是 （     ）
    A、任意抛一枚硬币，正面朝上 B、随意翻开一本数学书，这页的页码是偶数 C、相等的圆心角所对的弧也相等 D、任意画一个圆内接四边形，其对角互补

    查看试题解析

  • 4. 已知⊙O的半径是一元二次方程 x2−6x+9=0 的解，且点O到直线AB的距离为2，则⊙O与直线AB的位置关系为（    ）
    A、相交 B、相切 C、相离 D、无法确定

    查看试题解析

  • 5. 如图，学校课外生物小组的试验园地是长20米，宽15米的长方形.为了便于管理，现要在中间开辟一横两纵等宽的小道（如图），要使种植面积为252平方米，则小道的宽为（   ）

    A、5米 B、1米 C、2米 D、3米

    查看试题解析

  • 6. 若抛物线 y=−x2+px+q 与 x 轴交于A（a，0）、B（b，0）两点，且 a<1<b ，则有（    ）
    A、p+q<1 B、p+q=1 C、p+q>1 D、pq>0

    查看试题解析

二、填空题

  • 7. 已知点P（-3，2）关于原点的对称点是 ．

    查看试题解析

  • 8. 已知：如图，圆锥的底面直径是10cm，高为12cm，则它的侧面展开图的面积是cm2 ．

     

    查看试题解析

  • 9. 如图，点A，B，C在⊙O上，CO的延长线交AB于点D，∠A=50°，∠B=30°，则∠ADC的度数为 ．

    查看试题解析

  • 10. 将抛物线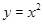 向左平移2个单位长度，再向下平移3个单位长度，得到的抛物线的函数表达式为 ．

    查看试题解析

  • 11. 已知 x1、x2 是方程 x2−3x−1=0 的根，则式子 x12−2x1+x2 的值为 ．

    查看试题解析

  • 12. 已知⊙O 的直径为 4，AB 是⊙O 的弦，∠AOB=120°，点 P 在⊙O 上，若点 P到直线 AB 的距离为 1，则∠PAB 的度数为 ．

    查看试题解析

三、解答题

  • 13. 计算：
    (1)、x2−x−6＝0 ；
    (2)、(x−5)2＝2(x−5) ．

    查看试题解析

  • 14. 在直角坐标系中，O为原点，A点的坐标为（3，4），连接线段OA，将线段OA绕点O逆时针旋转90°，A的对应点为A′．

    (1)、请在图中画出线段OA和线段OA′，则A′的坐标为 ．
    (2)、求线段OA在旋转过程中所扫过的面积．

    查看试题解析

  • 15. 如图，AB为⊙O的直径，C，D为圆上的两点，OC∥BD，弦AD，CO相交于点E．

    (1)、求证： AC⌢=CD⌢ ；
    (2)、若AD=16，CE=4，求⊙O的半径．

    查看试题解析

  • 16. 今年我县为创评“全国文明城市”称号，周末团委组织志愿者进行宣传活动．班主任梁老师决定从4名女班干部（小悦、小惠、小艳和小倩）中通过抽签方式确定2名女生去参加．抽签规则：将4名女班干部姓名分别写在四张完全相同的卡片正面，把四张卡片背面朝上，洗匀后放在桌面上，梁老师先从中随机抽取一张卡片，记下姓名，再从剩余的三张卡片中随机抽取第二张，记下姓名．
    (1)、该班男生“小刚被抽中”是事件（填“不可能”“必然”“随机”）；第一次抽取卡片“小悦被抽中”的概率为 ．
    (2)、试用画树状图或列表的方法表示这次抽签所有可能的结果，求出“小惠被抽中”的概率．

    查看试题解析

  • 17. 如图，△ABC内接于⊙O，AB＝AC，D是AC弧的中点，在下列图中使用无刻度的直尺按要求画图．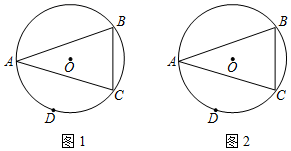

    (1)、在图1中，画出△ABC中AC边上的中线；
    (2)、在图2中，画出△ABC中AB边上的中线．

    查看试题解析

  • 18. 大润发超市进了一批成本为8元/个的文具盒．调查发现：这种文具盒每个星期的销售量y（个）与它的定价x（元/个）的关系如图所示：

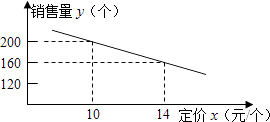    (1)、求这种文具盒每个星期的销售量y（个）与它的定价x（元/个）之间的函数关系式（不必写出自变量x的取值范围）；
    (2)、每个文具盒定价是多少元时，超市每星期销售这种文具盒（不考虑其他因素）可获得的利润最高？最高利润是多少？

    查看试题解析

  • 19. 如图，在直角坐标系中，点A的坐标为（-2，0），OB=OA，且∠AOB=120°．

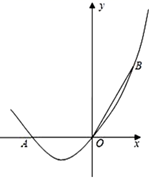    (1)、求直线AB的解析式；
    (2)、经过A、O、B三点的抛物线的对称轴上是否存在点C，使△BOC的周长最小?若存在，求出点C的坐标；若不存在，请说明理由．

    查看试题解析

  • 20. 如图，AB是以BC为直径的半圆O的切线，D为半圆上一点，AD＝AB，AD、BC的延长线相交于点E．

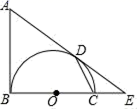    (1)、求证：AD是半圆O的切线；
    (2)、连结CD，求证：∠A＝2∠CDE．

    查看试题解析

  • 21. 已知关于x的一元二次方程（a+c）x2+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长．
    (1)、如果x=﹣1是方程的根，试判断△ABC的形状，并说明理由；
    (2)、如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
    (3)、如果△ABC是等边三角形，试求这个一元二次方程的根．

    查看试题解析

  • 22. 如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°．若固定△ABC，将△DEC绕点C旋转．

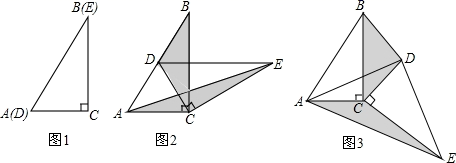    (1)、当△DEC统点C旋转到点D恰好落在AB边上时，如图2．

    ①当∠B=∠E=30°时，此时旋转角的大小为；

    ②当∠B=∠E=α时，此时旋转角的大小为（用含a的式子表示）．

    (2)、当△DEC绕点C旋转到如图3所示的位置时，小杨同学猜想：△BDC的面积与△AEC的面积相等，试判断小杨同学的猜想是否符合题意，若符合题意，请你证明小杨同学的猜想．若不符合题意，请说明理由．

    查看试题解析

  • 23. 如图，二次函数 y=−x2+3x+m 的图象与x轴的一个交点为B（4，0），另一个交点为A，且与y轴相交于C点．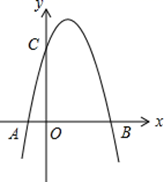

     

    (1)、求m的值及C点坐标；
    (2)、P为抛物线上一点，它关于直线BC的对称点为Q．

    ①当四边形PBQC为菱形时，求点P的坐标；

    ②点P的横坐标为t（0＜t＜4），当t为何值时，四边形PBQC的面积最大，请说明理由．

    查看试题解析