湖北省武汉市武汉六初、六中上智2021-2022学年九年级上学期数学9月月考试卷
试卷更新日期:2021-11-09 类型:月考试卷
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、三角形 B、等边三角形 C、平行四边形 D、菱形2. 一元二次方程2x2=x﹣3的二次项系数和常数项分别是( )A、2,﹣1 B、2,3 C、﹣1,3 D、﹣1,23. 已知m是一元二次方程x2﹣4x+1=0的一个根,则2021﹣m2+4m的值为( )A、﹣2021 B、2021 C、2020 D、20224. 抛物线y=﹣2x2经过平移后得到y=﹣2(x+3)2﹣4,其平移方法是( )A、向右平移3个单位,再向下平移4个单位 B、向右平移3个单位,再向上平移4个单位 C、向左平移3个单位,再向下平移4个单位 D、向左平移3个单位,再向上平移4个单位5. 如图,在△ABC中,∠B=55°,∠ACB=30°,将△ABC绕点C顺时针旋转n度(0<n<180)得到△EDC,若CE∥AB,则n的值为( )
 A、65 B、90 C、95 D、1256. 某种细胞分裂,一个细胞经过两轮分裂后,共有a个细胞,设每轮分裂中平均一个细胞分裂成x个细胞,那么可列方程为( )A、x2=a B、(1+x)2=a C、1+x+x2=a D、x+x2=a7. 已知二次函数y=3(x﹣1)2+h的图象上有三点,A(﹣0.5,y1),B(2.5,y2),C(3,y3),则y1 , y2 , y3的大小关系为( )A、y1=y2<y3 B、y1<y2<y3 C、y1<y2=y3 D、y3<y1=y28. 在同一平面直角坐标系中,一次函数y=kx﹣1与二次函数y=kx2+3的大致图象可以是( )A、
A、65 B、90 C、95 D、1256. 某种细胞分裂,一个细胞经过两轮分裂后,共有a个细胞,设每轮分裂中平均一个细胞分裂成x个细胞,那么可列方程为( )A、x2=a B、(1+x)2=a C、1+x+x2=a D、x+x2=a7. 已知二次函数y=3(x﹣1)2+h的图象上有三点,A(﹣0.5,y1),B(2.5,y2),C(3,y3),则y1 , y2 , y3的大小关系为( )A、y1=y2<y3 B、y1<y2<y3 C、y1<y2=y3 D、y3<y1=y28. 在同一平面直角坐标系中,一次函数y=kx﹣1与二次函数y=kx2+3的大致图象可以是( )A、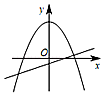 B、
B、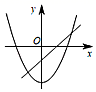 C、
C、 D、
D、 9. 在平面直角坐标系中,一个蜘蛛最初在点A(p,0)(p是常数,且p>1),第一次爬到射线OA绕O点逆时针旋转60°方向上的A1点,且OA1=pOA;第二次爬到射线OA1绕O点逆时针旋转60°方向上的A2点,且OA2=pOA1;…;第2021次爬行到A2021点的坐标是( )
9. 在平面直角坐标系中,一个蜘蛛最初在点A(p,0)(p是常数,且p>1),第一次爬到射线OA绕O点逆时针旋转60°方向上的A1点,且OA1=pOA;第二次爬到射线OA1绕O点逆时针旋转60°方向上的A2点,且OA2=pOA1;…;第2021次爬行到A2021点的坐标是( )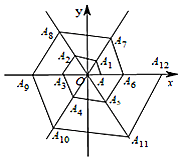 A、(p2021 , 0) B、 C、(﹣p2021 , 0) D、10. 当m≤x≤m+1时,函数y=x2﹣4|x|+2的最大值为2,则m满足的条件为( )A、﹣1<m≤0 B、m=﹣4或3或﹣1≤m≤0 C、m=﹣4或﹣1<m≤0 D、m=﹣4或3
A、(p2021 , 0) B、 C、(﹣p2021 , 0) D、10. 当m≤x≤m+1时,函数y=x2﹣4|x|+2的最大值为2,则m满足的条件为( )A、﹣1<m≤0 B、m=﹣4或3或﹣1≤m≤0 C、m=﹣4或﹣1<m≤0 D、m=﹣4或3二、填空题
-
11. 在平面直角坐标系中,点P(﹣3,1)关于坐标原点中心对称的点P′的坐标是.12. 抛物线y=-x2+2x+2的顶点坐标是 .
13. 二次函数y=kx2﹣3x+1的图象与x轴有公共点,则常数k的取值范围是.14. 飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是 ,飞机着陆至停下来共滑.15. 已知二次函数y=ax2+bx+c(a≠0)的的部分图象如图,图象经过(﹣1,0),对称轴为x=2.下列4个结论:①4a+b=0;②9a+c>3b;③一元二次方程cx2+bx+a=0两根为﹣1和 ;④不等式a(x+1)(x﹣5)<﹣3的解集满足x<﹣1或x>5.其中正确的结论序号是. 16. 如图,在△ABC中,∠BAC=120°,AB+AC=a(a>0),将CB绕C顺时针旋转120°得CD,当DA长的最小值为 时,a的值为.
16. 如图,在△ABC中,∠BAC=120°,AB+AC=a(a>0),将CB绕C顺时针旋转120°得CD,当DA长的最小值为 时,a的值为.
三、解答题
-
17. 解方程:(1)、x2+2x=0;(2)、4x2﹣x﹣9=0.18. 如图,利用一面墙(墙的长度不限),用 长的篱笆,怎样围成一个面积为 的矩形场地?
 19. 已知关于x的一元二次方程x2﹣2kx+k2+k=0有实数根.(1)、求k的取值范围;(2)、设此方程的两个根分别为x1 , x2 , 若x12+x22+3x1x2=6,求k的值.20. 如图所示,在由边长为1的小正方形组成的正方形网格中建立平面直角坐标系,格点 ABC的顶点坐标分别为A(1,4)、B(6,4)、C(2,0),请仅用无刻度直尺,在给定的网格中依次完成下列作图(要求保留必要的作图痕迹),并回答下列问题:
19. 已知关于x的一元二次方程x2﹣2kx+k2+k=0有实数根.(1)、求k的取值范围;(2)、设此方程的两个根分别为x1 , x2 , 若x12+x22+3x1x2=6,求k的值.20. 如图所示,在由边长为1的小正方形组成的正方形网格中建立平面直角坐标系,格点 ABC的顶点坐标分别为A(1,4)、B(6,4)、C(2,0),请仅用无刻度直尺,在给定的网格中依次完成下列作图(要求保留必要的作图痕迹),并回答下列问题:
( 1 )在AB上找点E,使∠ACE=45°.
( 2 )点A关于直线BC的对称点为D,在BD上找点F,使BF=BE.
( 3 )将线段AC绕点Q逆时针方向旋转90°得到线段BH,使点C的对应点为点B,画出线段BH,并写出点Q的坐标.
21. 如图,抛物线 与直线 交于A、B两点. (1)、直接写出当y1<y2时,自变量x的取值范围.(2)、点C在抛物线上,点D在直线AB上,当四边形AODC是平行四边形时,求点C的横坐标.22. 某宾馆有50间相同的客房,当房间的定价为每天180元时,房间会全部住满.统计表明:当房价每上调10元时,就会有一个房间空闲,宾馆需对有客人居住的房间每天支出20元的各种费用.设该宾馆房价上调x元(x为10的正整数倍)时,相应的住房数为y间.(1)、求y与x的函数关系式.(2)、房价为多少时,宾馆的利润最大?最大利润是多少?(3)、若老板决定每住进去一间房就捐出a元(0<a≤40)给当地福利院,同时要保证房间定价在180元至360元之间波动时(包括两端点),利润随x的增大而增大,求a的取值范围.23. 在△ABE和△CDE中,∠ABE=∠DCE=90°,AB=BE,CD=CE.
(1)、直接写出当y1<y2时,自变量x的取值范围.(2)、点C在抛物线上,点D在直线AB上,当四边形AODC是平行四边形时,求点C的横坐标.22. 某宾馆有50间相同的客房,当房间的定价为每天180元时,房间会全部住满.统计表明:当房价每上调10元时,就会有一个房间空闲,宾馆需对有客人居住的房间每天支出20元的各种费用.设该宾馆房价上调x元(x为10的正整数倍)时,相应的住房数为y间.(1)、求y与x的函数关系式.(2)、房价为多少时,宾馆的利润最大?最大利润是多少?(3)、若老板决定每住进去一间房就捐出a元(0<a≤40)给当地福利院,同时要保证房间定价在180元至360元之间波动时(包括两端点),利润随x的增大而增大,求a的取值范围.23. 在△ABE和△CDE中,∠ABE=∠DCE=90°,AB=BE,CD=CE.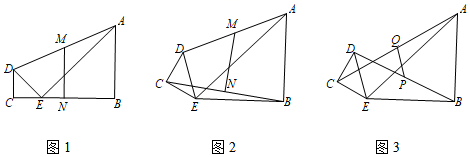 (1)、连接AD、BC,点M、N分别为AD、BC的中点,连接MN,
(1)、连接AD、BC,点M、N分别为AD、BC的中点,连接MN,①如图1,当B、E、C三点在一条直线上时,MN与BC关系是 .
②如图2,当等腰Rt△CDE绕点E顺时针旋转时,①中的结论还成立吗?如果成立,请证明你的结论;如果不成立,请说明理由.
(2)、如图3,当等腰Rt△CDE绕点E顺时针旋转时,连接AC、BD,点P、Q分别为BD、AC的中点,连接PQ,若AB=13,CD=5,则PQ的最大值时,此时以A、B、C、D为顶点的四边形的面积为 .24. 已知抛物线与x轴交于点A、点B,与y轴交于点C(0,3),顶点坐标(﹣2,﹣1). (1)、求抛物线的解析式.(2)、如图1,点D在第二象限的抛物线上,且∠CBO=∠CBD,求点D的坐标.(3)、如图2,将抛物线平移至顶点与原点重合得到新抛物线,M、N在新抛物线上且M在N的左侧,过M、N的两条直线与抛物线均有唯一的公共点,且两条直线交于点E,过E作EF∥y轴交MN于F,交抛物线于G,求证:G是EF中点.
(1)、求抛物线的解析式.(2)、如图1,点D在第二象限的抛物线上,且∠CBO=∠CBD,求点D的坐标.(3)、如图2,将抛物线平移至顶点与原点重合得到新抛物线,M、N在新抛物线上且M在N的左侧,过M、N的两条直线与抛物线均有唯一的公共点,且两条直线交于点E,过E作EF∥y轴交MN于F,交抛物线于G,求证:G是EF中点.