贵州省遵义市2021-2022学年九年级上学期数学第一次月考试卷

试卷更新日期：2021-11-09 类型：月考试卷

进入出卷网下载

一、单选题

1. 若方程 $(m - 1) x^{m^{2} + 1} + 3 x + 5 = 0$ 是一元二次方程，则m的值等于（）

A、±1 B、1 C、﹣1 D、0

查看试题解析
2. 把方程x²+2x＝5（x﹣2）化成ax²+bx+c＝0的形式，则a ， b ， c的值分别为（）

A、1，﹣3，2 B、1，7，﹣10 C、1，﹣5，12 D、1，﹣3，10

查看试题解析
3. 若 $x = - 1$ 是关于 $x$ 的一元二次方程 $a x^{2} + b x - 1 = 0$ 的一个根，则 $2021 + 3 a - 3 b$ 的值为（）

A、 $2018$ B、 $2020$ C、 $2022$ D、 $2024$

查看试题解析
4. 方程 $x^{2} = 4$ 的根为（）

A、 $x = 2$ B、 $x = - 2$ C、 $x = 0$ D、 $x = \pm 2$

查看试题解析
5. 用配方法解方程 $x^{2} + 4 x - 5 = 0$ 时，原方程应变形为（　　）

A、 ${(x - 2)}^{2} = 1$ B、 ${(x - 4)}^{2} = 11$ C、 ${(x + 2)}^{2} = 9$ D、 ${(x + 4)}^{2} = 21$

查看试题解析
6. 用公式法解方程 $x^{2} - 6 x + 1 = 0$ 所得的解正确的是（）

A、 $x = - 3 \pm \sqrt{10}$ B、 $x = 3 \pm \sqrt{10}$ C、 $x = - 3 \pm 2 \sqrt{2}$ D、 $x = 3 \pm 2 \sqrt{2}$

查看试题解析
7. 已知一元二次方程x²﹣10x＋24＝0的两个根是菱形的两条对角线长，则这个菱形的面积为（）

A、6 B、10 C、12 D、24

查看试题解析
8. 已知实数x满足（x²﹣2x+1）²+4 （x²﹣2x+1）﹣5＝0，那么x²﹣2x+1的值为（）

A、﹣5或1 B、﹣1或5 C、1 D、5

查看试题解析
9. 若m、n是一元二次方程x²+2x﹣2021＝0的两个实数根，则2m+2n﹣mn的值为（　　）

A、2021 B、2019 C、2017 D、2015

查看试题解析
10. 抛物线 $y = {(x + 1)}^{2} - 4 (- 2 \leq x \leq 2)$ ，如图所示，则函数y的最小值和最大值分别是（）

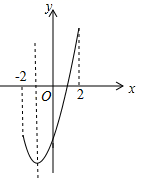A、-3和5 B、-4和5 C、-4和-3 D、-1和5

查看试题解析
11. 已知直线y＝kx与抛物线y＝ax²＋bx＋c在坐标系中如图所示， $m_{1}$ 和 $m_{2}$ 是方程ax²＋（b－k）x＋c＝0的两个根，且 $m_{1}$ ＞ $m_{2}$ ，则函数y＝ $m_{1}$ x＋ $m_{2}$ 在坐标系中的图象大致为（）

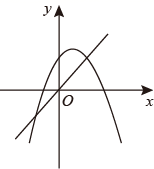A、 B、 C、 D、

查看试题解析
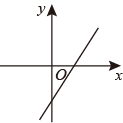12. 正方形ABCD中，AB=4，P为对角线BD上一动点，F为射线AD上一点，若AP=PF，则△APF的面积最大值为（）

A、8 B、6 C、4 D、 $2 \sqrt{2}$

查看试题解析

二、填空题

13. 二次函数 $y = {(x - 4)}^{2} - 5$ 的顶点坐标是.

查看试题解析
14. 2021年2月25日上午，习近平总书记在全国脱贫攻坚总结表彰大会上庄严宣告：历经8年艰苦努力，我国脱贫攻坚战取得了全面胜利，现行标准下9899万农村贫困人口全部脱贫，832个贫困县全部摘帽，12.8万个贫困村全部出列，区域性整体贫困得到解决.用科学记数法表示9899万人为人.

查看试题解析
15. 若使代数式 $\frac{\sqrt{2 - x}}{x}$ 有意义，则x的取值范围是．

查看试题解析
16. 如图1，正方形 $A B C D$ 中，点E为 $A B$ 的中点，连接 $C E$ ，动点P从A点出发，沿 $A B - B C - C D$ 运动，同时，动点Q从A点出发，沿 $A D$ 向点D运动，P，Q两点同时到达点D，设点P的运动时间为 $x (s)$ ， $△ A P Q$ 的面积为 $y ({cm}^{2})$ ，则y关于x的函数图象如图2，当 $△ A P Q$ 与 $△ C B E$ 全等时， $D P$ 的长为cm.

查看试题解析

三、解答题

17. 计算： $\sqrt{16} - (- 3) + {(π - 3.14)}^{0} - {(\frac{1}{3})}^{- 1}$ .

查看试题解析
18. 先化简： $(\frac{2 x}{x - 1} - \frac{x}{x + 1}) \div \frac{x}{x^{2} - 1}$ ，再从不等式组 ${\begin{array}{l} x - 2 (x - 1) \geq 1 \\ 6 x + 10 > 3 x + 1 \end{array}$ 的解集中取一个合适的整数值代入求值.

查看试题解析
19. 解方程：

(1)、x²+6x＝9；

(2)、3x（x﹣3）＝3﹣x；

(3)、 $\frac{6}{x + 1}$ ＝ $\frac{x + 5}{x (x + 1)}$ ；

(4)、 $\frac{4 x}{1 - x^{2}}$ +2＝ $\frac{2 x}{x + 1}$ .

查看试题解析
20. 某商店以每件40元的价格进了一批商品，出售价格经过两个月的调整，从每件50元上涨到每件72元，此时每月可售出188件商品.

(1)、求该商品平均每月的价格增长率；

(2)、因某些原因，商家需尽快将这批商品售出，决定降价出售.经过市场调查发现：售价每下降一元，每个月多卖出一件，设实际售价为x元，则x为多少元时销售此商品每月的利润可达到4000元.

查看试题解析
21. 已知关于x的一元二次方程x²﹣2（m﹣1）x+m²＝0有实数根.

(1)、求m的取值范围；

(2)、设此方程的两个根分别为x₁ ， x₂ ，若x₁²+x₂²＝8﹣3x₁x₂ ，求m的值.

查看试题解析
22. 在平面直角坐标系中，已知抛物线C：y＝ax²＋2x﹣1（a≠0）和直线l：y＝kx＋b，点A（﹣3，﹣3），B（1，﹣1）均在直线l上.

(1)、求出直线l的解析式；

(2)、当a＝﹣1，二次函数y＝ax²＋2x﹣1的自变量x满足m≤x≤m＋2时，函数y的最大值为﹣4，求m的值；

(3)、若抛物线C与线段AB有两个不同的交点，求a的取值范围.

查看试题解析
23. 路桥区某水产养殖户利用温棚养殖技术养殖南美白虾，与传统养殖相比，可延迟养殖周期，并从原来的每年养殖两季提高至每年三季.已知每千克白虾的养殖成本为8元，在某上市周期的70天里，销售单价p（元/千克）与时间第t（天）之间的函数关系如下： $p = {\begin{array}{l} \frac{1}{4} t + 20 ， (1 \leq t \leq 40 ， t 为整数) \\ - \frac{1}{2} t + 50 ， (40 < t \leq 70 ， t 为整数) \end{array}$ ，日销售量y（千克）与时间第t（天）之间的函数关系如图所示：

(1)、求日销售量y与时间t的函数关系式；

(2)、求第几天的日销售利润最大？最大利润是多少元？

(3)、在实际销售的前40天中，该养殖户决定每销售1千克白虾，就捐赠 $m (m < 8)$ 元给公益事业.在这前40天中，已知每天扣除捐赠后的日销售利润随时间t的增大而增大，求m的取值范围.

查看试题解析
24. 如图，在△ABC中，∠B＝90°，AB＝12cm，BC＝24cm，动点P从点A开始沿边AB向点B以2cm/s的速度移动，动点Q从点B开始沿边BC向点C以4cm/s的速度移动，如果P、Q两点分别从A，B两点同时出发，设运动时间为t，

(1)、AP＝， BP＝， BQ＝；

(2)、t为何值△时△PBQ的面积为32cm²？

(3)、t为何值时△PBQ的面积最大？最大面积是多少？

查看试题解析