内蒙古自治区赤峰市喀喇沁旗2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-05 类型：期末考试

进入出卷网下载

一、单选题

1. 运用图腾解释神话、民俗民风等是人类历史上最早的一种文化现象.下列图腾中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在三角形内部，且到三角形三边距离相等的点是（　　）

A、三角形三条中线的交点 B、三角形三条高线的交点 C、三角形三条角平分线的交点 D、三角形三边垂直平分线的交点

查看试题解析
3. 如果一个多边形的内角和等于它的外角和的3倍，则这个多边形是（　　）

A、三角形 B、四边形 C、六边形 D、八边形

查看试题解析
4. 对于① $x - 3 x y = x (1 - 3 y)$ ，② $(x + 3) (x - 1) = x^{2} + 2 x - 3$ ，从左到右的变形，表述正确的是（）

A、都是因式分解 B、都是乘法运算 C、①是因式分解，②是乘法运算 D、①是乘法运算，②是因式分解

查看试题解析
5. 下列运算中正确的是（）

A、 $\frac{x^{6}}{x^{3}} = x^{2}$ B、 $\frac{- x + y}{x + y} = - 1$ C、 $\frac{a^{2} + 2 a b + b^{2}}{a^{2} - b^{2}} = \frac{a + b}{a - b}$ D、 $\frac{x + 1}{y + 1} = \frac{x}{y}$

查看试题解析
6. 我国古代著作《四元玉鉴》记载“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽．每株脚钱三文足，无钱准与一株椽．“其大意为：现请人代买一批椽，这批椽的价钱为6210文．如果每件椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问6210文能买多少株椽？设这批椽的数量为 $x$ 株，则正确的方程是（）

A、 $3 (x - 1) = \frac{6210}{x}$ B、 $\frac{6210}{x - 1} = 3$ C、 $3 x - 1 = \frac{6210}{x}$ D、 $\frac{6210}{x} = 3$

查看试题解析
7. 如图， $D E / / A B ， ∠ C A E = \frac{1}{3} ∠ C A B ， ∠ C D E = 75^{\circ} ，$ $∠ B = 65^{\circ}$ ，则 $∠$ AEB=（）．

A、 $70^{\circ}$ B、 $65^{\circ}$ C、 $60^{\circ}$ D、 $55^{\circ}$

查看试题解析
8. 如图，AB=AC，点D，E分别在AB，AC上，补充下列一个条件后，不能判断△ABE ≌△ACD的是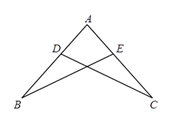

A、∠B=∠C B、AD=AE C、∠BDC=∠CEB D、BE=CD

查看试题解析
9. 利用图形中面积的等量关系可以得到某些数学公式．根据如图能得到的数学公式是（）

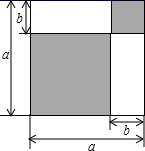A、（a+b）（a-b）=a²-b² B、（a-b）²=a²-2ab+b² C、a（a+b）=a²+ab D、a（a-b）=a²-ab

查看试题解析
10. 如图， $△ A B C$ 是等边三角形， $A D$ 是 $B C$ 边上的高，E是 $A C$ 的中点，P是 $A D$ 上的一个动点，当 $P C$ 与 $P E$ 的和最小时， $∠ E C P$ 的度数是（）

A、 $30^{°}$ B、 $45^{°}$ C、 $60^{°}$ D、 $90^{°}$

查看试题解析

二、填空题

11. 分解因式：x²(x＋y)＋2xy(x＋y)＋y² (x＋y)＝．

查看试题解析
12. 若关于 x 的方程 $\frac{x - 3}{x - 2} = \frac{m}{2 - x}$ 无解，则 m＝．

查看试题解析
13. 计算： ${(- 2 \frac{1}{5})}^{2019} \times {(\frac{5}{11})}^{2020}$ ＝．

查看试题解析
14. 如图，△ABC 是边长为 6 的等边三角形，D 是 BC 上一点，BD=2，DE⊥BC 交AB 于点 E，则 AE= ．

查看试题解析
15. 如图，已知△ABC的周长是18，OB、OC分别平分∠ABC和∠ACB ， OD⊥BC于D ，且OD＝1，△ABC的面积是．

查看试题解析
16. 如图，小明在操场上从A点出发，沿直线前进5米后向左转40°，再沿直线前进5米后，又向左转40°，照这样走下去，他第一次回到出发地A点时，一共走了米．

查看试题解析
17. 如图，在△ABC和△DBC中，∠ACB=∠DBC=90°，E是BC的中点，DE⊥AB，垂足为F，AB=DE．若BD=8cm，则AC的长为．

查看试题解析
18. A，B两地相距180km，新修的高速公路开通后，在A，B两地间行驶的长途客车平均车速提高了 50%，而从A地到B地的时间缩短了 1h .若设原来的平均车速为xkm/h ，则根据题意可列方程为 .

查看试题解析

三、解答题

19.

(1)、已知a+b＝5，ab＝10，求 $\frac{1}{2} a^{3} b + a^{2} b^{2} + \frac{1}{2} a b^{3}$ 的值．

(2)、解分式方程： $\frac{4}{x^{2} - 1} + \frac{x + 2}{1 - x} = - 1$ ．

查看试题解析
20. 先化简，再求值： $\frac{1}{x + 1} - \frac{3 - x}{x^{2} - 6 x + 9} \div \frac{x^{2} + x}{x - 3}$ ，其中x= $- \frac{3}{2}$ ．

查看试题解析
21. 如图，在△ABC中，AB=AC，∠CAE是△ABC的一个外角．

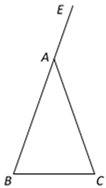(1)、用尺规作图方法，按要求作图：（保留作图痕迹，不写作法和证明）
①作△ABC的高AD；

②作∠CAE的平分线AM；

(2)、判断（1）中的AM与BC的位置关系，并证明你的结论．

查看试题解析
22. 在如图所示的正方形网格中，每个小正方形的边长为 $1 ，$ 格点三角形(顶点是网格线的交点的三角形） $A B C$ 的顶点 $A ， C$ 的坐标分别为 $(- 4 ， 5) ， (- 1 ， 3)$ ．

⑴请在如图所示的网格平面内作出平面直角坐标系；

⑵请作出 $△ A B C$ 关于y轴对称的 $△ A_{1} B_{1} C_{1}$ ；

⑶求 $△ A B C$ 的面积．

查看试题解析
23. 佳佳果品店在批发市场购买某种水果销售，第一次用1200元购进若干千克，并以每千克8元出售，很快售完．由于水果畅销，第二次购买时，每千克的进价比第一次提高了10%，用1452元所购买的数量比第一次多20千克，以每千克9元售出100千克后，因出现高温天气，水果不易保鲜，为减少损失，便降价50%售完剩余的水果．

(1)、求第一次水果的进价是每千克多少元？

(2)、该果品店在这两次销售中，总体上是盈利还是亏损？盈利或亏损了多少元？

查看试题解析
24. 如图，在△ABC中，∠ACB＝90°，CA＝CB ．点E为△ABC外一点，CE＝CA ，且CD平分∠ACB交AE于点D ，且∠CDE＝60°，求∠DCE的度数．

查看试题解析
25. 如图，Rt△ABC中，∠BCA＝90°，AC＝BC ，点D是BC的中点，CE⊥AD于E ， BF∥AC交CE的延长线于点F ．

(1)、求证：△ACD≌△CBF；

(2)、连结DF ，求证：AB垂直平分DF；

(3)、连结AF ，试判断△ACF的形状，并说明理由．

查看试题解析