辽宁省营口市大石桥市2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-05 类型：期末考试

进入出卷网下载

一、单选题

1. 现实世界中，对称现象无处不在，中国的方块字中有些也只有对称性，下列汉字是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
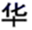2. 下列长度的三条线段，能组成三角形的是（）

A、4，5，9 B、8，8，15 C、5，5，10 D、6，7，14

查看试题解析
3. 下列运算中正确的有（）
① $a^{2} \cdot a^{3} = a^{6}$ ② ${(a^{3})}^{2} = a^{6}$ ③ ${(a b)}^{3} = a^{3} b^{3}$ ④ $a^{5} \div a^{5} = a$

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 如果分式 $\frac{x^{2} - 1}{x + 1}$ 的值为零，那么x应为（）

A、1 B、-1 C、±1 D、0

查看试题解析
5. 已知点A的坐标为 $(2 ， 5)$ ，点B的坐标为 $(2 ， 1)$ ，将线段 $A B$ 沿坐标轴翻折后，若点A的对应点 $A^{'}$ 的坐标为 $(2 ， - 5)$ ，则点B的对应点 $B^{'}$ 的坐标为（）

A、 $(2 ， - 1)$ B、 $(2 ， 2)$ C、 $(- 2 ， 1)$ D、 $(- 2 ， - 1)$

查看试题解析
6. 若 $a + b = 6$ ， $a b = 4$ ，则 $a^{2} + a b + b^{2}$ 的值为（）

A、40 B、36 C、32 D、30

查看试题解析
7. 如图， $A D$ 平分 $∠ B A C$ 交 $B C$ 于点D， $D E ⊥ A B$ 于点E， $D F ⊥ A C$ 于点F．若 $S_{△ A B C} = 8$ ， $D F = 2$ ， $A C = 3$ ，则 $A B$ 的长是（）

A、8 B、7 C、6 D、5

查看试题解析
8. 若一个正n边形的每个内角为144°，则这个正 $n$ 边形的边数为（）

A、8 B、9 C、10 D、11

查看试题解析
9. 如图，在 $△ ABC$ 中， $∠ BAC = 120^{\circ}$ ，点D是BC上一点，BD的垂直平分线交AB于点E，将 $△ ACD$ 沿AD折叠，点C恰好与点E重合，则 $∠ B$ 等于 $($ 　　 $)$

A、 $18^{\circ}$ B、 $20^{\circ}$ C、 $25^{\circ}$ D、 $28^{\circ}$

查看试题解析
10. 如图，D为 $∠ B A C$ 的外角平分线上一点并且满足 $B D = C D$ ，过D作 $D E ⊥ A C$ 于E， $D F ⊥ A B$ 交BA的延长线于F，则下列结论：
① $△ C D E ≅ △ B D F$ ，② $C E = A B + A E$ ，③ $∠ B D C = ∠ B A C$ ，④ $∠ D A F = ∠ C B D$ ，其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若x²+kx﹣15＝（x+3）（x+b），则k＝.

查看试题解析
12. 计算： $2021 \times 2019 - 2020^{2} =$

查看试题解析
13. 如图， $△ A C E ≌ △ D B F$ ， $A E // D F$ ， $A D = 8$ ， $B C = 2$ ，则 $A B =$ ．

查看试题解析
14. 如图，在 $△ A B C$ 与 $△ A D E$ 中， $∠ B A C = ∠ D A E = 90 °$ ， $A B = A C$ ， $A D = A E$ ，点C，D，E在同一条直线上，连接 $B D$ ， $B E$ ，则 $∠ A C E + ∠ D B C =$ ．

查看试题解析
15. 如图，四边形ABCD中，AB=AD，AC=4，∠DAB=∠DCB=90°，则四边形ABCD的面积是．

查看试题解析
16. 如图：已知 $△ A B C$ 是等腰三角形， $∠ B A C = 120 °$ ， $A B = A C = 6$ ，点D是 $B C$ 上的中点，点E是射线 $A D$ 上的一动点，点F是射线 $C A$ 上的一动点，且 $A E = C F$ ，连接 $B F$ 、 $C E$ ，则 $B F + C E$ 的最小值．

查看试题解析

三、解答题

17. 计算：

(1)、 ${(m^{2} n)}^{3} \cdot (- m^{3} n) \div {(- m n)}^{2}$ ；

(2)、 $[{(x + y)}^{2} - (x + y) (x - y)] \div 2 y$ ；

(3)、 $\frac{a^{2} - 6 a + 9}{a^{2} - 4} \cdot \frac{a - 2}{3 - a}$ ．

查看试题解析
18. 分解因式：

(1)、 $- 3 x^{2} + 6 x y - 3 y^{2}$ ；

(2)、 $(a - 4) (a + 1) + 3 a$ ．

查看试题解析
19. 解方程：

(1)、 $\frac{5 x + 2}{x^{2} + x} = \frac{3}{x + 1}$ ；

(2)、 $\frac{x}{x - 1} - 1 = \frac{3}{x^{2} - 1}$ ．

查看试题解析
20. 先化简： $\frac{x^{2} - 4}{x^{2} - 4 x + 4} + \frac{x}{x^{2} - x}$ ÷ $\frac{x - 2}{x - 1}$ 在从﹣1≤x≤3的整数中选取一你喜欢的x的值代入求值．

查看试题解析
21. 如图，在 $Rt △ A B C$ 中， $C M$ 平分 $∠ A C B$ 交 $A B$ 于点M，过点M作 $M N // B C$ 交 $A C$ 于点N，且 $M N$ 平分 $∠ A M C$ ，若 $A N = 1$ ．

(1)、求 $∠ B$ 的度数；

(2)、求 $C N$ 的长．

查看试题解析
22. 某工程限期完成，甲队单独做正好按期完成，乙队单独做则要误期3天．现两队合作2天后，余下的工程再由乙队单独做，也正好如期完成，该工程限期多少天？

查看试题解析
23. 数学课上，老师出示了如下的题目．在等边三角形 $A B C$ 中，点E在边 $A B$ 上，点D在 $C B$ 的延长线上，且 $E D = E C$ ，如图，试确定线段 $A E$ 与 $D B$ 的大小关系，并说明理由．

第一学习小组讨论后，进行了如下解答：

(1)、特殊情况，探索结论：当点E为边 $A B$ 的中点时，如图2，确定线段 $A E$ 与 $D B$ 的大小关系，请你直接写出结论： $A E$ $D B$ （填“ $>$ ”，“ $<$ ”或“ $=$ ”）．

(2)、一般情况，启发解答：当点E为边 $A B$ 上任意一点时，如图1，试确定线段 $A E$ 与 $D B$ 的大小关系，并说明理由．

查看试题解析
24. 如图所示，△ABC中，∠ACB=90°，AC=6cm，BC =8cm.点P从A点出发，沿 $A - C - B$ 路径向终点B运动，点Q从B点出发，沿 $B - C - A$ 路径向终点A运动.点P 和Q分别 $1 c m / s$ 和 $3 c m / s$ 的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过点P和Q作PE⊥l于E，QF⊥l于F.则点P运动多少秒时，△PEC和△CFQ全等？请说明理由.

查看试题解析
25. 如图1所示，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，点D是线段 $C A$ 延长线上一点，且 $A D = A B$ ，点F是线段 $A B$ 上一点，连接 $D F$ ，以 $D F$ 为斜边作等腰 $R t △ D F E$ ，连接 $E A$ ， $E A$ 满是条件 $E A ⊥ A B$ .

(1)、若 $∠ A E F = 20 °$ ， $∠ A D E = 50 °$ ， $B C = 2$ ，求 $A B$ 的长度；

(2)、求证： $A E = A F + B C$ ；

(3)、如图2，点F是线段 $B A$ 延长线上一点，其余条件与题干一致，探究 $A E$ 、 $A F$ 、 $B C$ 之间的数量关系，并证明你的结论.

查看试题解析