辽宁省沈阳市沈河区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-05 类型:期末考试
一、单选题
-
1. 下列各数中,无理数是( )A、0.121221222 B、 C、 D、2. 如图,已知DC‖EG,∠C=40°,∠A=70°,则∠AFE的度数为( )
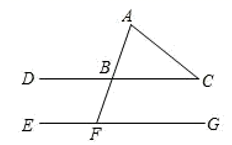 A、140° B、110° C、90° D、30°3. (﹣ )2的平方根是( )A、﹣ B、 C、± D、±4. 下列命题中,是真命题的是( )A、如果a>b,那么a2>b2 B、两直线被第三条直线所截,截得的内错角相等 C、三角形的外角大于三角形的内角 D、对顶角相等5. 下列各组线段 、 、 中不能组成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,6. 若点 在函数 的图象上,则m的值是( )A、 B、 C、 D、7. 如图,小手盖住的点的坐标可能是( ).
A、140° B、110° C、90° D、30°3. (﹣ )2的平方根是( )A、﹣ B、 C、± D、±4. 下列命题中,是真命题的是( )A、如果a>b,那么a2>b2 B、两直线被第三条直线所截,截得的内错角相等 C、三角形的外角大于三角形的内角 D、对顶角相等5. 下列各组线段 、 、 中不能组成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,6. 若点 在函数 的图象上,则m的值是( )A、 B、 C、 D、7. 如图,小手盖住的点的坐标可能是( ).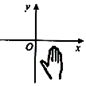 A、(5,2) B、(-6,3) C、(-4,6) D、(3,-4)8. 20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人,根据题意,列方程组正确的是( )A、 B、 C、 D、9. 李明参加某单位招聘测试,他的笔试、面试、技能操作得分分别为86分、80分、90分,若依次按照 的比例确定成绩,则李明的成绩是( )A、256分 B、86分 C、86.2分 D、88分10. 已知函数y=kx+b的图象如图所示,则y=2kx+b的图象可能是( )
A、(5,2) B、(-6,3) C、(-4,6) D、(3,-4)8. 20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人,根据题意,列方程组正确的是( )A、 B、 C、 D、9. 李明参加某单位招聘测试,他的笔试、面试、技能操作得分分别为86分、80分、90分,若依次按照 的比例确定成绩,则李明的成绩是( )A、256分 B、86分 C、86.2分 D、88分10. 已知函数y=kx+b的图象如图所示,则y=2kx+b的图象可能是( ) A、
A、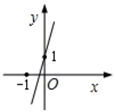 B、
B、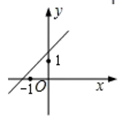 C、
C、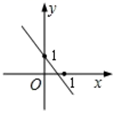 D、
D、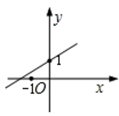
二、填空题
-
11. 8的立方根是 .12. 如图,直线 与直线 相交于点 ,则方程组 的解是 .
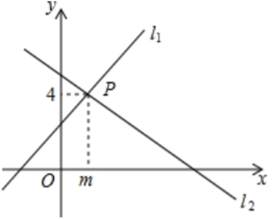 13. 估计 与0.5的大小关系是: 0.5.(填“>”、“=”、“<”)14. 如果将一副三角板按如图方式叠放,那么∠1的大小为 .
13. 估计 与0.5的大小关系是: 0.5.(填“>”、“=”、“<”)14. 如果将一副三角板按如图方式叠放,那么∠1的大小为 . 15. 已知某汽车装满油后油箱中的剩余油量y(升)与汽车的行驶路程x(千米)之间具有一次函数关系(如图所示).为了行驶安全考虑,邮箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶千米,就应该停车加油.
15. 已知某汽车装满油后油箱中的剩余油量y(升)与汽车的行驶路程x(千米)之间具有一次函数关系(如图所示).为了行驶安全考虑,邮箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶千米,就应该停车加油.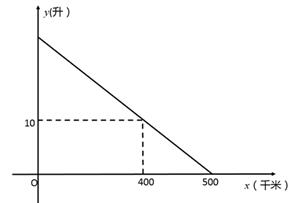 16. 如图,点A坐标为(0,4),点B坐标为(4,2).直线BC垂直于y轴于点C.点D在直线BC上,点B关于直线AD的对称点在y轴上,则点D的坐标为 .
16. 如图,点A坐标为(0,4),点B坐标为(4,2).直线BC垂直于y轴于点C.点D在直线BC上,点B关于直线AD的对称点在y轴上,则点D的坐标为 . 17. 我市某中学举行“校园好声音”歌手大赛,甲、乙两班根据初赛成绩各选出5名选手组成甲班代表队和乙班代表队参加学校决赛,两个队各选出的5名选手的决赛成绩(满分100)如图所示:
17. 我市某中学举行“校园好声音”歌手大赛,甲、乙两班根据初赛成绩各选出5名选手组成甲班代表队和乙班代表队参加学校决赛,两个队各选出的5名选手的决赛成绩(满分100)如图所示:根据图示信息,整理分析数据如表:
平均数(分)
中位数(分)
众数(分)
方差
甲班
a
85
c
70
乙班
85
b
100
160
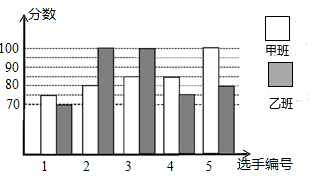 (1)、填空:甲班2号选手的预赛成绩是分,乙班3号选手的预赛成绩是分,班的预赛成绩更平衡,更稳定;(2)、求出表格中a= , b= , c=;(3)、学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的区级比赛,这5人预赛成绩的平均分数为 .
(1)、填空:甲班2号选手的预赛成绩是分,乙班3号选手的预赛成绩是分,班的预赛成绩更平衡,更稳定;(2)、求出表格中a= , b= , c=;(3)、学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的区级比赛,这5人预赛成绩的平均分数为 .三、解答题
-
18. 计算:(1)、 ﹣ +2 ÷ ;(2)、 ﹣ × .19. 解方程组:(1)、 ;(2)、 .20. 已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30°.
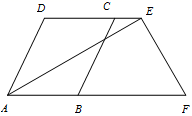 (1)、求证:DC//AB.(2)、求∠AFE的大小21. 在如图所示的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
(1)、求证:DC//AB.(2)、求∠AFE的大小21. 在如图所示的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在正方形网格的格点(网格线的交点)上.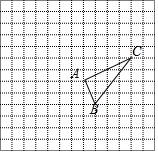
(1)请在如图所示的网格平面内作出平面直角坐标系,使点A坐标为(1,3),点B坐标为(2,1),则C点坐标为 ▲ ;
(2)画出△ABC关于y轴对称的图形为△A1B1C1 , 并写出点B1的坐标为 ▲ ;写出△A1B1C1的面积为 ▲ ;
(3)在y轴上画出P点,使得PA+PC的值最小,最小值为 ▲ .22. 小明的妈妈今天在菜市场买回2斤萝卜、1斤排骨共花了43.8元,而两个月前买同重量的这两样菜只要37元,与两个月前相比,这次萝卜的单价下降了10%,但排骨单价却上涨了20%,求:两个月前买的萝卜和排骨的单价分别为多少元?23. 如图1,甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时.并以各自的速度匀速行驶,甲车到达C地后因有事按原路原速返回A地,乙车从B地直达A地,两车同时到达A地.甲、乙两车距A地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图2,结合图象信息解答下列问题: (1)、乙车的速度是千米/时,乙车行驶的时间t=小时;(2)、求甲车从C地按原路原速返回A地的过程中,甲车距A地的路程y与它出发的时间x的函数关系式;(3)、直接写出甲车出发多长时间两车相距110千米 .24. 如图,在Rt ABC中,∠A=90°,AB=AC,BC=10,点D是直线AC上一动点,∠BDE=90°,DB=DE(DE在BD的左侧).
(1)、乙车的速度是千米/时,乙车行驶的时间t=小时;(2)、求甲车从C地按原路原速返回A地的过程中,甲车距A地的路程y与它出发的时间x的函数关系式;(3)、直接写出甲车出发多长时间两车相距110千米 .24. 如图,在Rt ABC中,∠A=90°,AB=AC,BC=10,点D是直线AC上一动点,∠BDE=90°,DB=DE(DE在BD的左侧).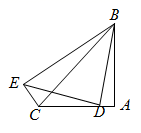 (1)、直接写出AB长为;(2)、若点D在线段AC上,AD= ,求EC长;(3)、当BE=2 时,直接写出CD长为 .25. 如图1,直线y= x和直线y=﹣ x+5相交于点A,直线y=﹣ x+5与x轴交于点C,点P在线段AC上,PD⊥x轴于点D,交直线y= x于点Q.
(1)、直接写出AB长为;(2)、若点D在线段AC上,AD= ,求EC长;(3)、当BE=2 时,直接写出CD长为 .25. 如图1,直线y= x和直线y=﹣ x+5相交于点A,直线y=﹣ x+5与x轴交于点C,点P在线段AC上,PD⊥x轴于点D,交直线y= x于点Q.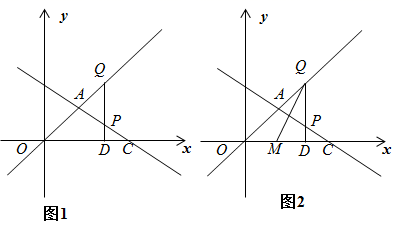 (1)、点A的坐标为;(2)、当QP=OA时,求Q点的坐标及△APQ的面积;(3)、如图2,在(2)的条件下,∠OQP平分线交x轴于点M.
(1)、点A的坐标为;(2)、当QP=OA时,求Q点的坐标及△APQ的面积;(3)、如图2,在(2)的条件下,∠OQP平分线交x轴于点M.①直接写出点M的坐标;
②点N在直线y= x的上方,当 OQN和 OQM全等时直接写出N点坐标 .