辽宁省沈阳市皇姑区2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-05 类型：期末考试

进入出卷网下载

一、单选题

1. 16的算术平方根是（）

A、8 B、-8 C、4 D、 $\pm 4$

查看试题解析
2. 一个直角三角形的两条直角边分别是5和12，则斜边是（　　）

A、13 B、12 C、15 D、10

查看试题解析
3. 下列计算：①（ $\sqrt{2}$ ）²＝2；② $\sqrt{{(- 2)}^{2}}$ ＝2；③ $(- 2 \sqrt{2})$ ²＝12；④ $(\sqrt{2} + \sqrt{3}) (\sqrt{2} - \sqrt{3}) = - 1$ ，结果正确的个数为（）个

A、1 B、2 C、3 D、4

查看试题解析
4. 在平面直角坐标系中，点 $(0 ， - 2)$ 在（）．

A、 $x$ 轴正半轴上 B、 $x$ 轴负半轴上 C、 $y$ 轴正半轴上 D、 $y$ 轴负半轴上

查看试题解析
5. 已知 ${\begin{array}{l} x = 2 \\ y = - 5 \end{array}$ 是关于x、y的二元一次方程3x-ay=7的一个解，则a的值为（）

A、5 B、 $\frac{1}{5}$ C、- $\frac{1}{5}$ D、-5

查看试题解析
6. 某校举办“喜迎建党100周年”校园朗诵大赛，小丽同学根据比赛中七位评委所给的某位参赛选手的分数，制作了一个表格，如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（）

中位数

众数

平均数

方差

9.3

9.4

9.2

9.5

A、中位数 B、众数 C、平均数 D、方差

查看试题解析
7. 如图，已知直线m∥n，将一块含45°角的直角三角板ABC，按如图所示方式放置，其中斜边AC与直线m交于点D．若∠2＝25°，则∠1的度数为（）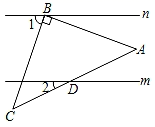

A、25° B、45° C、70° D、75°

查看试题解析
8. 一次函数y＝kx+b与y＝x+2的图象相交于如图点P（m ， 4），则关于x ， y的二元一次方程组 ${\begin{array}{l} y = k x + b \\ y = x + 2 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 3 \\ y = 4 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 4 \end{array}$ C、 ${\begin{array}{l} x = 2.4 \\ y = 4 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 4 \end{array}$

查看试题解析
9. 如图，矩形 $A B C D$ 中， $A B = 3$ ， $A D = 1$ ， $A B$ 在数轴上，若以点A为圆心，对角线 $A C$ 的长为半径作弧交数轴于点M ，则点M表示的数为（）

A、2 B、 $\sqrt{5} - 1$ C、 $\sqrt{10} - 1$ D、 $\sqrt{5}$

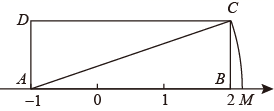查看试题解析
10. 为了研究吸烟是否对肺癌有影响，某肿瘤研究所随机地调查了10000人，并进行统计分析.结果显示：在吸烟者中患肺癌的比例是2.5%，在不吸烟者中患肺癌的比例是0.5%，吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人.如果设这10000人中，吸烟者患肺癌的人数为x，不吸烟者患肺癌的人数为y，根据题意，下面列出的方程组正确的是（）

A、 ${\begin{cases} x - y = 22 \\ x \times 2.5 % + y \times 0.5 % = 10000 \end{cases}$ B、 ${\begin{cases} x - y = 22 \\ \frac{x}{2.5 %} + \frac{y}{0.5 %} = 10000 \end{cases}$ C、 ${\begin{cases} x + y = 10000 \\ x \times 2.5 % - y \times 0.5 % = 22 \end{cases}$ D、 ${\begin{cases} x + y = 10000 \\ \frac{x}{2.5 %} - \frac{y}{0.5 %} = 22 \end{cases}$

查看试题解析

二、填空题

11. 在 $\sqrt{2}$ ， $\frac{22}{7}$ ， $- \sqrt{\frac{25}{4}}$ ，3.14，2.12这些数中，无理数是．

查看试题解析
12. 在平面直角坐标系中，点A（﹣3，6）到y轴的距离为.

查看试题解析
13. 已知 ${\begin{array}{l} 4 x + y = 5 \\ 3 x + 2 y = 4 \end{array}$ ，则x﹣y＝．

查看试题解析
14. 比较大小关系 $\frac{\sqrt{5} + 1}{2}$ 1.5（填“ $>$ ”、“ $=$ ”或“ $<$ ”）

查看试题解析
15. 对于实数 $m ， n$ ，定义运算 $m * n = {(m + 2)}^{2} - 2 n$ .若 $2 * a = 4 * (- 3)$ ，则 $a =$ .

查看试题解析
16. 如图，在一张长为18cm、宽为16cm的长方形纸片上，现要剪一个腰长为10cm的等腰三角形（要求：等腰三角形的一个顶点与长方形的一个顶点重合，其余两个顶点在长方形的边上），则剪下的等腰三角形的面积是．

查看试题解析

三、解答题

17. 计算： $\sqrt{81} + \sqrt[3]{- 27} + \sqrt{4} - | \sqrt{3} - 2 |$ ．

查看试题解析
18. 解二元一次方程组： ${\begin{matrix} 3 y + 5 x = 8 \\ 2 y - x = 1 \end{matrix}$ ．

查看试题解析
19. 如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．由图观察易知点A（0，2），B（5，3）、C（﹣2，5）．

(1)、若点A、B、C关于直线l的对称点分别为A₁、B₁、C₁ ，请直接在图中画出△A₁B₁C₁；

(2)、坐标平面内任一点P（a ， b）关于第一、三象限的角平分线l的对称点P′的坐标为．

查看试题解析
20. 2020年是特殊的一年，新年以来我们经历了新型冠状病毒肺炎，举国上下众志成城，共同抗疫.严酷战疫中，我们又一次感受到祖国的强大.口罩也成为人们防护防疫的必备武器.临高县某药店有 $2500$ 枚口罩准备出售.从中随机抽取了一部分口罩，根据它们的价格(单位：元)，绘制出如下的统计图.请根据相关信息，解答下列问题：

(1)、图 $①$ 中m的值为；

(2)、统计的这组数据的平均数为众数为，中位数为

(3)、根据样本数据，估计这 $2500$ 枚口罩中，价格为 $2.0$ 元的约有为枚.

查看试题解析
21. （列二元一次方程组解应用题）
运动会结束后，八年级一班准备购买一批明信片奖励积极参与的同学，计划用班费180元购买A、B两种明信片共20盒，已知A种明信片每盒12元，B种明信片每盒8元，求应购买A、B两种明信片各几盒．

查看试题解析
22. 小华和小峰是两名自行车爱好者，小华的骑行速度比小峰快．两人准备在周长为250米的赛道上进行一场比赛．若小华在小峰出发15秒之后再出发，图中l₁、l₂分别表示两人骑行路程与时间的关系．

(1)、小峰的速度为米/秒．

(2)、小华为了能和小峰同时到达终点，设计了两个方案，方案一：加快骑行速度；方案二：比预定时间提前出发．
①图（填“A”或“B”）代表方案一；

②若采用方案二，使小华与小峰同时到达终点，求小华比小峰晚出发多少秒？

查看试题解析
23. 已知：AB∥CD ，点E在直线AB上，点F在直线CD上．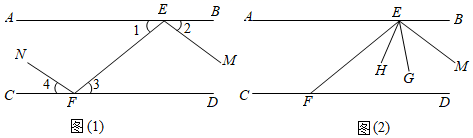

(1)、如图（1），∠1＝∠2，∠3＝∠4.证EM∥FN；

(2)、如图（2），EG平分∠MEF ， EH平分∠AEM ，直接写出∠GEH与∠EFD的数量关系．

查看试题解析
24. 如图在平面直角坐标系中，已知点A（﹣6，0），点B（0，6）分别在坐标轴上，连接AB ．

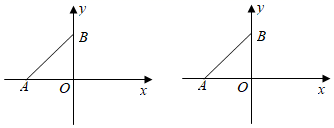(1)、求∠ABO的度数；

(2)、动点P从原点O出发，沿x轴向右每秒1个单位长度的速度运动，运动时间为t秒，当△ABP为等腰三角形时，直接写出t的值（点P不与点O重合）；

(3)、动点P从原点O出发，沿x轴向左每秒1个单位长度的速度运动，运动时间为t秒，当∠PBO＝ $\frac{1}{2}$ ∠PAB时，直接写出t的值．

查看试题解析
25. 如图在平面直角坐标系中，直线l₁：y＝﹣x＋4与y轴交于点A ，与直线l₂：y＝kx＋b交于点C（6，n），直线l₂：与y轴交于点B（0，﹣4）．

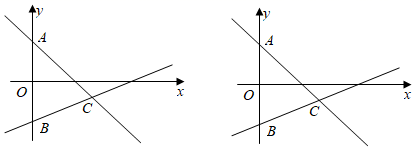(1)、求直线l₂的函数表达式；

(2)、点D（m ， 0）是x轴上的一个动点，过点D作x轴的垂线，交l₁于点M ，交l₂于点N ，当S_△AMB＝2S_△CMB时，请直接写出线段MN的长．

查看试题解析

中位数	众数	平均数	方差
9.3	9.4	9.2	9.5