辽宁省沈阳市大东区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-05 类型:期末考试
一、单选题
-
1. 下列长度的三条线段能组成直角三角形的是( )A、5,11,12 B、3,4,5 C、4,6,8 D、6,12,132. 下列运算正确的是( )A、 B、 C、 D、3. 在平面直角坐标系中,点 位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列函数中,是正比例函数的是( )A、 B、 C、 D、5. 若 是二元一次方程 的解,则m为( )A、7 B、6 C、 D、06. 已知一组数据5,8,8,9,10,以下说法错误的是( )A、平均数是8 B、众数是8 C、中位数是8 D、方差是87. 如图,将一副直角三角板,按如图所示叠放在一起,则图中 的度数是( )
 A、75° B、100° C、105° D、115°8. 如图,在 中, 的垂直平分线交 于点D, 平分 ,若 ,则 的度数为( )
A、75° B、100° C、105° D、115°8. 如图,在 中, 的垂直平分线交 于点D, 平分 ,若 ,则 的度数为( )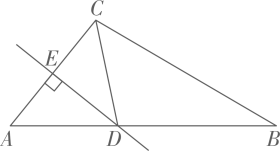 A、 B、 C、 D、9. 估计 的值应在( )A、7和8之间 B、8和9之间 C、9和10之间 D、10和11之间10. 小亮从家O , 步行到公交站台B , 等公交车去学校C , 图中的折线表示小亮的行程s(千米)与所花时间t(分)之间的函数关系.下列说法错误的是( )
A、 B、 C、 D、9. 估计 的值应在( )A、7和8之间 B、8和9之间 C、9和10之间 D、10和11之间10. 小亮从家O , 步行到公交站台B , 等公交车去学校C , 图中的折线表示小亮的行程s(千米)与所花时间t(分)之间的函数关系.下列说法错误的是( ) A、他家到公交车站台为1千米 B、他等公交车的时间为6分钟 C、他步行的速度100米/分钟 D、公交车的速度是350米/分钟
A、他家到公交车站台为1千米 B、他等公交车的时间为6分钟 C、他步行的速度100米/分钟 D、公交车的速度是350米/分钟二、填空题
-
11. 实数0, , ,3.141441444中无理数是 .12. 若一组数据1,3,x,5,4,6的平均数是4,则这组数据的中位数是.13. 如图,一根旗杆在离地面5 m处断裂,旗杆顶部落在离旗杆底部12 m处,旗杆断裂之前的高为.
 14. 已知一次函数 和 ( )的图象相交于点 ,则二元一次方程组 的解是 .15. 如图,把 沿线段 折叠,使点A落在线段 上的点F处, ,若 ,则 度.
14. 已知一次函数 和 ( )的图象相交于点 ,则二元一次方程组 的解是 .15. 如图,把 沿线段 折叠,使点A落在线段 上的点F处, ,若 ,则 度. 16. 如图,已知一次函数 的图象与x轴、一次函数 的图象分别交于点C,D,点D的坐标为 .若在x轴上存在点E,使得以点C,D,E为顶点的三角形是直角三角形,请写出点E的坐标 .
16. 如图,已知一次函数 的图象与x轴、一次函数 的图象分别交于点C,D,点D的坐标为 .若在x轴上存在点E,使得以点C,D,E为顶点的三角形是直角三角形,请写出点E的坐标 .
三、解答题
-
17.(1)、解方程组 ;(2)、计算: .18. 如图,在正方形网格中每个小正方形的边长为1,小正方形的顶点称为格点,在正方形网格中分别画出下列图形:
 (1)、在图(1)网格中画出长为 的线段AB.(2)、在图(2)网格中画出一个腰长为 ,面积为3的等腰19. 如图,在平面直角坐标系中,已知 , , .
(1)、在图(1)网格中画出长为 的线段AB.(2)、在图(2)网格中画出一个腰长为 ,面积为3的等腰19. 如图,在平面直角坐标系中,已知 , , . (1)、请在平面直角坐标系中描出A,B,C三点,再连接 , , ,并求 的面积;(2)、连接 , ,请直接写出 面积的值.20. 某公司想招聘一名新职员,对甲、乙、丙三名应试者进行了面试、笔试和才艺三个方面的量化考核,他们的各项得分(百分制,单位:分)如表所示:
(1)、请在平面直角坐标系中描出A,B,C三点,再连接 , , ,并求 的面积;(2)、连接 , ,请直接写出 面积的值.20. 某公司想招聘一名新职员,对甲、乙、丙三名应试者进行了面试、笔试和才艺三个方面的量化考核,他们的各项得分(百分制,单位:分)如表所示:应试者
面试成绩
笔试成绩
才艺
甲
86
79
90
乙
84
81
75
丙
80
90
73
(1)、请通过计算三项得分的平均分,从低到高确定应聘者的排名顺序;(2)、公司规定:面试、笔试、才艺得分分别不得低于80分、80分、70分,并按照50%、40%、10%的比例计入个人总分,请你确定谁会被录用?并说明理由.
21. 如图,在 中, , ,D为 延长线上一点,点E在 上,且 . (1)、求证: ;(2)、若过B点作 ,且 ,求 度数.22. 甲、乙两种商品原来的单价和为100元.因市场变化,甲商品提价40%,乙商品降价10%,两种商品的单价和比原来提高了20%.问甲、乙两种商品原来的单价各是多少元?23. 如图,在平面直角坐标系中, 的顶点O为坐标原点, ,边 在x轴的正半轴上,边 在y轴的正半轴上,点A的坐标为 ,且 ,动点C从点B出发沿着射线 的方向以每秒1个单位长度的速度匀速运动,动点D从点A出发沿着射线 的方向以每秒2个单位长度的速度匀速运动,已知点C和点D同时出发,设它们的运动时间为t秒( ).
(1)、求证: ;(2)、若过B点作 ,且 ,求 度数.22. 甲、乙两种商品原来的单价和为100元.因市场变化,甲商品提价40%,乙商品降价10%,两种商品的单价和比原来提高了20%.问甲、乙两种商品原来的单价各是多少元?23. 如图,在平面直角坐标系中, 的顶点O为坐标原点, ,边 在x轴的正半轴上,边 在y轴的正半轴上,点A的坐标为 ,且 ,动点C从点B出发沿着射线 的方向以每秒1个单位长度的速度匀速运动,动点D从点A出发沿着射线 的方向以每秒2个单位长度的速度匀速运动,已知点C和点D同时出发,设它们的运动时间为t秒( ). (1)、请直接写出线段 的长和点B的坐标;(2)、当 时,连结 ,求点C的坐标和 的长:(3)、当 为等腰三角形时,请直接写出t的值.24. 在 中, , ,且 .
(1)、请直接写出线段 的长和点B的坐标;(2)、当 时,连结 ,求点C的坐标和 的长:(3)、当 为等腰三角形时,请直接写出t的值.24. 在 中, , ,且 . (1)、如图1,点D,E分别在边 , 上,连接 .直接写出 的值 , 的值;(2)、现将 如图2放置,连接 , , ,求证: ;(3)、现将 如图3放置,使C,A,E三点共线,延长 交 于点F,求证: 垂直平分 .25. 如图1,在平面直角坐标系 中,直线 分别与x轴,y轴交于A,B两点,已知A点坐标 ,点C在直线 上,且点C的纵坐标为3,点D是x轴正半轴上的一个动点,连结 ,以 为直角边在右侧作等腰 ,且 .
(1)、如图1,点D,E分别在边 , 上,连接 .直接写出 的值 , 的值;(2)、现将 如图2放置,连接 , , ,求证: ;(3)、现将 如图3放置,使C,A,E三点共线,延长 交 于点F,求证: 垂直平分 .25. 如图1,在平面直角坐标系 中,直线 分别与x轴,y轴交于A,B两点,已知A点坐标 ,点C在直线 上,且点C的纵坐标为3,点D是x轴正半轴上的一个动点,连结 ,以 为直角边在右侧作等腰 ,且 .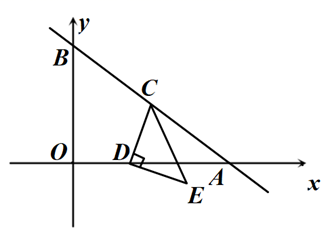
 (1)、求直线 的函数表达式和C点坐标:(2)、设点D的横坐标为t,求点E的坐标(用含t的代数式表示);(3)、如图2,连结 , ,请直接写出当 周长最小时,点E的坐标.
(1)、求直线 的函数表达式和C点坐标:(2)、设点D的横坐标为t,求点E的坐标(用含t的代数式表示);(3)、如图2,连结 , ,请直接写出当 周长最小时,点E的坐标.