辽宁省盘锦市大洼区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-05 类型:期末考试
一、单选题
-
1. 下列四个交通标志图中,为轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、 · = B、m6÷m2= m3(m≠0) C、 D、(2m+1)(m-1)=2m2-m-13. 用科学记数法表示数0.00002正确的是( )A、0.2× B、2× C、2× D、2×4. 点A(-3,3)关于x轴对称的点A1的坐标是( )A、(3,0) B、(3,-3) C、(3,3) D、(-3,-3)5. 等腰三角形的顶角是 ,则它的底角是( )A、 B、 C、 或 D、 或6. 一个多边形的内角和等于1080°,则这个多边形的每个外角都等于( )A、30° B、45° C、60° D、90°7. 某市道路改造中,需要铺设一条长为1200米的管道,为了尽量减少施工对交通造成的影响,实际施工时,工作效率比原计划提高了25%,结果提前了8天完成任务.设原计划每天铺设管道x米,根据题意,则下列方程正确的是( )A、 B、 C、 D、8. 如图,纸片△ABC中,AB=AC,∠A=40°,将纸片对折,使点A与点B重合,折痕为DE,连结BE.则∠EBC 的度数为( )
2. 下列运算正确的是( )A、 · = B、m6÷m2= m3(m≠0) C、 D、(2m+1)(m-1)=2m2-m-13. 用科学记数法表示数0.00002正确的是( )A、0.2× B、2× C、2× D、2×4. 点A(-3,3)关于x轴对称的点A1的坐标是( )A、(3,0) B、(3,-3) C、(3,3) D、(-3,-3)5. 等腰三角形的顶角是 ,则它的底角是( )A、 B、 C、 或 D、 或6. 一个多边形的内角和等于1080°,则这个多边形的每个外角都等于( )A、30° B、45° C、60° D、90°7. 某市道路改造中,需要铺设一条长为1200米的管道,为了尽量减少施工对交通造成的影响,实际施工时,工作效率比原计划提高了25%,结果提前了8天完成任务.设原计划每天铺设管道x米,根据题意,则下列方程正确的是( )A、 B、 C、 D、8. 如图,纸片△ABC中,AB=AC,∠A=40°,将纸片对折,使点A与点B重合,折痕为DE,连结BE.则∠EBC 的度数为( )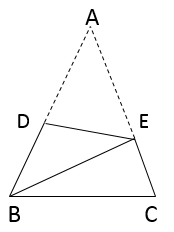 A、30° B、40° C、60° D、80°9. 如图,点B的坐标为(4,4),作BA⊥x轴,BC⊥y轴,垂足分别为A、C,点D为线段OA的中点,点P从点A出发,在线段AB、BC上沿A→B→C运动,当OP=CD时,点P的坐标为( )
A、30° B、40° C、60° D、80°9. 如图,点B的坐标为(4,4),作BA⊥x轴,BC⊥y轴,垂足分别为A、C,点D为线段OA的中点,点P从点A出发,在线段AB、BC上沿A→B→C运动,当OP=CD时,点P的坐标为( ) A、(4,1) B、(4, 2) C、(2,2) D、(4, 2)或(2,4)
A、(4,1) B、(4, 2) C、(2,2) D、(4, 2)或(2,4)二、多选题
-
10. 如图, 那么添加下列一个条件后,无法判定 的是( )
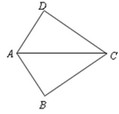
A、 B、 C、 D、三、填空题
-
11. 计算: .12. 计算:(7x2y3﹣14x3y2z)÷7x2y2= .13. 使分式 有意义的x的取值范围是.14. 分解因式: =.15. 已知等腰三角形的两条边长分别等于3和 7,则它的周长等于 .16. 计算: + + + +…+ + = .
四、解答题
-
17. 如图,要在燃气管道 上修建一个泵站,分别向A、B两镇供气,请你利用尺规作图帮助确定泵站P修在什么地方,可使所用的输气管线最短?(保留作图痕迹,不写作法)
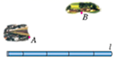 18. 如图,在平面直角坐标系 中, , , .
18. 如图,在平面直角坐标系 中, , , .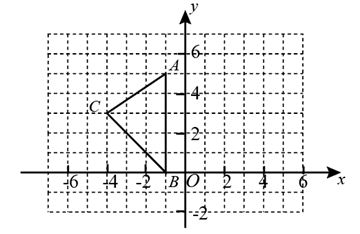 (1)、在图中作出 关于 轴的对称图形 ;(2)、若以线段AB为一边作格点△ABD,使所作的△ABD 与△ABC全等,则所有满足条件的点D的坐标是 .19. 计算:20. 先化简,再求值: ,其中x= -1.21. 解分式方程:22. 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队共同工作了半个月,总工程全部完成.哪个队的施工速度快?23. 一台收割机的工作效率相当于一个农民工作效率的150倍,用这台机器收割10公顷小麦比100个农民人工收割这些小麦要少用1小时.这台收割机每小时收割多少公顷小麦?24. 如图,点D、E在△ABC的边BC上,AB=AC,AD=AE.请你按要求用两种方法证明BD=CD.
(1)、在图中作出 关于 轴的对称图形 ;(2)、若以线段AB为一边作格点△ABD,使所作的△ABD 与△ABC全等,则所有满足条件的点D的坐标是 .19. 计算:20. 先化简,再求值: ,其中x= -1.21. 解分式方程:22. 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队共同工作了半个月,总工程全部完成.哪个队的施工速度快?23. 一台收割机的工作效率相当于一个农民工作效率的150倍,用这台机器收割10公顷小麦比100个农民人工收割这些小麦要少用1小时.这台收割机每小时收割多少公顷小麦?24. 如图,点D、E在△ABC的边BC上,AB=AC,AD=AE.请你按要求用两种方法证明BD=CD.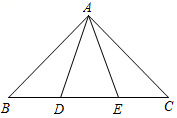 (1)、利用等腰三角形“三线合一”的性质证明:BD=CD;(2)、通过证明三角形全等证明:BD=CD.25. 如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)、利用等腰三角形“三线合一”的性质证明:BD=CD;(2)、通过证明三角形全等证明:BD=CD.25. 如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.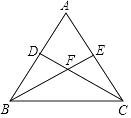 (1)、判断∠ABE与∠ACD的数量关系,并说明理由;(2)、求证:过点A、F的直线垂直平分线段BC.26. 在四边形ABCD中,∠B+∠D=180°,对角线AC平分∠BAD .
(1)、判断∠ABE与∠ACD的数量关系,并说明理由;(2)、求证:过点A、F的直线垂直平分线段BC.26. 在四边形ABCD中,∠B+∠D=180°,对角线AC平分∠BAD . (1)、如图1,若∠B=90°,则线段AB = , D C=;(2)、如图1,若∠DAB=120°,且∠B=90°.试探究边AD、AB与对角线AC的数量关系并说明理由.(3)、如图2,若将(2)中的条件“∠B=90°”去掉,(2)中的结论是否成立?请说明理由.27. 如图,△ABC和△DEF都是等边三角形,点E在AC边上,点D在直线BC上,连结CF.
(1)、如图1,若∠B=90°,则线段AB = , D C=;(2)、如图1,若∠DAB=120°,且∠B=90°.试探究边AD、AB与对角线AC的数量关系并说明理由.(3)、如图2,若将(2)中的条件“∠B=90°”去掉,(2)中的结论是否成立?请说明理由.27. 如图,△ABC和△DEF都是等边三角形,点E在AC边上,点D在直线BC上,连结CF. (1)、如图1,当点D在BC的延长线上时,延长AC到M,使CM=CD,连结MD,
(1)、如图1,当点D在BC的延长线上时,延长AC到M,使CM=CD,连结MD,①判断△CMD的形状,并说明理由;
②求证:∠ACF=60°;
(2)、如图2,当点D在BC边上时,(1)②中的结论是否仍然成立?请说明理由;(3)、当点D在CB的延长线上,点F在BC下方时,∠ACF等于多少度?请在图3中补全图形,做出辅助线,直接写出结论.(不用说明理由)
-