辽宁省葫芦岛市绥中县2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-05 类型：期末考试

进入出卷网下载

一、单选题

1. 若代数式 $\frac{2}{x - 3}$ 有意义，则实数x的取值范围是（）

A、x=0 B、x=3 C、x≠0 D、x≠3

查看试题解析
2. 下列运算，正确的是（　　）

A、a²•a＝a² B、a+a＝a² C、a⁶÷a³＝a² D、（a³）²＝a⁶

查看试题解析
3. 已知点P（a ， 3）、Q（﹣2，b）关于y轴对称，则 $\frac{a + b}{a - b}$ 的值是（）

A、 $- \frac{1}{5}$ B、 $\frac{1}{5}$ C、﹣5 D、5

查看试题解析
4. 如果x²+2ax+9是一个完全平方式，则a的值是（）

A、3 B、﹣3 C、3或﹣3 D、9或﹣9

查看试题解析
5. 已知 $x y = 3$ ， $x - y = - 2$ ，则代数式 $x^{2} y - x y^{2}$ 的值是（）

A、6 B、﹣1 C、﹣5 D、﹣6

查看试题解析
6. 如图，△ABC的一角被墨水污了，但小明很快就画出跟原来一样的图形，他所用定理是（）

A、SAS B、SSS C、ASA D、HL

查看试题解析
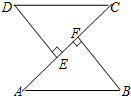
7. 如图，足球图片中的一块黑色皮块的内角和是（　　）

A、720° B、540° C、360° D、180°

查看试题解析
8. 如图，点B、F、C、E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（）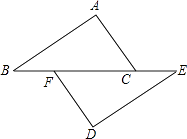

A、AB=DE B、AC=DF C、∠A=∠D D、BF=EC

查看试题解析
9. 如图，折叠直角三角形纸片的直角，使点C落在AB上的点E处，已知BC=24，∠B=30°，则DE的长是（）

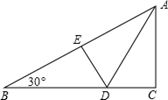A、12 B、10 C、8 D、6

查看试题解析
10. 为了践行“绿色生活”的理念，甲、乙两人每天骑自行车出行，甲匀速骑行30公里的时间与乙匀速骑行25公里的时间相同，已知甲每小时比乙多骑行2公里，设甲每小时骑行x公里，根据题意列出的方程正确的是（）

A、 $\frac{30}{x + 2}$ = $\frac{25}{x}$ B、 $\frac{30}{x}$ = $\frac{25}{x + 2}$ C、 $\frac{30}{x}$ = $\frac{25}{x - 2}$ D、 $\frac{30}{x - 2}$ = $\frac{25}{x}$

查看试题解析

二、填空题

11. （﹣x﹣2y）（﹣x+2y）＝.

查看试题解析
12. 若分式 $\frac{x^{2} - 1}{x - 1}$ 的值为0，则x的值为.

查看试题解析
13. 下列长度的三条线段：①5、6、12；②4、4、10；③4、6、10；④3、4、5．能组成三角形的是．（填序号即可）

查看试题解析
14. 化简 $\frac{a^{2}}{a - b} - \frac{b^{2}}{a - b}$ 的结果是．

查看试题解析
15. 若等腰三角形的一个外角是110°，则其底角为．

查看试题解析
16. 关于x的方程 $\frac{2}{x - 3} + \frac{x + m}{3 - x} = 2$ 有增根，则m的值为

查看试题解析
17. 如图，在△ABC中，DE是BC的垂直平分线，垂足为E，交AC于点D，若AB=6，AC=9，则△ABD的周长是.

查看试题解析
18. 如图，∠C=90°，AD平分∠BAC交BC于点D ，若BC=5cm ， BD=3cm ，则D到AB的距离为．

查看试题解析
19. 如图， $∠ 1 = ∠ 2$ ，要使 $△ A B E ≌ △ A C E$ ，还需添加一个条件是：.（填上你认为适当的一个条件即可）

查看试题解析
20. 如图，4个全等的长方形组成如图所示的图形，其中长方形的边长分别为a和b ，且a＞b ，求出阴影部分的面积为．

查看试题解析

三、解答题

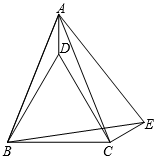
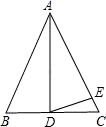
21. 因式分解：

(1)、4xy²﹣4x²y﹣y³；

(2)、9a²（x﹣y）+4b²（y﹣x）．

查看试题解析
22. 解下列方程：

(1)、 $\frac{x}{2 x - 1} + \frac{5}{1 - 2 x} = 2$ ；

(2)、 $\frac{x}{x - 2} - 1 = \frac{8}{x^{2} - 4}$ .

查看试题解析
23. 计算与求值：

(1)、计算： $\frac{a^{2} - b^{2}}{a^{2} + a b}$ ÷（a﹣ $\frac{2 a b - b^{2}}{a}$ ）．

(2)、先化简再求值： $[{(3 x + y)}^{2} - (3 x - y) (3 x + y) - 2 y^{2}] \div 2 x^{2} y^{2}$ ，其中x＝6，y＝﹣ $\frac{1}{2}$ ．

查看试题解析
24. 如图，在△ABC中，AB＝AC，AD⊥BC，∠BAD＝28°，且AD＝AE，求∠EDC的度数．

查看试题解析
25. 如图，在边长为1个单位长度的小正方形组成的12×12网格中，给出了四边形ABCD的两条边AB与BC ，且四边形ABCD是一个轴对称图形，其对称轴为直线AC ．

(1)、在图中标出点D ，并画出该四边形的另两条边；

(2)、将四边形ABCD向下平移5个单位，画出平移后得到的四边形A₁B₁C₁D₁ ，并在对称轴AC上找出一点P ，使PD+PD₁的值最小．

查看试题解析
26. 如图，在Rt△ABC中，∠C＝90°，∠A＝30°．

(1)、尺规作图：作∠B的平分线BD交AC于点D；（不写作法，保留作图痕迹）

(2)、若DC＝2，求AC的长．

查看试题解析
27. 如图，AB=CD，DE⊥AC，BF⊥AC，E，F是垂足，AE=CF，求证：AB∥CD．

查看试题解析
28. 班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动，基地离学校有90公里，队伍8：00从学校出发．苏老师因有事情，8：30从学校自驾小车以大巴1.5倍的速度追赶，追上大巴后继续前行，结果比队伍提前15分钟到达基地．问：大巴与小车的平均速度各是多少？

查看试题解析
29. 如图，已知，在△ABC中，AB＝AC，分别以AB、BC为边作等边△ABE和等边△BCD，连结CE、AD．

(1)、求证：∠ACD＝∠ABD；

(2)、判断DC与CE的位置关系，并加以证明；

查看试题解析