辽宁省葫芦岛市建昌县2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个图形分别是不可回收垃圾、可回收垃圾、有害垃圾、其它垃圾的标志，这四个标志中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若分式 $\frac{1}{a + 3}$ 有意义，则a的取值范围是（）

A、 $a = 0$ B、 $a \neq 0$ C、 $a = - 3$ D、 $a \neq - 3$

查看试题解析
3. 下列计算正确的是（）

A、 $a^{2}$ · $a^{5} = a^{10}$ B、 ${(a^{3})}^{4} = a^{7}$ C、 ${(- a^{2})}^{3} = - a^{6}$ D、 ${(- 3 a^{2})}^{0} = 1$

查看试题解析
4. 已知三角形两边的长分别是4和7，则此三角形第三边的长可能是（）

A、12 B、10 C、11 D、3

查看试题解析
5. 计算2x³÷x²的结果是（）

A、x B、 $2 x$ C、 $2 x^{5}$ D、 $2 x^{6}$

查看试题解析
6. 如果把 $\frac{5 x}{x + y}$ 中的x与y都扩大为原来的10倍，那么这个代数式的值（）

A、扩大为原来的10倍 B、扩大为原来的5倍 C、缩小为原来的 $\frac{1}{2}$ D、不变

查看试题解析
7. 如图，点D是△ABC边BC延长线上的点，∠ACD＝105°，∠A＝70°，则∠B等于（）

A、35° B、40° C、45° D、50°

查看试题解析
8. 下列各式是最简分式的是（）

A、 $\frac{3}{12 x}$ B、 $\frac{x^{2} - y^{2}}{x - y}$ C、 $\frac{x - y}{x^{2} + y^{2}}$ D、 $\frac{5 x^{3}}{7 x^{5}}$

查看试题解析
9. 下列图形中有稳定性的是（）

A、等腰三角形 B、正方形 C、长方形 D、平行四边形

查看试题解析
10. 如图所示的正方形网格中，网格的交点称为格点，已知A ， B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形，则符合条件的点C的个数是（）

A、7 B、8 C、9 D、10

查看试题解析

二、填空题

11. 分解因式： $m^{3} - 4 m^{2} + 4 m$ ＝．

查看试题解析
12. 六边形的内角和是．

查看试题解析
13. 用科学记数法表示0.000000305＝．

查看试题解析
14. 若△ABC中，∠A＋∠B＝∠C ，则此三角形是三角形（填“锐角”“直角”或“钝角”）．

查看试题解析
15. 若分式 $\frac{x - 1}{x + 2}$ 的值为0，则x的值为．

查看试题解析
16. 如图，已知在Rt△ABC中，∠C＝90°．分别以A、B为圆心，大于 $\frac{1}{2}$ AB长为半径作弧，过弧的交点作直线，分别交AB于点D ，交AC于点E ．若∠A＝30°，CE＝1，BC＝ $\sqrt{3}$ ，则△ABE的面积为．

查看试题解析
17. 如图，已知在△ABC中，∠A=90°，AB=AC，CD平分∠ACB，DE⊥BC于E，若BC=15cm，则△DEB的周长为cm．

查看试题解析
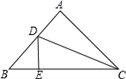18. 如图，AD是△ABC的角平分线，DE⊥AC ，垂足为E ， BF $//$ AC交ED的延长线于点F ，若BC恰好平分∠ABF ， AE＝2BF ，给出下列四个结论：①DE＝DF；②DB＝DC；③AD⊥BC；④AC＝3BF ， ⑤AC＝BC ．其中正确的结论有（填序号）．

查看试题解析

三、解答题

19. 计算：
$(3 x - 2) (2 x + 1) - 6 (x - 1) (x + 1)$

查看试题解析
20. 画图题（保留痕迹，不写画法，写出结论）
如图所示，边长为1的正方形网格中，△ABC的三个顶点A ， B ， C都在格点上．

作关于△ABC关于x轴的对称图形△DEF ，（其中A ， B ， C的对称点分别是D ， E ， F），并写出点D坐标．

查看试题解析
21. 先化简，再求值：
$(1 - \frac{1}{a + 2})$ ÷ $\frac{a^{2} - 1}{a + 2}$ ，其中 $a = {(\frac{1}{3})}^{- 1}$ ．

查看试题解析
22. 如图，点 $A$ 、 $C$ 、 $D$ 、 $B$ 在同一条直线上，且 $A C = B D$ ， $∠ A = ∠ B$ ， $∠ E = ∠ F$ .

(1)、求证： $△ A D E ≅ △ B C F$ .

(2)、若 $∠ B C F = 65 °$ ，求 $∠ C M D$ 的度数.

查看试题解析
23. 抗击新冠肺炎疫情期间，某口罩厂接到加大生产的紧急任务后积极扩大产能，现在每天生产的口罩比原来多4万个．已知现在生产100万个口罩所需的时间与原来生产60万个口罩所需的时间相同，求口罩厂原来每天生产多少万个口罩？

查看试题解析
24. 如图，点E在CD上，BC与AE交于点F，AB＝CB，BE＝BD，∠1＝∠2．

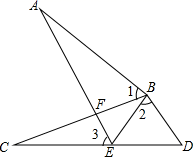(1)、求证：AE＝CD；

(2)、证明：∠1＝∠3．

查看试题解析
25. 如图，在等边三角形ABC中，点E是边AC上一定点，点D是直线BC上一动点，以DE为一边作等边三角形DEF ，连接CF ．

(1)、如图1，若点D在边BC上，直接写出CE ， CF与CD之间的数量关系；

(2)、如图2，若点D在边BC的延长线上，请探究线段CE ， CF与CD之间存在怎样的数量关系？并说明理由；

(3)、如图3，若点D在边CB的延长线上，请直接写出CE ， CF与CD之间的数量关系．

查看试题解析
26. 数学中，常对同一个量（图形的面积、点的个数等）用两种不同的方法计算，从而建立相等关系，我们把这种思想叫“算两次”．“算两次”也称作富比尼原理，是一种重要的数学思想，由它可以推导出很多重要的公式．

(1)、如图1，是一个长为 $2 a$ ，宽为 $2 b$ 的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图2的方式拼成一个正方形．
①用“算两次”的方法计算图2中阴影部分的面积：第一次列式为 ▲ ，第二次列式为 ▲ ，因为两次所列算式表示的是同一个图形的面积，所以可以得出等式 ▲ ；

②在①中，如果 $a + b = 7$ ， $a b = 10$ ，请直接用①题中的等式，求阴影部分的面积；

(2)、如图3，两个边长分别为a，b，c的直角三角形和一个两条直角边都是c的直角三角形拼成一个梯形，用“算两次”的方法，探究a，b，c之间的数量关系．

查看试题解析