辽宁省丹东市2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-05 类型:期末考试
一、单选题
-
1. 下列各数是无理数的是( )A、3.14 B、 C、-1.010010001 D、2. 将下列长度的三根木棒首尾顺次连接,能构成直角三角形的是( )A、1, ,2 B、5,12,15 C、4,5,6 D、 , ,53. 将三角形三个顶点的横坐标都减2,纵坐标不变,则所得三角形与原三角形的关系是( )A、将原图向左平移两个单位 B、关于原点对称 C、将原图向右平移两个单位 D、关于y轴对称4. 已知,直线a//b , 直角三角形如图放置,∠DCB=90°,若∠1+∠B=64°,则∠2的度数为( )
 A、20° B、26° C、30° D、35°5. 甲、乙、丙、丁四个小组的同学分别参加了班里组织的中华古诗词知识竞赛,在相同条件下各小组的成绩如下表所示,若要从中选择一个小组参加年级的比赛,那么应选( )
A、20° B、26° C、30° D、35°5. 甲、乙、丙、丁四个小组的同学分别参加了班里组织的中华古诗词知识竞赛,在相同条件下各小组的成绩如下表所示,若要从中选择一个小组参加年级的比赛,那么应选( )甲组
乙组
丙组
丁组
平均分
85
90
88
90
方差
3.5
3.5
4
4.2
A、甲组 B、乙组 C、丙组 D、丁组6. 下列命题是真命题的是( )A、在平面直角坐标系中,点P(﹣3,0)在y轴上 B、同位角相等 C、在一次函数y=3﹣2x中,y随着x的增大而增大 D、若 + =0,则x+y=﹣17. 已知正比例函数 的函数值随的增大而增大,则一次函数 的图象大致是( )A、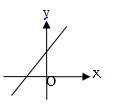 B、
B、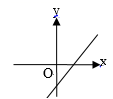 C、
C、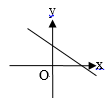 D、
D、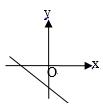 8. 如图,在Rt△ABC中,∠ACB=90°,AB=4.分别以AC,BC为直径作半圆,面积分别记为S1 , S2 , 则S1+S2的值等于( ).
8. 如图,在Rt△ABC中,∠ACB=90°,AB=4.分别以AC,BC为直径作半圆,面积分别记为S1 , S2 , 则S1+S2的值等于( ).
 A、2π B、3π C、4π D、8π9. 如图,小明和小丽练习跑步,两人分别从甲、乙两地同时出发,匀速相向而跑,小明的速度大于小丽的速度,小明到达乙地后,小丽继续跑至甲地.设出发x秒后,两人相距y米.图中折线表示从两人出发至小丽到达甲地的过程中,y与x的函数关系.下列说法中:
A、2π B、3π C、4π D、8π9. 如图,小明和小丽练习跑步,两人分别从甲、乙两地同时出发,匀速相向而跑,小明的速度大于小丽的速度,小明到达乙地后,小丽继续跑至甲地.设出发x秒后,两人相距y米.图中折线表示从两人出发至小丽到达甲地的过程中,y与x的函数关系.下列说法中:①甲乙两地相距900米;
②两人出发100秒后相遇;
③小丽的速度是4m/s;
④小明到达乙地,需要200秒.
其中正确的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
10. 7的平方根是 .11. 在平面直角坐标系中,点 (-3,4) 关于y轴对称的点的坐标是 .12. 8名初中毕业生的中考体育考试成绩(单位:分)如下:56,59,56,55,56,46,57,60,这些成绩的中位数是 .13. 在△ABC中,若∠A=66°,∠B=∠C , 则∠B= .14. 已知:若 的整数部分为a , 小数部分为b , 则3a﹣(b+3)2= .15. 如图,一次函数y=kx+b与y=x+2的图象相交于点P(m , 5),则方程组 的解是 .
 16. 如图所示,宽为50cm的矩形图案由10个全等的长方形拼成,其中一个小长方形的面积为.
16. 如图所示,宽为50cm的矩形图案由10个全等的长方形拼成,其中一个小长方形的面积为. 17. 如图,把 纸片沿 折叠,当点C落在四边形 的外部时,此时测得 ,则 .
17. 如图,把 纸片沿 折叠,当点C落在四边形 的外部时,此时测得 ,则 . 18. 在平面直角坐标系中,点A( ,0),点B(0,2 ),连接AB , 在第一象限内以AB为腰作等腰直角三角形ABC , 则线段OC的长为 .
18. 在平面直角坐标系中,点A( ,0),点B(0,2 ),连接AB , 在第一象限内以AB为腰作等腰直角三角形ABC , 则线段OC的长为 .三、解答题
-
19. 计算: .20. 解方程组: .21. 如图所示,在平面直角坐标系中,已知A(0,2),B(2,1),C(4,3),

⑴在平面直角坐标系中画出△ABC;
⑵在图中画出△ABC关于x轴对称的△A'B'C′,并写出C′的坐标( );
⑶已知P为y轴上一点,若△A′B′P的面积为3,请直接写出点P的坐标.
22. 如图,已知 , B. (1)、试判断DE与BC的位置关系,并说明理由(2)、若DE平分 , ,求 的度数.23. 丹东的草莓久负盛名,当下正是草莓的销售旺季,某日,我市一水果店以3650元购进两种不同品种的草莓,若按标价出售可获毛利润1600元(毛利润=售价﹣进价),这两种草莓的进价、标价如下表所示:
(1)、试判断DE与BC的位置关系,并说明理由(2)、若DE平分 , ,求 的度数.23. 丹东的草莓久负盛名,当下正是草莓的销售旺季,某日,我市一水果店以3650元购进两种不同品种的草莓,若按标价出售可获毛利润1600元(毛利润=售价﹣进价),这两种草莓的进价、标价如下表所示:价格/品种
A品种
B品种
进价(元/千克)
35
45
标价(元/千克)
50
65
求这两个品种的草莓各购进多少千克.
24. 习近平总书记指出“餐饮浪费现象,触目惊心,令人心痛”.为此我市某中学开展“厉行勤俭节约,反对铺张浪费”主题活动,为了解学生的参与情况,小明在全校范围内随机抽取了若干名学生就某日午饭浪费饭菜情况进行了调查.将调查内容分为四组:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据调查结果,绘制了如图所示两幅尚不完整的统计图,回答下列问题: (1)、这次被抽查的学生共有人,扇形统计图中,“B组”所对圆心角的度数为;(2)、补全条形统计图;(3)、已知该中学共有学生1500人,请估计这日午饭有剩饭的学生人数;若有剩饭的学生按平均每人剩20g米饭计算,这日午饭将浪费多少千克米饭.25. 甲、乙两组工人同时加工某种零件,甲组在工作中有一段时间停产更新设备,更新设备后,甲组的工作效率是原来的2倍.乙组工作2小时后,由于部分工人离开,工作效率有所降低.两组各自加工零件的数量y(件)与时间x(小时)之间的函数图象如图所示.
(1)、这次被抽查的学生共有人,扇形统计图中,“B组”所对圆心角的度数为;(2)、补全条形统计图;(3)、已知该中学共有学生1500人,请估计这日午饭有剩饭的学生人数;若有剩饭的学生按平均每人剩20g米饭计算,这日午饭将浪费多少千克米饭.25. 甲、乙两组工人同时加工某种零件,甲组在工作中有一段时间停产更新设备,更新设备后,甲组的工作效率是原来的2倍.乙组工作2小时后,由于部分工人离开,工作效率有所降低.两组各自加工零件的数量y(件)与时间x(小时)之间的函数图象如图所示.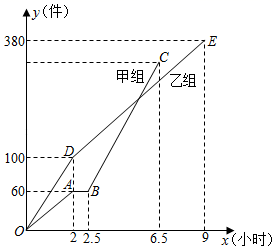 (1)、直接写出线段DE的函数关系式,并写出自变量的取值范围;(2)、求甲乙两组何时加工的零件数相同;(3)、若甲、乙两组加工的零件合在一起装箱,每320件装成一箱,零件装箱的时间忽略不计,直接写出经过多长时间恰好装满2箱.26. 如图所示,在平面直角坐标系中,点B的坐标为(4,8),过点B分别作BA⊥y轴,BC⊥x轴,得到一个长方形OABC , D为y轴上的一点,将长方形OABC沿着直线DM折叠,使得点A与点C重合,点B落在点F处,直线DM交BC于点E .
(1)、直接写出线段DE的函数关系式,并写出自变量的取值范围;(2)、求甲乙两组何时加工的零件数相同;(3)、若甲、乙两组加工的零件合在一起装箱,每320件装成一箱,零件装箱的时间忽略不计,直接写出经过多长时间恰好装满2箱.26. 如图所示,在平面直角坐标系中,点B的坐标为(4,8),过点B分别作BA⊥y轴,BC⊥x轴,得到一个长方形OABC , D为y轴上的一点,将长方形OABC沿着直线DM折叠,使得点A与点C重合,点B落在点F处,直线DM交BC于点E . (1)、直接写出点D的坐标;(2)、若点P为x轴上一点,是否存在点P使△PDE的周长最小?若存在,请求出△PDE的最小周长;若不存在,请说明理由.(3)、在(2)的条件下,若Q点是线段DE上一点(不含端点),连接PQ . 有一动点H从P点出发,沿线段PQ以每秒1个单位的速度运动到点Q , 再沿着线段QE以每秒 个单位长度的速度运动到点E后停止.请直接写出点H在整个运动过程中所用的最少时间t , 以及此时点Q的坐标.
(1)、直接写出点D的坐标;(2)、若点P为x轴上一点,是否存在点P使△PDE的周长最小?若存在,请求出△PDE的最小周长;若不存在,请说明理由.(3)、在(2)的条件下,若Q点是线段DE上一点(不含端点),连接PQ . 有一动点H从P点出发,沿线段PQ以每秒1个单位的速度运动到点Q , 再沿着线段QE以每秒 个单位长度的速度运动到点E后停止.请直接写出点H在整个运动过程中所用的最少时间t , 以及此时点Q的坐标.