辽宁省大连市西岗区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-05 类型:期末考试
一、单选题
-
1. 下列四个交通标志图中,是轴对称图形的是A、
 B、
B、 C、
C、 D、
D、 2. 若分式 有意义,则x的取值范围是( )A、x≠1 B、x>1 C、x=1 D、x<13. 下列运算正确的是( )A、 B、 C、 D、4. 一个多边形每一个外角都等于18°,则这个多边形的边数为( ).A、10 B、12 C、16 D、205. 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D.如果CE=12,则ED的长为( )
2. 若分式 有意义,则x的取值范围是( )A、x≠1 B、x>1 C、x=1 D、x<13. 下列运算正确的是( )A、 B、 C、 D、4. 一个多边形每一个外角都等于18°,则这个多边形的边数为( ).A、10 B、12 C、16 D、205. 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D.如果CE=12,则ED的长为( ) A、3 B、4 C、5 D、66. 如图,AC与BD交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC,还需( )
A、3 B、4 C、5 D、66. 如图,AC与BD交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC,还需( )
A、AB=DC B、OB=OC C、∠A=∠D D、∠AOB=∠DOC7. 下列各式由左边到右边的变形中,是分解因式的为( )A、 B、 C、 D、8. 若一个等腰三角形的两边长分别为 4,5,则这个等腰三角形的周长为( )A、13 B、14 C、13 或 14 D、8或 109. 计算 的结果是( )A、 B、 C、 D、10. A、B两港口相距n千米,一艘轮船往返于A、B两港口,如果轮船顺流航行的速度为a千米/小时,逆流航行的速度为b千米/小时,则轮船往返的平均速度是( )千米/小时.A、 B、 C、 D、二、填空题
-
11. 当 时,分式 的值为012. 分解因式: .13. 一粒米的质量是0.000026千克,0.000026用科学记数法表示为 .14. 如图,在 中, 是 的平分线, 交 于点E , 若 ,则 .
 15. 已知 , ,则 的值为 .16. 已知:如图, 中, ,D为 上一点, 于E , 若 ,则 .
15. 已知 , ,则 的值为 .16. 已知:如图, 中, ,D为 上一点, 于E , 若 ,则 .
三、解答题
-
17.(1)、计算:(2)、18.(1)、计算:(2)、解方程:19. 化简: ,并求出当 时的值.20. 如图:点 、 、 、 在一条直线上, 、 , ,

求证: .
21. 甲乙两人做某种机械零件,已知甲每小时比乙多做5个,甲做300个所用的时间与乙做200个所用的时间相等,求甲乙两人每小时各做几个零件?22. 如图, 三个顶点的坐标分别为 , , .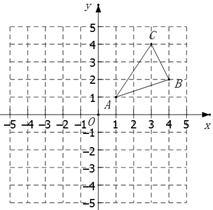
(1)请画出 关于x轴成轴对称的图形 ,并写出 、 、 的坐标;
(2)求 的面积;(3)在y轴上找一点P,使 的值最小,请画出点P的位置.
23. 一块原长分别为a、b( )的长方形,一边增加1,另一边减少1
 (1)、当 时,变化后的面积是增加还是减少?(2)、当 时,有两种方案,第一种方案如图1,第二种方案如图2,请你比较这两种方案,确定哪一种方案变化后的面积比较大.24. 如图:四边形 中, , , , .动点P从B向C以 的速度运动,动点Q由C向D运动.
(1)、当 时,变化后的面积是增加还是减少?(2)、当 时,有两种方案,第一种方案如图1,第二种方案如图2,请你比较这两种方案,确定哪一种方案变化后的面积比较大.24. 如图:四边形 中, , , , .动点P从B向C以 的速度运动,动点Q由C向D运动. (1)、若P、Q运动速度相等,运动1秒后,试判断 、 的数量关系,并说明理由;(2)、在P、Q运动过程中,若 与 全等,求Q点运动速度;(3)、若Q以 的速度运动,设运动时间为t, 的面积为S,请用含t的代数式表示S,并直接写出S最小值.25. 数学课上,刘老师出示了一道题,如图(一) 中, ,E为 上一点, 于D . 问:
(1)、若P、Q运动速度相等,运动1秒后,试判断 、 的数量关系,并说明理由;(2)、在P、Q运动过程中,若 与 全等,求Q点运动速度;(3)、若Q以 的速度运动,设运动时间为t, 的面积为S,请用含t的代数式表示S,并直接写出S最小值.25. 数学课上,刘老师出示了一道题,如图(一) 中, ,E为 上一点, 于D . 问:根据你所学的几何知识可以获取哪些结论?
小明抢着说:他知道哪个角等于 ;
阿强不甘落后说:若连结 ,他能求得 的度数.
思考了一会儿之后,小伟说:老师若添加 是 的平分线,我就能证得 .
老师非常的满意,同时提出:若 为 中线,大家试一试能否判断出 与 的数量关系呢?
同学们跃跃欲试,刘老师布置任务如下:
 (1)、直接写出与 相等的角;(2)、在图(一)中,求 的度数;(3)、在图(二)中若添加 为中线,判断 与 的数量关系.26. 如图1,在平面直角坐标系中,A、B坐标为(6,0)、(0,6),P为线段AB上的一点
(1)、直接写出与 相等的角;(2)、在图(一)中,求 的度数;(3)、在图(二)中若添加 为中线,判断 与 的数量关系.26. 如图1,在平面直角坐标系中,A、B坐标为(6,0)、(0,6),P为线段AB上的一点

 (1)、如图1,若S△AOP=12,求P的坐标(2)、如图2,若P为AB的中点,点M、N分别是OA、OB边上的动点,点M从顶点A、点N从顶点O同时出发,且它们的速度都为1 cm/s , 则在M、N运动的过程中,线段PM、PN之间有何关系?并证明(3)、如图3,若P为线段AB上异于A、B的任意一点,过B点作BD⊥OP , 交OP、OA分别与F、D两点,E为OA上一点,且∠PEA=∠BDO , 试判断线段OD与AE的数量关系,并说明理由
(1)、如图1,若S△AOP=12,求P的坐标(2)、如图2,若P为AB的中点,点M、N分别是OA、OB边上的动点,点M从顶点A、点N从顶点O同时出发,且它们的速度都为1 cm/s , 则在M、N运动的过程中,线段PM、PN之间有何关系?并证明(3)、如图3,若P为线段AB上异于A、B的任意一点,过B点作BD⊥OP , 交OP、OA分别与F、D两点,E为OA上一点,且∠PEA=∠BDO , 试判断线段OD与AE的数量关系,并说明理由