辽宁省朝阳市建平县2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-05 类型:期末考试
一、单选题
-
1. 下列实数中,是无理数的是( )A、3.14159265 B、 C、 D、2. 下列满足条件的三角形中,不是直角三角形的是( )A、三内角之比为1∶2∶3 B、三边长的平方之比为1∶2∶3 C、三边长之比为3∶4∶5 D、三内角之比为3∶4∶53. 若xy>0,则关于点P(x,y)的说法正确的是( )A、在一或二象限 B、在一或四象限 C、在二或四象限 D、在一或三象限4. 若方程组 的解是 ,则 的值分别是( )A、2,1 B、2,3 C、1,8 D、无法确定5. 下列图象中,可以表示一次函数 与正比例函数 (k,b为常数,且kb≠0)的图象的是( )A、
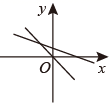 B、
B、 C、
C、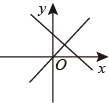 D、
D、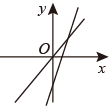 6. 如图,△ABC中,BO,CO分别是∠ABC,∠ACB的平分线,∠A=50°,则∠BOC等于( )
6. 如图,△ABC中,BO,CO分别是∠ABC,∠ACB的平分线,∠A=50°,则∠BOC等于( )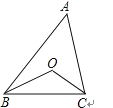 A、110° B、115° C、120° D、130°7. 小李家去年节余50000元,今年可节余95000元,并且今年收入比去年高15%,支出比去年低10%,今年的收入与支出各是多少?设去年的收入为x元,支出为y元,则可列方程组为( )A、 B、 C、 D、8. 如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )
A、110° B、115° C、120° D、130°7. 小李家去年节余50000元,今年可节余95000元,并且今年收入比去年高15%,支出比去年低10%,今年的收入与支出各是多少?设去年的收入为x元,支出为y元,则可列方程组为( )A、 B、 C、 D、8. 如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )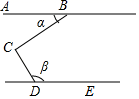 A、∠α+∠β=180° B、∠β﹣∠α=90° C、∠β=3∠α D、∠α+∠β=90°9. 下列命题中,是真命题的是( )A、算术平方根等于自身的数只有1 B、 ×|﹣1|×1是最简二次根式 C、只有一个角等于60°的三角形是等边三角形 D、三角形内角和等于180度10. 实数a,b在数轴上对应点的位置如图所示,且|a|>|b|,则化简 +|a+b|的结果为( )
A、∠α+∠β=180° B、∠β﹣∠α=90° C、∠β=3∠α D、∠α+∠β=90°9. 下列命题中,是真命题的是( )A、算术平方根等于自身的数只有1 B、 ×|﹣1|×1是最简二次根式 C、只有一个角等于60°的三角形是等边三角形 D、三角形内角和等于180度10. 实数a,b在数轴上对应点的位置如图所示,且|a|>|b|,则化简 +|a+b|的结果为( ) A、2a+b B、﹣2a﹣b C、b D、2a﹣b
A、2a+b B、﹣2a﹣b C、b D、2a﹣b二、填空题
-
11. 的立方根是 .12. 将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是.
 13. 已知点(﹣4,y1),(2,y2)都在直线y=﹣2x+2上,则y1、y2的大小关系是 .14. 甲、乙两名男同学练习投掷实心球,每人投了10次,平均成绩均为7.5米,方差分别为s甲2=0.2,S乙2=0.08,成绩比较稳定的是(填“甲”或“乙”).15. 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1<y2正确的是 .
13. 已知点(﹣4,y1),(2,y2)都在直线y=﹣2x+2上,则y1、y2的大小关系是 .14. 甲、乙两名男同学练习投掷实心球,每人投了10次,平均成绩均为7.5米,方差分别为s甲2=0.2,S乙2=0.08,成绩比较稳定的是(填“甲”或“乙”).15. 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1<y2正确的是 . 16. 已知10+ 的整数部分是x,小数部分是y,求x﹣y的相反数 .
16. 已知10+ 的整数部分是x,小数部分是y,求x﹣y的相反数 .三、解答题
-
17. 解方程组和计算(1)、计算:
①( ﹣2 ) × ﹣6 ;
②4( + )0+ × ﹣(1﹣ )2
(2)、解方程组:① ;
② .
18. 已知在平面直角坐标系中有 , , 三点,请回答下列问题:
(1)在坐标系内描出以 , , 三点为顶点的三角形.
(2)求 的面积.
(3)画出 关于x轴对称的图形19. 如图,已知CD∥BF,∠B+∠D=180°,求证:AB∥DE.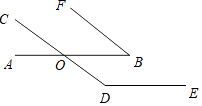 20. 列二元一次方程组解应用题:某大型超市投入15000元资金购进A、B两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:
20. 列二元一次方程组解应用题:某大型超市投入15000元资金购进A、B两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:类别/单价
成本价(元/箱
销售价(元/箱)
A品牌
20
32
B品牌
35
50
(1)、该大型超市购进A、B品牌矿泉水各多少箱?(2)、全部销售完600箱矿泉水,该超市共获得多少利润?21. 如图,在长方形ABCD中,DC=6cm,在DC上存在一点E,沿直线AE把△ADE折叠,使点D恰好落在BC边上的点F处,若△ABF的面积为24cm2 , 那么折叠的△ADE的面积为多少?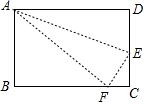 22. 如图,△ABC中,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,BD,CE交于点O,F,G分别是AC,BC延长线上一点,且∠EOD+∠OBF=180°,∠DBC=∠G,指出图中所有平行线,并说明理由.
22. 如图,△ABC中,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,BD,CE交于点O,F,G分别是AC,BC延长线上一点,且∠EOD+∠OBF=180°,∠DBC=∠G,指出图中所有平行线,并说明理由. 23. 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
23. 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
c
1.2
乙
7
b
8
d
(1)、写出表格中a,b,c,d的值;(2)、分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
