辽宁省本溪市2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，无理数是（）

A、 $\sqrt{4}$ B、 $- \frac{4}{3}$ C、0.333… D、 $- π$

查看试题解析
2. 在直角坐标系中，点A在y轴的右侧，在x轴的下方，距离每个坐标轴都是3个单位长度，则点A的坐标是（）

A、 $(3 ， 3)$ B、 $(3 ， - 3)$ C、 $(- 3 ， - 3)$ D、 $(- 3 ， 3)$

查看试题解析
3. 下列4组数中是勾股数的是（）

A、1.5，2.5，2 B、 $\sqrt{2}$ ， $\sqrt{2}$ ，2 C、12，16，20 D、0.5，1.2，1.3

查看试题解析
4. 下列命题：
①如果两个角相等，那么它们是对顶角；

②两直线平行，内错角相等；

③三角形的一个外角大于任何一个和它不相邻的内角；

④等腰三角形的底角必为锐角，其中假命题的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 下列函数的图象经过原点的是（）

A、 $y = - x + 1$ B、 $y = \frac{2}{x}$ C、 $y = 5 x$ D、 $y = - x^{2} + x + 1$

查看试题解析
6. 某中学八（1）班8个同学在课间进行一分钟跳绳比赛，成绩（单位：个）如下：115，138，126，143，134，126，157，118．这组数据的众数和中位数分别是（）

A、126，126 B、126，130 C、130，134 D、118，134

查看试题解析
7. 估计 $\sqrt{11.6}$ 的值在（）

A、3.2和3.3之间 B、3.3和3.4之间 C、3.4和3.5之间 D、3.5和3.6之间

查看试题解析
8. 一根旗杆在离地面3米处断裂，旗杆顶部落在离旗杆底部4米处，旗杆折断之前的高度是（）

A、5米 B、7米 C、8米 D、9米

查看试题解析
9. 小丽在本学期的数学成绩分别为：平时测验成绩为93分，期中考试成为90分，期末考试成绩为95分，按照平时、期中、期末所占比例为10%，30%，60%计算小丽本学期的总评成绩应该是（）

A、92.5分 B、92.8分 C、93.1分 D、93.3分

查看试题解析
10. 为了研究吸烟对肺癌是否有影响，某研究机构随机调查了8000人，结果显示：在吸烟者中患肺癌的比例是3%，在不吸烟者中患肺癌的比例是0.5%，吸烟者患肺癌的人数比不吸烟者患肺癌的人数多33人．在这8000人中，设吸烟者患肺癌的人数为x ，不吸烟者患肺癌的人数为y ．所列方程组正确的是（）

A、 ${\begin{array}{l} x - y = 33 \\ x \times 3 % + y \times 0.5 % = 8000 \end{array}$ B、 ${\begin{array}{l} x + y = 8000 \\ x \times 3 % - y \times 0.5 % = 22 \end{array}$ C、 ${\begin{array}{l} x - y = 33 \\ \frac{x}{3 %} + \frac{y}{0.5 %} = 8000 \end{array}$ D、 ${\begin{array}{l} x + y = 8000 \\ \frac{x}{3 %} - \frac{y}{0.5 %} = 33 \end{array}$

查看试题解析

二、填空题

11. $\sqrt{16}$ 的平方根是．

查看试题解析
12. 在 $R t Δ A B C$ 中，斜边AB=3．则 $A B^{2} + A C^{2} + B C^{2}$ =；

查看试题解析
13. 如图，直线a，b被直线c所截，a∥b，∠1=∠2，若∠3=40°，则∠4等于．

查看试题解析
14. ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ 是方程 $a x - y = 4$ 的解，则a的值是．

查看试题解析
15. 战士甲在射击比赛中，射击8次，命中的环数分别为：8，5，5，8，9，10，7，4，则这组数据的方差是．

查看试题解析
16. 已知 $a = \sqrt{5} + 2$ ， $b = \sqrt{5} - 2$ ，则 a²+b²+7 的算术平方根是．

查看试题解析
17. 在△ABC中，AB＝2 $\sqrt{2}$ ，BC＝1，∠ABC＝45°，以AB为一边作等腰直角三角形ABD，使∠ABD＝90°，连接CD，则线段CD的长为．

查看试题解析
18. 如图，在平面直角坐标系中，直线 $l$ ： $y = x + 2$ 交x轴于点A，交y轴于点 $A_{1}$ ，点 $A_{2}$ ， $A_{3}$ ，…在直线 $l$ 上，点 $B_{1}$ ， $B_{2}$ ， $B_{3}$ ，…在x轴的正半轴上，若 $Δ A_{1} O B_{1}$ ， $Δ A_{2} B_{1} B_{2}$ ， $Δ A_{3} B_{2} B_{3}$ ，…，依次均为等腰直角三角形，直角顶点都在x轴上，则第n个等腰直角三角形 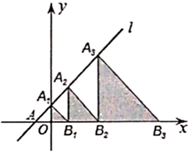$A_{n} B_{n - 1} B_{n}$ 顶点 $B_{n}$ 的横坐标为．

查看试题解析

三、解答题

19.

(1)、计算： $\sqrt[3]{8} + \sqrt{32} - 6 \sqrt{\frac{1}{2}} - {(π - 3)}^{0}$

(2)、解方程组： ${\begin{array}{l} 3 x - 4 y = 2 \\ \frac{x}{3} - \frac{y}{4} = 1 \end{array}$

(3)、如下图，在平面直角坐标系中， $△ A B C$ 的三个顶点分别为 $A (2 ， 3)$ ， $B (3 ， 1)$ ， $C (- 2 - 1)$ ．

①请在图中作出 $△ A B C$ 关于y轴对称的 $△ A^{'} B^{'} C^{'}$ 并直接写出 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 的坐标；

②作点A关于x轴的对称点D ，直接写出四边形ABDC的面积．

查看试题解析
20. 如图，已知在 $△ A B C$ 中， $A B = 25$ ， $B C = 14$ ，BC边上的中线 $A D = 24$ ．求证： $A B = A C$ ．

查看试题解析
21. 随着经济的快速发展，环境问题越来越受到人们的关注，某校学生会为了解节能减排、垃圾分类知识的普及情况，随机调查了部分学生，调查结果分为“A．非常了解”“B．了解”“C了解较少”“D．不了解”四类，每名学生从中选择并且只能选择一类，并将调查结果绘制成如下两个统计图．

(1)、本次接受随机调查的学生人数为，扇形图中m的值为；

(2)、本次调查获取的A，B，C，D四类对应的人数的平均数为，中位数为；

(3)、根据样本数据，估计该校1200名学生中，D类学生有多少人？

查看试题解析
22. 某公司在手机网络平台推出的一种新型打车方式受到大众的欢迎，该打车方式的总费用由里程费和耗时费组成，其中里程费按x元/千米计算，耗时费按y元/分钟计算．小聪、小明两人用该打车方式出行，按上述计价规则，他们打车行驶里程数、所用时间及支付车费如下表：

里程数（千米）

时间（分钟）

车费（元）

小聪

3

10

9

小明

6

18

17.4

(1)、求x ， y的值；

(2)、该公司现推出新政策，在原有付费基础上，当里程数超过8千米后，超出的部分要加收0.6元/千米的里程费，小强使用该方式从家打车到郊区，总里程为23千米，耗时30分钟，求小强需支付多少车费．

查看试题解析
23. 甲、乙两人同时从相距90千米的A地前往B地，甲乘汽车，乙骑电动车，甲到达B地停留半个小时后返回A地，如图是他们离A地的距离y（千米）与经过时间x（小时）之间的函数关系图象．

(1)、甲从B地返回A地的过程中，直接写出y与x之间的函数关系式及自变量x的取值范围；

(2)、若乙出发后108分钟和甲相遇，求乙从A地到B地用了多少分钟？

(3)、甲与乙同时出发后，直接写出经过多长时间他们相距20千米？

查看试题解析
24. 已知点A在射线CE上， $∠ B D A = ∠ C$ ．

(1)、如图1，若 $A C$ // $B D$ ，求证： $A D$ // $B C$ ；

(2)、如图2，若 $∠ B A C = ∠ B A D$ ， $B D ⊥ B C$ ，请证明 $∠ D A E + 2 ∠ C = 90 °$ ；

(3)、如图3，在（2）的条件下，过点D作 $D F$ // $B C$ 交射线CE于点F ，当 $∠ D F E = 8 ∠ D A E$ 时，求 $∠ B A D$ 的度数．（直接写出结果）

查看试题解析
25. 如图所示，在平面直角坐标系中，直线 $y = - \frac{1}{2} x + 3$ 分别与x轴、y轴交于点B ， C ，且与直线 $y = \frac{1}{2} x - 2$ 交于点A ，直线 $y = \frac{1}{2} x - 2$ 与y轴交于点D．

(1)、直接写出点A ， B ， C ， D的坐标；

(2)、若点E是直线AD上的点，且 $△ C O E$ 的面积为12，求直线CE的函数表达式；

(3)、设点P是x轴上的点，使得点P到点A ， C的距离和最小，直接写出点P的坐标．

查看试题解析

	里程数（千米）	时间（分钟）	车费（元）
小聪	3	10	9
小明	6	18	17.4