江西省南昌市2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-05 类型:期末考试
一、单选题
-
1. 若分式 有意义,则x的取值范围是( )A、 B、 C、 D、2. 下列等式中,运算正确的是( ).A、 B、 C、 D、3. 如图, 中, , ,垂足为D , ,交 于点E , 若 ,则 的长为( ).
 A、4 B、5 C、6 D、74. 将一个四边形 的纸片剪去一个三角形,则剩下图形的内角和为( ).A、180° B、180°或360° C、360°或540° D、180°或360°或540°5. 若分式 运算结果为x,则在“□”中添加的运算符号为( )A、+ B、- C、-或÷ D、+或×6. 4张长为a、宽为 的长方形纸片,按如图的方式拼成一个边长为 的正方形,图中空白部分的面积为 ,阴影部分的面积为 .若 ,则a、b满足( )
A、4 B、5 C、6 D、74. 将一个四边形 的纸片剪去一个三角形,则剩下图形的内角和为( ).A、180° B、180°或360° C、360°或540° D、180°或360°或540°5. 若分式 运算结果为x,则在“□”中添加的运算符号为( )A、+ B、- C、-或÷ D、+或×6. 4张长为a、宽为 的长方形纸片,按如图的方式拼成一个边长为 的正方形,图中空白部分的面积为 ,阴影部分的面积为 .若 ,则a、b满足( )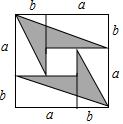 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 计算: .8. 等腰三角形的一个外角是80°,则这个等腰三角形的底角度数是.9. 如图,点F是△ABC的边BC延长线上一点,DF⊥AB于点D , ∠A=30°,∠F=40°,∠ACF的度数是 .
 10. 化简: .11. 如图,在平面直角坐标系中,四边形 为正方形,点A的坐标 , ,则点C的坐标为 .
10. 化简: .11. 如图,在平面直角坐标系中,四边形 为正方形,点A的坐标 , ,则点C的坐标为 . 12. 若分式 的值为正整数,则整数x的值为 .
12. 若分式 的值为正整数,则整数x的值为 .三、解答题
-
13. 计算:(1)、 ;(2)、 .14. 解分式方程: .15. 先化简, ,再从 ,2中选择一个合适的数代入求值.16. 已知 , ,求下列各代数式的值:(1)、 ;(2)、 .17. 从三个整式;① ,② ,③ 中,任意选择两个分别作为一个分式的分子和分母.(1)、一共能得到个不同的分式;(2)、这些分式化简后结果为整式的分式有哪些?并写出化简结果.18. “垃圾分一分,环境美十分”,分类垃圾桶成为我们生活中的必备工具.某学校开学初购进A型和B型两种分类垃圾桶,购买A型垃圾桶花费了2500元,购买B型垃圾桶花费了2000元,且购买A型垃圾桶数量是购买B型垃圾桶数量的2倍,已知购买一个B型垃圾桶比购买一个A型垃圾桶多花30元.(1)、求购买一个A型垃圾桶,B型垃圾桶各需多少元?(2)、由于实际需要,学校决定再次购买与第一次同样数量的A型和B型两种分类垃圾桶,恰逢市场对这两种垃圾桶的售价进行调整,A型垃圾桶售价比第一次购买时提高了10%,B型垃圾桶按第一次购买时售价的9折出售,第二次购买A型和B型两种分类垃圾桶一共花了多少钱?19. 观察下列关于自然数的等式:
第1个等式: ;
第2个等式: ;
第3个等式: ;
第4个等式: ;
……
根据上述规律解决下列问题:
(1)、写出第5个等式;(2)、写出你猜想的第n个等式(用含n的式子表示),并验证你写的等式;(3)、在这n个等式中,等式右边结果能否是2021?请说明理由.20. 定义:若两个分式的和为n(n为正整数),则称这两个分式互为“n和分式”.例如: ,我们称两个分式 与 互为“5和分式”.解答下列问题:(1)、分式 与分式互为“4和分式”;(2)、分式 与分式 互为“和分式”;(3)、已知 ,两个分式 与 是否是“n和分式”?如果是,请求出n的值;如果不是,请说明理由;(4)、若分式 与 互为“3和分式”(其中x , y为正数),求 的值.21. 有三个面积都等于1的三角形,它们的底及对应的高分别记为: , , 及 , , .(1)、 , , .如果 ,则用 , , 填空:<<;
(2)、如果 , , ( ),试比较 , 的大小;(3)、如果 , , ( ).求 的值(用含n的代数式表示).