江西省赣州市章贡区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-05 类型:期末考试
一、单选题
-
1. 垃圾分类功在当代利在千秋,如图垃圾分类指引标志图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 现有两根木棒,它们的长分别是 和 ,若要钉成一个三角形木架,则应选取的第三根木棒长可以为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、(a+b)2=a2+b24. 如图是“一带一路”示意图,若记北京为 地,莫斯科为 地,雅典为 地,分别连接 , , ,形成一个三角形,若想建立一个货物中转仓,使其到 三地的距离相等,则中转仓的位置应选在( )
2. 现有两根木棒,它们的长分别是 和 ,若要钉成一个三角形木架,则应选取的第三根木棒长可以为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、(a+b)2=a2+b24. 如图是“一带一路”示意图,若记北京为 地,莫斯科为 地,雅典为 地,分别连接 , , ,形成一个三角形,若想建立一个货物中转仓,使其到 三地的距离相等,则中转仓的位置应选在( )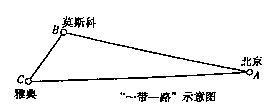 A、 三条中线的交点处 B、 三边的垂直平分线的交点处 C、 三条角平分线的交点处 D、 三条高所在直线的交点处5. 将分式 中 的值都扩大到原来的3倍,则扩大后分式的值( )A、扩大到原来的3倍 B、扩大到原来的9倍 C、不变 D、缩小到原来的6. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
A、 三条中线的交点处 B、 三边的垂直平分线的交点处 C、 三条角平分线的交点处 D、 三条高所在直线的交点处5. 将分式 中 的值都扩大到原来的3倍,则扩大后分式的值( )A、扩大到原来的3倍 B、扩大到原来的9倍 C、不变 D、缩小到原来的6. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )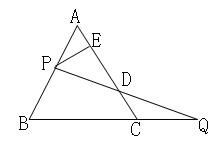 A、 B、 C、 D、不能确定
A、 B、 C、 D、不能确定二、填空题
-
7. 因式分解:2a2﹣8= .8. 当x=时,分式 值为0.9. 已知10a=2,10b=3,则102a+3b= .10. 如图,AE=DF , ∠A=∠D , 欲证ΔACE≌ΔDBF , 需要添加条件 , 证明全等的理由是 .
 11. 如图,在Rt△ABC中,∠A=90°,∠C=30°,AB=1,AC= ,E、F分别是AC、BC上的动点,则BE+EF的最小值是 .
11. 如图,在Rt△ABC中,∠A=90°,∠C=30°,AB=1,AC= ,E、F分别是AC、BC上的动点,则BE+EF的最小值是 . 12. 如图,在△ABC中,∠ACB=90°,AC=5cm , BC=12cm . 动点P从A点出发沿A→C的路径向终点C运动;动点Q从B点出发沿B→C→A路径向终点A运动.点P和点Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过点P和Q作PE⊥MN于E , QF⊥MN于F . 则点P运动时间为秒时,△PEC与△QFC全等.
12. 如图,在△ABC中,∠ACB=90°,AC=5cm , BC=12cm . 动点P从A点出发沿A→C的路径向终点C运动;动点Q从B点出发沿B→C→A路径向终点A运动.点P和点Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过点P和Q作PE⊥MN于E , QF⊥MN于F . 则点P运动时间为秒时,△PEC与△QFC全等.
三、解答题
-
13.(1)、计算:(2 ﹣1)0﹣|﹣6|+( )﹣2(2)、计算:(a+1)(a﹣1)﹣(a﹣2)214. 解分式方程:15. 先化简,再求值: ,其中a满足 .16. 如图,点E在AB上,△ABC≌△DEC,求证:CE平分∠BED.
 17. 如图,在△ABC中,已知AB=AC , AD⊥BC于点D , 请仅用无刻度的直尺按要求画图.
17. 如图,在△ABC中,已知AB=AC , AD⊥BC于点D , 请仅用无刻度的直尺按要求画图.
(1)如图①,点P为AB上任意一点,在AC上找出一点P',使AP=AP';
(2)如图②,点P为BD上任意一点,在CD上找出一点P',使BP=CP'.18. △ABC在平面直角坐标系中的位置如图所示,先将△ABC向右平移3个单位,再向下平移1个单位到△A1B1C1 , △A1B1C1和△A2B2C2关于x轴对称. (1)、画出△A1B1C1和△A2B2C2;(2)、在x轴上确定一点P , 使BP+A1P的值最小,直接写出P的坐标为;(3)、点Q在y轴上且满足△ACQ为等腰三角形,则这样的Q点有个.19. 已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)、画出△A1B1C1和△A2B2C2;(2)、在x轴上确定一点P , 使BP+A1P的值最小,直接写出P的坐标为;(3)、点Q在y轴上且满足△ACQ为等腰三角形,则这样的Q点有个.19. 已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点. (1)、求∠EDA的度数;(2)、AB=10,AC=8,DE=3,求S△ABC .20. 某中学教学楼需要在规定时间内改造完以迎接新学期的开学,在工程招标时,接到甲、乙两个工程队的投标书如表(部分信息):
(1)、求∠EDA的度数;(2)、AB=10,AC=8,DE=3,求S△ABC .20. 某中学教学楼需要在规定时间内改造完以迎接新学期的开学,在工程招标时,接到甲、乙两个工程队的投标书如表(部分信息):甲:(1)施工一天,需付甲工程队2.1万元;
(1)、学校规定的期限是多少天?(2)、在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.21. 阅读下列材料利用完全平方公式,将多项式x2+bx+c变形为(x+m)2+n的形式.
例如:x2﹣8x+17=x2﹣2•x•4+42﹣42+17=(x﹣4)2+1
(1)、填空:将多项式x2﹣2x+3变形为(x+m)2+n的形式,并判断x2﹣2x+3与0的大小关系.∵x2﹣2x+3=(x﹣)2+ .
∴x2﹣2x+30(填“>”、“<”、“=”)
(2)、如图①所示的长方形边长分别是2a+5、3a+2,求长方形的面积S1(用含a的式子表示);如图②所示的长方形边长分别是5a、a+5,求长方形的面积S2(用含a的式子表示) (3)、比较(2)中S1与S2的大小,并说明理由.22. 已知,如图AD为△ABC的中线,分别以AB和AC为一边在△ABC的外部作等腰三角形ABE和等腰三角形ACF , 且AE=AB , AF=AC , 连接EF , ∠EAF+∠BAC=180°
(3)、比较(2)中S1与S2的大小,并说明理由.22. 已知,如图AD为△ABC的中线,分别以AB和AC为一边在△ABC的外部作等腰三角形ABE和等腰三角形ACF , 且AE=AB , AF=AC , 连接EF , ∠EAF+∠BAC=180° (1)、如图1,若∠ABE=63°,∠BAC=45°,求∠FAC的度数;(2)、如图1请探究线段EF和线段AD有何数量关系?并证明你的结论;(3)、如图2,设EF交AB于点G , 交AC于点R , 延长FC , EB交于点M , 若点G为线段EF的中点,且∠BAE=70°,请探究∠ACB和∠CAF的数量关系,并证明你的结论.23. 如图1,点A和点B分别在y轴正半轴和x轴负半轴上,且OA=OB,点C和点D分别在第四象限和第一象限,且OC⊥OD,OC=OD,点D的坐标为(m,n),且满足 +|n﹣2|=0.
(1)、如图1,若∠ABE=63°,∠BAC=45°,求∠FAC的度数;(2)、如图1请探究线段EF和线段AD有何数量关系?并证明你的结论;(3)、如图2,设EF交AB于点G , 交AC于点R , 延长FC , EB交于点M , 若点G为线段EF的中点,且∠BAE=70°,请探究∠ACB和∠CAF的数量关系,并证明你的结论.23. 如图1,点A和点B分别在y轴正半轴和x轴负半轴上,且OA=OB,点C和点D分别在第四象限和第一象限,且OC⊥OD,OC=OD,点D的坐标为(m,n),且满足 +|n﹣2|=0. (1)、求点D的坐标;(2)、求∠AKO的度数;(3)、如图2,点P,Q分别在y轴正半轴和x轴负半轴上,且OP=OQ,直线ON⊥BP交AB于点N,MN⊥AQ交BP的延长线于点M,判断ON,MN,BM的数量关系并证明.
(1)、求点D的坐标;(2)、求∠AKO的度数;(3)、如图2,点P,Q分别在y轴正半轴和x轴负半轴上,且OP=OQ,直线ON⊥BP交AB于点N,MN⊥AQ交BP的延长线于点M,判断ON,MN,BM的数量关系并证明.