山东省淄博市沂源县2020-2021学年六年级下学期数学期末试卷(五四学制)
试卷更新日期:2021-11-05 类型:期末考试
一、选择题:本大题共12个小题,每小题5分,共60分.
-
1. 下列计算正确的是( )A、a4+a5=a9 B、a3•a3•a3=3a3 C、(﹣a3)4=a7 D、2a4•3a5=6a92. (a﹣b+c)(﹣a+b﹣c)等于( )A、﹣(a﹣b+c)2 B、c2﹣(a﹣b)2 C、(a﹣b)2﹣c2 D、c2﹣a+b23. 下列调查方式,你认为最合适的是( )A、日光灯管厂要检测一批灯管的使用寿命,采用普查方式 B、了解我市每天的流动人口数,采用抽样调查方式 C、疫情期间了解入校的同学的体温,采用抽样调查方式 D、旅客上飞机前的安检,采用抽样调查方式4. 已知两个变量x和y,它们之间的3组对应值如表所示,
x
﹣1
0
1
y
3
2
1
则y与x之间的关系式可能是( )
A、y=x B、y=x2+x+1 C、y=﹣x+2 D、y=5. 如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,则图中与∠AGE相等的角( ) A、2个 B、3个 C、4个 D、5个6. 已知a=255 , b=344 , c=433 , 则a、b、c的大小关系是( )A、b>c>a B、a>b>c C、c>a>b D、a<b<c7. 若代数式M•(3x﹣y2)=y4﹣9x2 , 那么代数式M为( )A、﹣3x﹣y2 B、﹣3x+y2 C、3x+y2 D、3x﹣y28. 如图,现将一块三角板的含有60°的角的顶点放在直尺的一边上,若∠1=80°,那么∠2的度数为( )
A、2个 B、3个 C、4个 D、5个6. 已知a=255 , b=344 , c=433 , 则a、b、c的大小关系是( )A、b>c>a B、a>b>c C、c>a>b D、a<b<c7. 若代数式M•(3x﹣y2)=y4﹣9x2 , 那么代数式M为( )A、﹣3x﹣y2 B、﹣3x+y2 C、3x+y2 D、3x﹣y28. 如图,现将一块三角板的含有60°的角的顶点放在直尺的一边上,若∠1=80°,那么∠2的度数为( )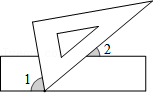 A、30° B、40° C、50° D、60°9. 为了了解乐山市2018年中考数学学科各分数段成绩分布情况,从中抽取300名考生的中考数学成绩进行统计分析,在这个问题中,样本是指( )A、300 B、抽取的300名考生 C、抽取的300名考生的中考数学成绩 D、乐山市2018年中考数学成绩10. 在如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A、30° B、40° C、50° D、60°9. 为了了解乐山市2018年中考数学学科各分数段成绩分布情况,从中抽取300名考生的中考数学成绩进行统计分析,在这个问题中,样本是指( )A、300 B、抽取的300名考生 C、抽取的300名考生的中考数学成绩 D、乐山市2018年中考数学成绩10. 在如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )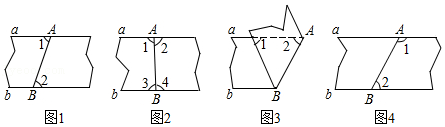 A、如图1,展开后测得∠1=∠2 B、如图3,测得∠1=∠2 C、如图2,展开后测得∠1=∠2且∠3=∠4 D、在图4,展开后测得∠1+∠2=180°11. 早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途中的时间为x,两人之间的距离为y,则下列选项中的图象能大致反映y与x之间关系的是( )A、
A、如图1,展开后测得∠1=∠2 B、如图3,测得∠1=∠2 C、如图2,展开后测得∠1=∠2且∠3=∠4 D、在图4,展开后测得∠1+∠2=180°11. 早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途中的时间为x,两人之间的距离为y,则下列选项中的图象能大致反映y与x之间关系的是( )A、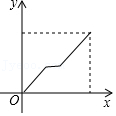 B、
B、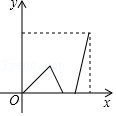 C、
C、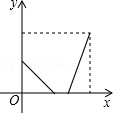 D、
D、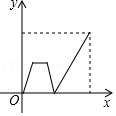 12. 仔细观察,探索规律:
12. 仔细观察,探索规律:(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(x﹣1)(x4+x3+x2+x+1)=x5﹣1
…
则22020+22019+22018+22017+…+2+1的个位数字是( )
A、1 B、3 C、5 D、7二、填空题:本题共5小题,每小题4分,共20分,
-
13. 计算:(a﹣b)•(b﹣a)2=(结果用幂的形式表示).14. 如图,要把池中的水引到D处,可过D点引DC⊥AB于C,然后沿DC开渠,可使所开渠道最短,试说明设计的依据: .
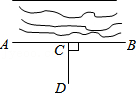 15. 某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间修建一座边长是(a+b)米的正方形雕像.请用含a,b的代数式表示绿化面积 .
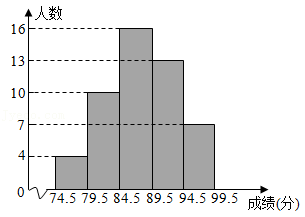
15. 某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间修建一座边长是(a+b)米的正方形雕像.请用含a,b的代数式表示绿化面积 .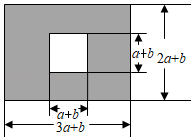 16. 为了了解某地九年级学生参加消防知识竞赛成绩(均为整数),从中抽取了1%的同学的竞赛成绩,整理后绘制了如下的频数分布直方图,请结合图形解答下列问题:
16. 为了了解某地九年级学生参加消防知识竞赛成绩(均为整数),从中抽取了1%的同学的竞赛成绩,整理后绘制了如下的频数分布直方图,请结合图形解答下列问题:若竞赛成绩在90分以上的同学可以获得奖励,则估计该地获得奖励的九年级学生约有人.
 17. 一种豆子在市场上出售,豆子的总销售额(单位:元)与所售豆子的质量(单位:千克)之间的数量关系如下表所示:
17. 一种豆子在市场上出售,豆子的总销售额(单位:元)与所售豆子的质量(单位:千克)之间的数量关系如下表所示:所售豆子质量(千克)
0
0.5
1
1.5
2
2.5
3
3.5
4
销售额(元)
0
1
2
3
4
5
6
7
8
根据你的预测,出售千克豆子,可得销售额21元.
三、解答题:本大题共7小题,共70分.
-
18. 计算:(1)、(x﹣y)2(y﹣x)5+(x﹣y)3(y﹣x)4;(2)、﹣12x3y4÷(﹣3x2y3)•(xy);(3)、(54x2y﹣108xy2﹣36xy)÷(18xy);(4)、972+20162﹣2015×2017(用乘法公式简算).19. 如图,在8×8的正方形网格中,每个小正方形的顶点称为格点,小正方形的边长为1,点P是∠AOB的边OB上的一点,点M是∠AOB内部的一点,点A、B、M、O、P均在格点上,只用无刻度的直尺,在给定的网格中按要求画图,并填空.
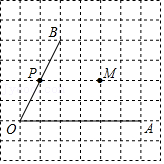
⑴过点M画OA的平行线MN.
⑵过点P画OB的垂线PC,交OA于点C.
⑶点C到直线MN的距离为 .
20. 已知:如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.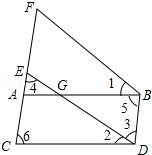 21. 如图,直线AB上有一点P,点M,N分别为线段PA,PB的中点,AB=14.
21. 如图,直线AB上有一点P,点M,N分别为线段PA,PB的中点,AB=14.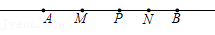 (1)、若点P在线段AB上,且AP=8,求线段MN的长度;(2)、若点P在直线AB上运动,设AP=x,BP=y,请分别计算下面情况时MN的长度:
(1)、若点P在线段AB上,且AP=8,求线段MN的长度;(2)、若点P在直线AB上运动,设AP=x,BP=y,请分别计算下面情况时MN的长度:①当P在AB之间;
②当P在A左边;
⑧当P在B右边;
你发现了什么规律?
22. 某商场对一种新售的手机进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(不比较喜欢)、D(非常喜欢)四个等级对该手机进行评价,图①和图②是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题: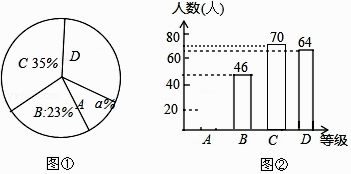 (1)、本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.(2)、图①中,a等于多少?D等级所占的圆心角为多少度?23. 小凡与小光从学校出发到距学校5千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图反映了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题:
(1)、本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.(2)、图①中,a等于多少?D等级所占的圆心角为多少度?23. 小凡与小光从学校出发到距学校5千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图反映了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题: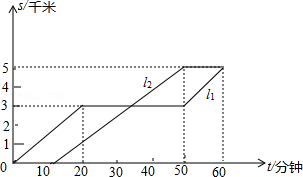 (1)、l1和l2哪一条是描述小凡的运动过程,说说你的理由;(2)、小凡和小光谁先出发,先出发了多少分钟?(3)、小凡与小光谁先到达图书馆,先到了多少分钟?(4)、小凡与小光从学校到图书馆的平均速度各是多少千米/小时?(不包括中间停留的时间)24. 已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD.
(1)、l1和l2哪一条是描述小凡的运动过程,说说你的理由;(2)、小凡和小光谁先出发,先出发了多少分钟?(3)、小凡与小光谁先到达图书馆,先到了多少分钟?(4)、小凡与小光从学校到图书馆的平均速度各是多少千米/小时?(不包括中间停留的时间)24. 已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD.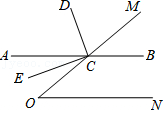 (1)、若∠O=50°,求∠BCD的度数;(2)、求证:CE平分∠OCA;(3)、当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.
(1)、若∠O=50°,求∠BCD的度数;(2)、求证:CE平分∠OCA;(3)、当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.