山东省烟台市福山区2020-2021学年六年级下学期数学期末试卷(五四学制)
试卷更新日期:2021-11-05 类型:期末考试
一、选择题(共12小题,每小题3分,共36分)
-
1. 下列运算正确的是( )A、m+2m=3m2 B、2m3•3m2=6m6 C、(2m)3=8m3 D、m6÷m2=m32. 如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是( )
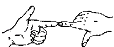 A、同位角 B、内错角 C、对顶角 D、同旁内角3. 2020年6月3日9时43分,“北斗三号”最后一颗全球组网卫星发射成功,它的授时精度小于0.00000002s,则0.00000002用科学记数法表示为( )A、0.2×10﹣6 B、0.2×10﹣7 C、2×10﹣7 D、2×10﹣84. 小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )A、
A、同位角 B、内错角 C、对顶角 D、同旁内角3. 2020年6月3日9时43分,“北斗三号”最后一颗全球组网卫星发射成功,它的授时精度小于0.00000002s,则0.00000002用科学记数法表示为( )A、0.2×10﹣6 B、0.2×10﹣7 C、2×10﹣7 D、2×10﹣84. 小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )A、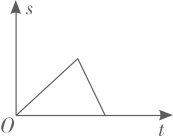 B、
B、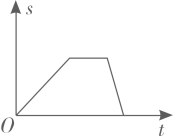 C、
C、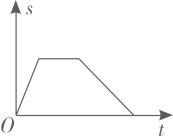 D、
D、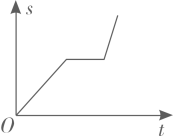 5. 下列问题中,采用的调查方式合适的是( )A、调查全国初中学生视力情况,采用普查方式 B、了解某班同学“仰卧起坐”的成绩情况,采用抽样调查方式 C、调查一批西瓜甜度情况,采用普查方式 D、调查2021年央视“党史大赛”节目的收视率,采用抽样调查方式6. 如图,已知BE平分∠ABC , 且BE∥DC , 若∠ABC=50°,则∠C的度数是( )
5. 下列问题中,采用的调查方式合适的是( )A、调查全国初中学生视力情况,采用普查方式 B、了解某班同学“仰卧起坐”的成绩情况,采用抽样调查方式 C、调查一批西瓜甜度情况,采用普查方式 D、调查2021年央视“党史大赛”节目的收视率,采用抽样调查方式6. 如图,已知BE平分∠ABC , 且BE∥DC , 若∠ABC=50°,则∠C的度数是( )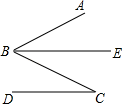 A、20° B、25° C、30° D、50°7. 根据如图所示的程序计算函数y的值,若输入x的值是7,则输出y的值是﹣2,若输入x的值是﹣8,则输出y的值是( )
A、20° B、25° C、30° D、50°7. 根据如图所示的程序计算函数y的值,若输入x的值是7,则输出y的值是﹣2,若输入x的值是﹣8,则输出y的值是( ) A、5 B、10 C、19 D、218. 数轴上点A,B,M表示的数分别是a,2a,9,点M为线段AB的中点,则a的值是( )A、3 B、4.5 C、6 D、189. 如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是( )
A、5 B、10 C、19 D、218. 数轴上点A,B,M表示的数分别是a,2a,9,点M为线段AB的中点,则a的值是( )A、3 B、4.5 C、6 D、189. 如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是( ) A、∠BAO与∠CAO相等 B、∠BAC与∠ABD互补 C、∠BAO与∠ABO互余 D、∠ABO与∠DBO不等10. 如图,已知∠AOB与∠EO′F,分别以O,O′为圆心,以同样长为半径画弧,分别交OA,OB于点A′,B′,交O′E,O′F于点E′,F′,以B′为圆心,以E′F′长为半径画弧,交弧A′B′于点A″.下列结论错误的是( )
A、∠BAO与∠CAO相等 B、∠BAC与∠ABD互补 C、∠BAO与∠ABO互余 D、∠ABO与∠DBO不等10. 如图,已知∠AOB与∠EO′F,分别以O,O′为圆心,以同样长为半径画弧,分别交OA,OB于点A′,B′,交O′E,O′F于点E′,F′,以B′为圆心,以E′F′长为半径画弧,交弧A′B′于点A″.下列结论错误的是( ) A、∠AOB=2∠EO′F B、∠AOB>∠EO′F C、∠A″OB=∠EO′F D、∠AOA″=∠AOB﹣∠EO′F11. 为了调查疫情对青少年人生观、价值观产生的影响,某学校团委对初一级部学生进行了问卷调查,其中一项是:疫情期间出现的哪一个高频词汇最触动你的内心?针对该项调查结果制作的两个统计图(不完整)如图.由图中信息可知,下列结论错误的是( )
A、∠AOB=2∠EO′F B、∠AOB>∠EO′F C、∠A″OB=∠EO′F D、∠AOA″=∠AOB﹣∠EO′F11. 为了调查疫情对青少年人生观、价值观产生的影响,某学校团委对初一级部学生进行了问卷调查,其中一项是:疫情期间出现的哪一个高频词汇最触动你的内心?针对该项调查结果制作的两个统计图(不完整)如图.由图中信息可知,下列结论错误的是( ) A、选“责任”的有120人 B、本次调查的样本容量是600 C、选“感恩”的人数最多 D、扇形统计图中“生命”所对应的扇形圆心角度数为64.8°12. 将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )
A、选“责任”的有120人 B、本次调查的样本容量是600 C、选“感恩”的人数最多 D、扇形统计图中“生命”所对应的扇形圆心角度数为64.8°12. 将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )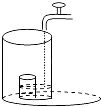 A、
A、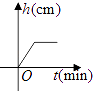 B、
B、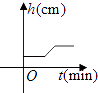 C、
C、 D、
D、
二、填空题(共6个小题,每小题3分,满分18分)
-
13. 若xm=15,xn=5,则xm﹣n等于 .14. 若a+b=1,则a2﹣b2+2b﹣2= .15. 如图,一块长为m,宽为n的长方形草坪,上下开辟的花园,都是由等半径的两个四分之一圆和一个半圆组成,那么中间草坪的面积是 .
 16. 如图,点B,C在直线l上,且BC=6cm,△ABC的面积为18cm2 . 若P是直线l上任意一点,连接AP,则线段AP的最小长度为cm.
16. 如图,点B,C在直线l上,且BC=6cm,△ABC的面积为18cm2 . 若P是直线l上任意一点,连接AP,则线段AP的最小长度为cm.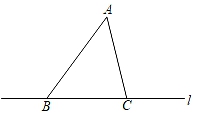 17. 如图,有一个含有30°角的直角三角板,一顶点放在直尺的一条边上,若∠2=65°,则∠1的度数是 .
17. 如图,有一个含有30°角的直角三角板,一顶点放在直尺的一条边上,若∠2=65°,则∠1的度数是 .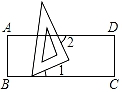 18. 某文具店“六一”期间开展促销活动,销售总价y与卖出笔记本数量x的关系如下表:
18. 某文具店“六一”期间开展促销活动,销售总价y与卖出笔记本数量x的关系如下表:数量x(件)
1
2
3
4
5
…
销售总价y(元)
8
14
20
26
32
…
则售价y与数量x之间的关系式是 .
三、解答题(本大题共6个题,满分66分)
-
19. 利用简便方法计算:(1)、(﹣2x5+3x3﹣ x2)÷(﹣ x)2;(2)、(﹣4)2021×(﹣0.25)2020+(﹣ )﹣1÷(3.14﹣π)0;(3)、(3a+2)2(3a﹣2)2﹣(﹣a+4)2 .20. 已知:|a2+b2﹣8|与(a﹣b﹣1)2互为相反数.(1)、求ab的值;(2)、先化简,再求值:(2a﹣b+1)(2a﹣b﹣1)﹣(a+2b)(a﹣b).21. 光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面AB与水杯下沿CD平行,光线EF从水中射向空气时发生折射,光线变成FH,点G在射线EF上,已知∠HFB=20°,∠FED=45°,求∠GFH的度数.
 22. 如图,直线 分别与直线 , 交于点E,F. 平分 , 平分 ,且 ∥ .求证: ∥ .
22. 如图,直线 分别与直线 , 交于点E,F. 平分 , 平分 ,且 ∥ .求证: ∥ .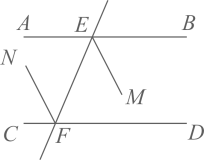 23. 如图,已知AB∥CD,点M为平面内一点,AM⊥DM于点M.过点M作MG⊥AB于点G,延长GM交CD于N,请说明∠AMG=∠MDC.
23. 如图,已知AB∥CD,点M为平面内一点,AM⊥DM于点M.过点M作MG⊥AB于点G,延长GM交CD于N,请说明∠AMG=∠MDC. 24. 在地球某地,地表以下岩层的温度y(℃)与所处深度x(km)之间的关系可以近似地用表达式y=35x+20来表示.(1)、这个问题中的自变量和因变量分别是什么?(2)、请用表格表示,在1﹣6km深度之间,该地表以下岩层的温度y与所处深度x之间的关系;
24. 在地球某地,地表以下岩层的温度y(℃)与所处深度x(km)之间的关系可以近似地用表达式y=35x+20来表示.(1)、这个问题中的自变量和因变量分别是什么?(2)、请用表格表示,在1﹣6km深度之间,该地表以下岩层的温度y与所处深度x之间的关系;深度/km
1
2
3
4
5
6
温度℃
(3)、当深度x每增加1km时,地表以下岩层的温度y的变化情况怎样?25. 促进青少年健康成长是实施“健康中国”战略的重要内容.为了引导学生积极参与体育运动,某校举办了一分钟跳绳比赛,随机抽取了40名学生一分钟跳绳的次数进行调查统计,并根据调查统计结果绘制了表格和统计图.
请结合上述信息完成下列问题:
(1)、a= , b= .(2)、请补全频数分布直方图.(3)、在扇形统计图中,“良好”等级对应的圆心角的度数是 .(4)、若该校有2000名学生,根据抽样调查结果,请估计该校学生一分钟跳绳次数达到合格及以上的人数.四、附加题(本大题共2个题,满分30分)
-
26. 数学是研究现实世界的数量关系与空间形式的科学,同学们,下面我们就用数形结合思想来解决下面问题吧!(1)、将图①甲中阴影部分的小长方形变换到图乙位置,你根据两个图形的面积关系得到的数学公式是 .
 (2)、将图②甲中阴影部分的一个小长方形变换到图乙位置,你根据两个图形的面积关系写出一个等式:(a﹣b)()=a2+ab﹣ .
(2)、将图②甲中阴影部分的一个小长方形变换到图乙位置,你根据两个图形的面积关系写出一个等式:(a﹣b)()=a2+ab﹣ . (3)、若把(2)中你写出的等式当做公式用,计算:(x﹣y)[(x+2y)4÷(x+2y)3];(4)、图③甲是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图③乙那样拼成一个正方形,则图③乙中间空余的部分的面积是 .
(3)、若把(2)中你写出的等式当做公式用,计算:(x﹣y)[(x+2y)4÷(x+2y)3];(4)、图③甲是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图③乙那样拼成一个正方形,则图③乙中间空余的部分的面积是 . (5)、观察图③乙,请你写出三个代数式(a+b)2(a﹣b)2 , ab之间的等量关系是 . 根据(5)中等量关系解决如下问题:若m+n=﹣7,mn=3.25,求m﹣n的值.27. 甲、乙两车早上从A城车站出发匀速前往B城车站,在整个行程中,两车离开A城的距离s与时间t的对应关系如图所示.
(5)、观察图③乙,请你写出三个代数式(a+b)2(a﹣b)2 , ab之间的等量关系是 . 根据(5)中等量关系解决如下问题:若m+n=﹣7,mn=3.25,求m﹣n的值.27. 甲、乙两车早上从A城车站出发匀速前往B城车站,在整个行程中,两车离开A城的距离s与时间t的对应关系如图所示. (1)、A,B两城之间距离是多少?(2)、求甲、乙两车的速度分别是多少?(3)、乙车出发多长时间追上甲车?(4)、从乙车出发后到甲车到达B城车站这一时间段,在何时间点两车相距40km?
(1)、A,B两城之间距离是多少?(2)、求甲、乙两车的速度分别是多少?(3)、乙车出发多长时间追上甲车?(4)、从乙车出发后到甲车到达B城车站这一时间段,在何时间点两车相距40km?