山东省济南市莱芜区2020-2021学年六年级下学期数学期末试卷（五四学制）
试卷更新日期：2021-11-05 类型：期末考试
一、选择题（共12个小题，每小题4分，共48分）
-
1. 下列运算正确的是（ ）。A、x3÷x2＝x B、x2•x3＝x6 C、x2+x2＝x4 D、（2x2）3＝6x62. 下列调查中，最适合采用普查的调查方式的是（ ）。A、调查本地区市民平均每日废弃口罩的数量 B、调查某批次LED灯泡的使用寿命 C、调查“嫦娥五号”月球探测器零部件的合格情况 D、调查本地区市民进行垃圾分类的情况3. 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片，该芯片的制造工艺达到了0.000000022米.用科学记数法表示0.000000022为（ ）A、22×10﹣10 B、2.2×10﹣10 C、2.2×10﹣9 D、2.2×10﹣84. 下列说法正确的是（ ）。A、延长射线AB到C B、若AM＝BM，则M是线段AB的中点 C、两点确定一条直线 D、过三点能作且只能作一条直线5. 下列多项式乘法中，不能用平方差公式计算的是（ ）。A、（﹣x﹣y）（x﹣y） B、（﹣x+y）（x﹣y） C、（﹣x﹣y）（﹣x+y） D、（x+y）（﹣x+y）6. 如图，直线AB、CD相交于点O，OE平分∠AOD，若∠1＝38°，则∠COE等于（ ）。
A、66° B、76° C、109° D、144°7. 计算：0.252020×（﹣4）2021＝（ ）。A、﹣4 B、﹣1 C、1 D、48. 如图，已知D是线段AB中点，延长线段AB至C使BC＝AB，则下列结论中①AB＝2AD；②AC＝2BC；③AD＝BD＝ AC；④BC＝ AC；⑤BD＝ BC；⑥AC＝4BD，正确的有（ ）。
A、①③④⑥ B、①②⑤⑥ C、①②③④ D、②③⑤⑥9. 如图，将直尺与30°角的三角尺叠放在一起，若∠1＝40°，则∠2的大小是（ ）
A、40° B、60° C、70° D、80°10. 若﹣1＜x＜0，则x﹣1 ， x，x2的大小关系是（ ）。A、x2＜x﹣1＜x B、x﹣1＜x＜x2 C、x2＜x＜x﹣1 D、x＜x﹣1＜x211. 甲、乙两人利用不同的交通工具，沿同一路线从A地出发前往B地，甲先出发，两人行驶的路程y（km）与甲出发的时间x（h）之间的关系如图所示，根据图象得到如下结论，其中错误的是（ ）。
A、甲的速度是40km/h B、乙出发3小时追上甲 C、乙比甲早1小时到达 D、乙在AB的中点处追上甲12. 如图，两个正方形的边长分别为a、b，如果a、b满足a+b＝6，ab＝8，则阴影部分的面积为（ ）。
A、14 B、12 C、9 D、6二、填空题（本大题共6个小题，每小题4分，共24分。）
-
13. 高速公路的建设带动我国经济的快速发展．在高速公路的建设中，通常要从大山中开挖隧道穿过，把道路取直，以缩短路程．这样做蕴含的数学道理是。14. 如果（x﹣1）（x+2）＝x2+mx+n，则m+n＝。15. 如图，将一副三角板的两个直角顶点重合摆放到桌面上，若∠BOC＝34°27'，则∠AOD＝。
16. 计算：（3x2y）2•（﹣15xy3）÷（﹣9x4y2）＝。17. 已知∠AOB＝50°，OC平分∠AOB，∠BOD＝15°，则∠COD＝度。18. 小颖准备乘出租车到距家超过3km的莱芜图书馆参观，出租车的收费标准如下：里程数/km
收费/元
3km以内（含3km）
7.00
3km以外每增加1km
1.50
则小颖应付车费y（元）与行驶里程数x（x＞3）之间的关系式为。
三、解答题（本大题共9小题，共78分。）
-
19. 计算：|﹣3|﹣（4﹣π）0+（﹣ ）﹣1﹣（﹣1）2021 ．20. 先化简，再求值：[y（2x﹣y）﹣（x+y）（x﹣y）]÷（﹣x），其中x＝﹣2，y＝﹣ ．21. 如图，已知OD平分∠AOB，射线OC在∠AOD内，∠BOC＝2∠AOC，∠AOB＝120°，求∠COD的度数．
22. 如图，已知点C、D在线段AB上，点D是AB中点，AC＝ AB，CD＝2．求线段AB长．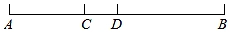
23. 如图，某公园有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，规划部门计划将阴影部分进行绿化，中间修建一座雕像，其底座是边长为（a+b）米的正方形．求绿化的面积是多少平方米？并求出当a＝3，b＝2时的绿化面积．
24. 为了解学生“最喜欢的出行方式”的情况，从全校学生中随机抽取部分学生进行调查，并根据调查统计结果绘制了统计图．
根据以上信息，解答下列问题：
(1)、求被调查的学生总人数；(2)、求出被调查的学生中，乘车的有多少人？并补全条形统计图；(3)、求“骑车”部分所对应的圆心角的度数；(4)、如果全年级共有1200名学生，请估计乘车的学生人数．25. 如图，AF的延长线与BC的延长线交于点E，AD∥BE，∠1＝∠2＝30°，∠3＝∠4＝80°．
(1)、求∠CAE的度数；(2)、AB与DC平行吗？为什么？26. 小王骑自行车匀速从甲地到乙地，在途中休息了一段时间后，仍按原速行驶．他距乙地的距离y（千米）与时间x（小时）的关系如图中折线所示，小李开车匀速从乙地到甲地，比小王晚出发一段时间，他距乙地的距离y（千米）与时间x（小时）的关系如图中线段AB所示．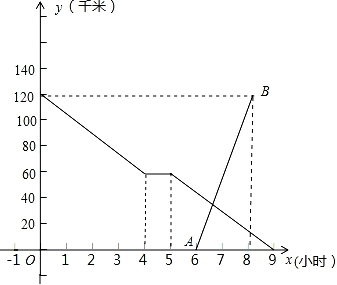
(1)、甲地到乙地的距离是千米，小王途中休息了小时；(2)、求小王骑自行车的速度，小李开车的速度；(3)、求小王出发几小时与小李相遇？27. 已知：如图1，直线AB、CD被直线MN所截，且AB∥CD．点E在直线AB、CD之间的线段MN上，P、Q分别在直线AB、CD上，连接PE、EQ．
(1)、小明探究发现：∠PEQ＝∠APE+∠CQE，请你帮小明说明理由；(2)、如图2，已知∠FPB＝ ∠EPB，∠FQD＝ ∠EQD，若∠PEQ＝80°，请你利用小明发现的结论求∠PFQ的度数；(3)、如图3，若∠FPB＝ ∠EPB，∠FQD＝ ∠EQD，请你直接写出∠PEQ和∠PFQ之间的数量关系．