辽宁省辽东南协作体2021-2022学年高二上学期数学第一次月考试卷
试卷更新日期:2021-11-04 类型:月考试卷
一、单选题
-
1. 若数组 ,1, 和 , , 满足 ,则实数 等于( )A、-3 B、-2 C、 D、2. 若 , , ,则 等于( )A、 B、 C、 D、3. 若直线 的方向向量为 ,平面 的法向量为 ,则( )A、 B、 C、 D、 与 斜交4. 已知正四面体 的棱长为1,且 ,则 ( )A、 B、 C、 D、5. 已知向量 ,且 与 平行,则 的值是( )A、 B、 C、-3 D、36. 笛卡尔是世界著名的数学家,他因将几何坐标体系公式化而被认为是解析几何之父.据说在他生病卧床时,还在反复思考一个问题:通过什么样的方法,才能把“点”和“数”联系起来呢?突然,他看见屋顶角上有一只蜘蛛正在拉丝织网,受其启发建立了笛卡尔坐标系的雏形.在如图所示的空间直角坐标系中,单位正方体顶点 关于 轴对称的点的坐标是( )
 A、 B、 C、 D、7. 已知四面体 各棱长为 , 是棱 的中点,则异面直线 与 所成角的余弦值( )A、 B、 C、 D、8. 在三棱锥 中, 底面ABC, , , ,则点C到平面PAB的距离是A、 B、 C、 D、
A、 B、 C、 D、7. 已知四面体 各棱长为 , 是棱 的中点,则异面直线 与 所成角的余弦值( )A、 B、 C、 D、8. 在三棱锥 中, 底面ABC, , , ,则点C到平面PAB的距离是A、 B、 C、 D、二、多选题
-
9. 在正方体 中,E、F、G、H分别为 、 、 、 的中点,则下列结论中正确的是( )A、 B、 平面 C、 D、10. 已知点P是平行四边形 所在的平面外一点,如果 , , .对于结论:① ;② ;③ 是平面 的法向量;④ .其中正确的是( )A、① B、② C、③ D、④11. 在以下命题中,不正确的命题有( )A、 是 共线的充要条件 B、若 ,则存在唯一的实数 ,使 C、对空间任意一点 和不共线的三点A,B,C,若 ,则P,A,B,C四点共面 D、若 为空间的一个基底,则 构成空间的另一个基底12. 将正方形 沿对角线 折成直二面角 ,有如下四个结论:① ;② 是等边三角形;③ 与平面 所成的角为 ;④ 与 所成的角为 .其中正确的结论有( )A、① B、② C、③ D、④
三、填空题
-
13. 已知平面 和平面 的法向量分别为 , ,若 ,则 ;14. 在直三棱柱 中,以下向量可以作为平面 法向量的是 . (填序号)
① ;② ;③ ;④ .
15. 已知 ,若 三向量共面,则 .16. 在三棱锥 中,已知 , , ,则四、解答题
-
17. 如图,在四棱锥 中,底面 是边长为 的正方形,侧棱 的长为2,且 与 、 的夹角都等于60°, 是 的中点,设 , , .
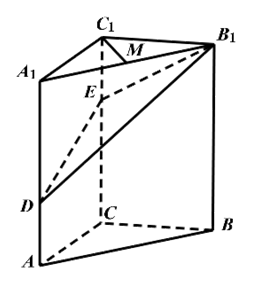
 (1)、试用 , , 表示向量 ;(2)、求 的长.18. 已知向量 =(1,-3,2), =(-2,1,1),点A(-3,-1,4),B(-2,-2,2).(1)、求|2 + |;(2)、在直线AB上,是否存在一点E,使得 ⊥ ?(O为原点)19. 如图,在直三棱柱ABCA1B1C1中,∠ABC= ,D是棱AC的中点,且AB=BC=BB1=2.
(1)、试用 , , 表示向量 ;(2)、求 的长.18. 已知向量 =(1,-3,2), =(-2,1,1),点A(-3,-1,4),B(-2,-2,2).(1)、求|2 + |;(2)、在直线AB上,是否存在一点E,使得 ⊥ ?(O为原点)19. 如图,在直三棱柱ABCA1B1C1中,∠ABC= ,D是棱AC的中点,且AB=BC=BB1=2. (1)、求证:AB1∥平面BC1D;(2)、求异面直线AB1与BC1的夹角.
(1)、求证:AB1∥平面BC1D;(2)、求异面直线AB1与BC1的夹角.