初中数学苏科版九年级上学期期中复习专题6 直线与圆的位置关系和切线的性质与判定
试卷更新日期：2021-11-03 类型：复习试卷
一、单选题
-
1. 已知⊙O的直径为4，点O到直线m的距离为2，则直线m与⊙O的位置关系是（ ）A、相交 B、相切 C、相离 D、无法判断2. 在平面直角坐标系中，以点 为圆心，1为半径的圆与 轴的位置关系是（ ）A、相离 B、相切 C、相交 D、不确定3. 已知⊙O的半径r=2，圆心O到直线l的距离d是方程x2﹣5x+6=0的解，则直线l与⊙O的位置关系是（ ）A、相切 B、相交 C、相切或相交 D、相切或相离4. 如图，两个同心圆，大圆的半径为5，小圆的半径为3，若大圆的弦AB与小圆有公共点，则弦AB的取值范围是（ ）
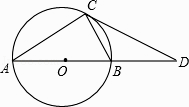
A、8≤AB≤10 B、8＜AB≤10 C、4≤AB≤5 D、4＜AB≤55.如图，AB是⊙O的弦，AO的延长线交过点B的⊙O的切线于点C，如果∠ABO=20°，则∠C的度数是（ ）
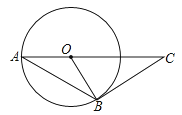A、70° B、50° C、45° D、20°6. 如图， 是 的弦，点 在过点 的切线上， ， 交 于点 .若 ，则 的度数等于（ ）
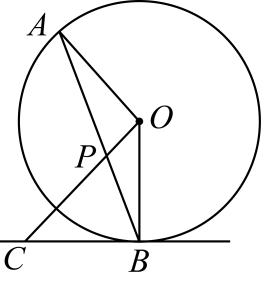A、 B、 C、 D、7. 下列命题中的假命题是（ ）A、和圆有唯一公共点的直线是圆的切线 B、切线垂直于过切点的半径 C、在同圆或等圆中，等弦所对的圆心角相等 D、平分弦的直径垂直于弦，并且平分弦所对的两条弧8. 如图，BC是⊙O的直径，AD是⊙O的切线，切点为D，AD与CB的延长线交于点A，∠C=30°，给出下面四个结论：①AD=DC；②AB=BD；③AB= BC；④BD=CD，
其中正确的个数为（ ）
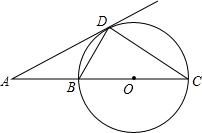A、4个 B、3个 C、2个 D、1个9. 如图，小敏家厨房一墙角处有一自来水管，装修时为了美观，准备用木板从AB处将水管密封起来，互相垂直的两墙面与水管分别相切于D，E两点，经测量AD=10cm，BE=15cm，则该自来水管的半径为（ ）cm．
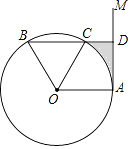
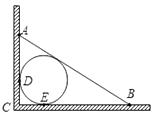A、5 B、10 C、6 D、810. 如图，在边长为2的正方形 中， 是以 为直径的半圆的切线，则图中阴影部分的面积为（ ）
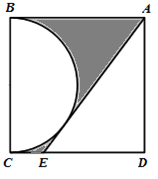A、 B、 C、1 D、二、填空题
-
11. 已知⊙O的直径等于12cm，圆心O到直线l的距离为5cm，则直线l与⊙O的交点个数为 ．12. 已知⊙O的半径为5cm，点O到直线 的距离为d，
当d=4cm时，直线 与⊙O；
当d=时，直线 与⊙O相切；
当d=6 cm时，直线 与⊙O ．
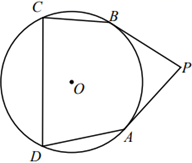
13. 已知直线y=kx（k≠0）经过点（12，﹣5），将直线向上平移m（m＞0）个单位，若平移后得到的直线与半径为6的⊙O相交（点O为坐标原点），则m的取值范围为 ．14. 如图，PA，PB是⊙O的切线，A，B为切点，∠OAB=38°，则∠P=°.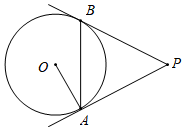
15. 如图，PA、PB是 的切线，A、B为切点，点C、D在⊙O上.若∠P＝102°，则∠A＋∠C＝°.
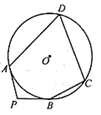16. 如图，⊙O切△ABC的BC于D，切AB、AC的延长线于E、F，△ABC的周长为18，则AE＝.
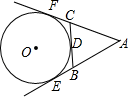17. 如图，☉O是△ABC的内切圆，与边BC，CA，AB的切点分别为D，E，F，若∠A=70°，则∠EDF=.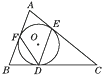
三、综合题
-
18. 如图，PA、PB是⊙O的切线，A、B为切点，连接AO并延长，交PB的延长线于点C，连接PO，交⊙O于点D.
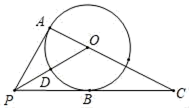(1)、求证：∠APO＝∠CPO；(2)、若⊙O的半径为3，OP＝6，∠C＝30°，求PC的长.
