甘肃省临洮县2021-2022学年八年级上学期数学期中考试试卷
试卷更新日期：2021-11-03 类型：期中考试
一、选择题：（本大题共10小题，每题3分，共30分。）
-
1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 一个三角形的三边长分别为a，b，c，则a，b，c的值不可能是（ ）A、3，4，5 B、5，7，7 C、10，6，4.5 D、4，5，93. 如图，小强利用全等三角形的知识测量池塘两端M，N的距离，如果△PQO≌△NMO，则只需测出其长度的线段是（ ）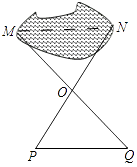
A、PO B、PQ C、MO D、MQ4. 设四边形的内角和等于a，六边形的外角和等于b，则a与b的关系是（ ）A、a＞b B、a＜b C、a=b D、B=a+360°5. 如图，将直角三角尺的直角顶点靠在直尺上，且斜边与这根直尺平行，那么在形成的这个图中与∠α互余的角共有（ ）
A、1个 B、2个 C、3个 D、4个6.如图，某同学把一块三角形的玻璃打碎成三片，现在他要到玻璃店去配一块完全一样形状的玻璃．那么最省事的办法是带（ ）
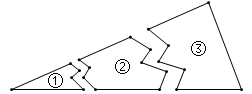A、带①去 B、带②去 C、带③去 D、带①②去7. 如图，在△ABC中，AB=AC=20cm，DE垂直平分AB，垂足为E，交AC于D，若△DBC的周长为35cm，则BC的长为（ ）
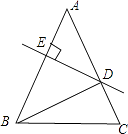A、5cm B、10cm C、15cm D、17.5cm8. 如图，一艘海轮位于灯塔P的南偏东70°方向的M处，它以每小时40海里的速度向正北方向航行，2小时后到达位于灯塔P的北偏东40°的N处，则N处与灯塔P的距离为（ ）
A、40海里 B、60海里 C、70海里 D、80海里9. 如图，在△ABC中，AB=AC，∠A=30°，以B为圆心，BC的长为半径画弧，交AC于点D，连接BD，则∠ABD=（ ）
A、30° B、45° C、60° D、90°10. 如图，∠ABC，∠ACB的平分线相交于点F，过点F作DE∥BC，交AB于D，交AC于E，那么下列结论正确的是：①△BDF，△CEF都是等腰三角形；②DE=BD＋CE；③△ADE的周长为AB＋AC；④BD=CE.（ ）
A、③④ B、①②③ C、①② D、②③④二、 填空题（本大题共8小题，每小题3分，共24分。）
-
11. 一木工师傅现有两根木条，木条的长分别为40 cm和30 cm，他要选择第三根木条，将它们钉成一个三角形木架.设第三根木条长为x cm，则x的取值范围是.12. 点P（1，﹣2）关于y轴对称的点的坐标为 ．13. 等腰三角形的周长为14，其一边长为4，那么，它的底边为.14. 如图，正方形ABCD中，截去∠A，∠C后，∠1，∠2，∠3，∠4的和为 ．
15. 如图，点B、F、C、E在一条直线上，已知FB=CE，AC∥DF，请你添加一个适当的条件使得△ABC≌△DEF．
16. 如图，已知PA⊥ON于A，PB⊥OM于B，且PA=PB，∠MON=50°，∠OPC=30°，则∠PCA=.
17. 如图，在Rt△ABC中，∠B=90°，AB=3 cm，S△ABC=6 cm2 ， 将△ABC折叠，使点C与点A重合，得折痕DE，则△ABE的周长等于 cm.
18. 当三角形中一个内角α是另一个内角β的一半时，我们称此三角形为“半角三角形”，其中α称为“半角”．如果一个“半角三角形”的“半角”为20°，那么这个“半角三角形”的最大内角的度数为 ．三、解答题（一）（19题4分，20题6分，21题5分，22题7分，23题7分，共29分）
-
19. 如图，AD⊥BC，∠1=∠B，∠C=65°，求∠BAC的度数
20. 如图，△ABC是等腰三角形，AB=AC，∠A=36°．
(1)、尺规作图：作∠B的角平分线BD，交AC于点D（保留作图痕迹，不写作法）；(2)、判断△DBC是否为等腰三角形，并说明理由．21. 如图，点B、E、C、F在同一条直线上，AB=DE，AC=DF，BE=CF，求证：AB∥DE．
22. 如图，在平面直角坐标系xOy中，A（1，2），B（3，1），C（﹣2，﹣1）．
(1)、在图中作出△ABC关于x轴的对称图形△A1B1C1 ．(2)、写出点A1 ， B1 ， C1的坐标（直接写答案）A1 B1 C1
(3)、求△ABC的面积．23. 如图，在△ABC中， ∠ACB=90°，AC=BC，直线MN经过点C， AD⊥MN于点D， BE ⊥MN于点E，
求证：
(1)、△ADC≌△CEB；(2)、DE=AD+BE四、解答题（二）（24、25每小题各6分，26题8分，27题8分、28题9分，共37分）
-
24.
如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D．
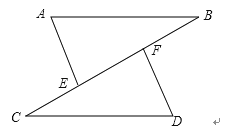(1)、求证：AB=CD．(2)、若AB=CF，∠B=30°，求∠D的度数．25. 如图，AB=CD， BF⊥AC， DE⊥AC， AE=CF.求证：BD平分EF.
26. 如图，BD是∠ABC的平分线，AB＝BC，点E在BD上，连接AE，CE，DF⊥AE，DG⊥CE，垂足分别是F，G.
(1)、求证：△ABE≌△CBE；(2)、求证：DF＝DG.27.如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．
求证：
(1)、FC＝AD
(2)、AB＝BC＋AD．
28. AB和AC 相交于点A，BD和CD相交于点D，探究∠BDC与∠B 、 ∠C、∠BAC的关系
小明是这样做的：
解：如图（2）以点A为端点作射线AD
∵∠1是△ABD的外角
∴∠1= ∠B+∠BAD
同理∠2=∠C+∠CAD
∴∠1+∠2=∠B+∠BAD+∠C+∠CAD
即∠BDC=∠B+∠C+∠BAC
小英的思路是：如图（3）延长BD交AC于点E.
(1)、按小英的思路完成∠BDC=∠B+∠C+∠BAC这一结论.(2)、如图：△ABC中，BO、CO分别是∠ABC与∠ACB的角平分线，且BO、CO相交于点O.猜想∠BOC与∠A有怎样的关系，并加以证明.