湖北省襄阳市谷城县石花镇2021-2022学年九年级上学期数学期中考试试卷

试卷更新日期：2021-11-03 类型：期中考试

进入出卷网下载

一、选择题：（本大题共10个小题，每小题3分，共30分．）

1. 下列四个图形中，既是轴对称图形又是中心对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 关于x的方程(m+1)x²+2mx-3=0是一元二次方程，则m的取值是（）

A、任意实数 B、m≠1 C、m≠-1 D、m>-1

查看试题解析
3. 若x=-2是关于x的一元二次方程 $x^{2} + \frac{3}{2} a x - a^{2} = 0$ 的一个根，则a的值为（）

A、﹣1或4 B、﹣1或﹣4 C、1或﹣4 D、1或4

查看试题解析
4. 一元二次方程x²﹣4x+4=0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
5. 若关于x的一元二次方程方程（k﹣1）x²+4x+1=0有两个不相等的实数根，则k的取值范围是（　　）

A、k＜5 B、k＜5，且k≠1 C、k≤5，且k≠1 D、k＞5

查看试题解析
6. 若二次函数y=x²+mx的对称轴是x=3，则关于x的方程x²+mx=7的解为（　　）

A、x₁=0，x₂=6 B、x₁=1，x₂=7 C、x₁=1，x₂=﹣7 D、x₁=﹣1，x₂=7

查看试题解析
7. 将抛物线y=x²﹣2x+3向上平移2个单位长度，再向右平移3个单位长度后，得到的抛物线的解析式为（）

A、y=（x﹣1）²+4 B、y=（x﹣4）²+4 C、y=（x+2）²+6 D、y=（x﹣4）²+6

查看试题解析
8.
如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A（﹣2，5）的对应点A′的坐标是（　　）

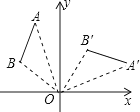A、（2，5） B、（5，2） C、（2，﹣5） D、（5，﹣2）

查看试题解析
9. 当a-1≤x≤a时，函数y=x²-2x+1的最小值为1，则a的值为（）

A、1 B、2 C、1或2 D、0或3

查看试题解析
10. 如图，在Rt△ABC中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：①△AED≌△AEF；②△ABE≌△ACD；③BE+DC=DE；④ $B E^{2} + D C^{2} = D E^{2}$ 其中正确的是（）

A、②④ B、①④ C、②③ D、①③

查看试题解析

二、填空题：（本大题共6个小题，每小题3分，共18分．）

11. 方程x（x-3)=2(x-3)的解为.

查看试题解析
12. 有一人患了流感，经过两轮传染后共有100人患了流感，那么每轮传染中平均一个人传染的人数为人.

查看试题解析
13. 若点M（a+1，2b-3）与点N（2a+1，-b-1）关于原点中心对称，则a+b=.

查看试题解析
14. 如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为.

查看试题解析
15. 如图，有一抛物线拱桥，当水位线在AB位置时，拱顶离水面2m，水面宽4m，当水面下降1m后，水面宽为m.

查看试题解析
16. 关于x的函数 $y = a x^{2} - 2 x + 1$ 与x轴有唯一交点，则a的值是.

查看试题解析

三、解答题：(本大题共9个小题，共72分．)

17. 解方程：

(1)、 $\frac{1}{2} {(2 x - 5)}^{2} - 2 = 0$ ；

(2)、4(x-2)²=(x+5)²；

(3)、3x(x-1)=2-2x

查看试题解析
18. 若关于x的一元二次方程x²-3x+m=0有实数根，

(1)、求实数m的取值范围；

(2)、若等腰三角形的一边长为1，另两边长是方程的根，求等腰三角形的周长.

查看试题解析
19. 已知函数 $y = {(x + 1)}^{2} - 4$

(1)、若图象与x轴的交点为A、B，与y轴的交点C，求△ABC的面积；

(2)、直接回答：①当x取何值时，函数值大于0？②当x取何值时，函数值y随x的增大而增大？

查看试题解析
20. 新农村建设有效促进了乡村旅游业的发展．某镇2018年实现旅游收入1500万元，到2020年该项收入达到2160万元，且从2018年到2020年，每年旅游收入的年增长率相同．

(1)、该旅游收入的年增长率；

(2)、若该镇旅游收入的年增长率保持不变，预计2021年旅游收入达到多少万元？

查看试题解析
21. 某项绿化工程中有一块长为20米，宽为8米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为56米² ，两块绿地之间及周边留有宽度相等的人行通道（如图所示），问人行通道的宽度是多少米？

查看试题解析
22. 如图，P是正三角形ABC内的一点，且PA＝6，PB＝8，PC＝10，若将△PAC绕点A逆时针旋转后，得到△P′AB，求点P与点P′之间的距离及∠APB的度数．

查看试题解析
23. 为了落实国务院“三农”优惠政策，最近，市委市政府出台了一系列优惠措施，使农民收入大幅度增加.某农户生产经销一种农副产品，已知这种产品的成本价为20元/千克.市场调查发现，该产品每天的销售量ｗ(千克)与销售价x(元/千克)有如下关系：w=-2x+80.设这种产品每天的销售利润为y(元).

(1)、求y与x之间的函数关系式.

(2)、当销售价定为多少元时，每天的销售利润最大?最大利润是多少?

(3)、如果物价部门规定这种产品的销售价不得高于28元/千克，该农户想要每天获得150元的销售利润，销售价应定为多少元?

查看试题解析
24. 已知△ABC是等边三角形．

(1)、将△ABC绕点A逆时针旋转角θ（0°＜θ＜180°），得到△ADE，BD和EC所在直线相交于点O．
①如图a，当θ=20°时，△ABD与△ACE是否全等？ ▲ （填“是”或“否”），∠BOE= ▲ 度；

②当△ABC旋转到如图b所在位置时，求∠BOE的度数；

(2)、如图c，在AB和AC上分别截取点B′和C′，使AB′=AC′，连接B′C′，将△AB′C′绕点A逆时针旋转角（0°＜θ＜180°），得到△ADE，BD和EC所在直线相交于点O，请利用图c探索∠BOE的度数，直接写出结果，不必说明理由．

查看试题解析
25. 如图，抛物线 $y = - \frac{1}{2} x^{2} + b x + c$ 与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．

(1)、求抛物线的表达式；

(2)、在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；

(3)、点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．

查看试题解析