重庆市江津二中等十一校2021年数学中考一模联考试卷

试卷更新日期：2021-11-03 类型：中考模拟

进入出卷网下载

一、单选题

1. 在-2，0，3， $\sqrt{6}$ 这四个数中，最大的数是（）

A、-2 B、0 C、3 D、 $\sqrt{6}$

查看试题解析
2. 下列调查中，最适宜采用普查方式的是（）

A、对我国初中学生视力状况的调查 B、对量子科学通信卫星上某种零部件的调查 C、对一批节能灯管使用寿命的调查 D、对“最强大脑”节目收视率的调查

查看试题解析
3. 随着我国经济快速发展，轿车进入百姓家庭，小明同学在街头观察出下列四种汽车标志，其中既是中心对称图形，又是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
4. 下列运算错误的是（）

A、 ${(a^{- 2})}^{3} = a^{- 6}$ B、 ${(a^{2})}^{3} = a^{5}$ C、 $a^{2} \div a^{3} = a^{- 1}$ D、 $a^{2} \cdot a^{3} = a^{5}$

查看试题解析
5. 如图，圆O是Rt△ABC的外接圆，∠ACB=90°，∠A=25°，过点C作圆O的切线，交AB的延长线于点D，则∠D的度数是（）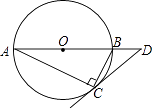

A、25° B、40° C、50° D、65°

查看试题解析
6. 如图是由五个相同的小正方体搭成的几何体，则它的主视图是（）

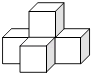A、 B、 C、 D、

查看试题解析
7. 用一个圆心角为120°，半径为3的扇形作一个圆锥的侧面，则这个圆锥的底面半径为（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{3}{2}$ D、2

查看试题解析
8. 某商场一月份的营业额为400万元，第一季度营业总额为1600万元，若平均每月增长率为x，则可列方程为（　　）

A、400（1+x）²=1600 B、400[1+（1+x）+（1+x）²]=1600 C、400+400x+400x²=1600 D、400（1+x+2x）=1600

查看试题解析
9. 如图，用相同的小正方形按照某种规律进行摆放，则第8个图形中小正方形的个数是（）

A、71 B、78 C、85 D、89

查看试题解析
10. 若关于x的方程 $\frac{a x}{x - 2}$ = $\frac{4}{x - 2}$ +1无解，则a的值为（）

A、1 B、2 C、1或2 D、0或2

查看试题解析
11. 已知△ABC，D，E分别在AB，AC边上，且DE∥BC，AD=2，DB=3，△ADE面积是4则四边形DBCE的面积是（）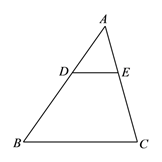

A、6 B、9 C、21 D、25

查看试题解析
12. 甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶 $2 h$ ，并且甲车途中休息了 $0.5 h$ ，如图是甲、乙两车行驶的距离 $y (km)$ 与时间 $x (h)$ 的函数图象，有以下结论：
① $m = 1$ ；② $a = 40$ ；③甲车从A地到B地共用了7小时；④当两车相距 $50 km$ 时，乙车用时为 $\frac{1}{4} h$ .其中正确结论的个数是（）.

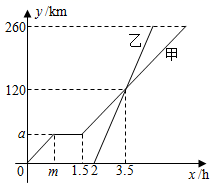A、4 B、3 C、2 D、1

查看试题解析

二、填空题

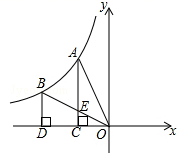
13. 已知1纳米=0.000000001米，用科学记数法表示1纳米=米.

查看试题解析
14. 4的算术平方根是．

查看试题解析
15. 从0到9这10个自然数中随机取一个数，能使 $\frac{x}{\sqrt{3 - x}}$ 有意义的概率是.

查看试题解析
16. 直角三角形的两边分别是6和8，则第三边等于.

查看试题解析
17. 如图，反比例函数 $y = \frac{k}{x}$ （k≠0）的图象经过A，B两点，过点A作AC⊥x轴，垂足为C，过点B作BD⊥x轴，垂足为D，连接AO，连接BO交AC于点E，若OC=CD，四边形BDCE的面积为2，则k的值为.

查看试题解析
18. 如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点，抛物线的解析式为y=x²﹣6x﹣16，AB为半圆的直径，则这个“果圆”被y轴截得的线段CD的长为.

查看试题解析

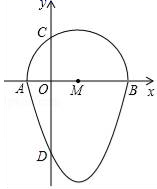
三、解答题

19.

(1)、计算： ${(\frac{1}{3})}^{- 2} - 2017^{0} + | 2 - 2 \sqrt{3} | - \tan 60 °$ ；

(2)、解方程组 ${\begin{array}{l} x + y = 1 \\ 4 x + y = - 8 \end{array}$ .

查看试题解析
20. 如图，矩形ABCD，E是AB上一点，且DE=AB，过C作CF⊥DE于F.

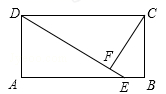(1)、猜想：AD与CF的大小关系；

(2)、请证明上面的结论.

查看试题解析
21. 如图， $△ A B 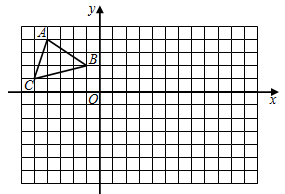C$ 各顶点坐标分别为： $A (- 4 ， 4)$ ， $B (- 1 ， 2)$ ， $C (- 5 ， 1)$ .

⑴画出 $△ A B C$ 关于原点O为中心对称的 $△ A_{1} B_{1} C_{1}$ ；

⑵将 $△ A_{1} B_{1} C_{1}$ 向上平移4个单位得到 $△ A_{2} B_{2} C_{2}$ ；画出图形并写出下列各点坐标 $A_{2}$ ：▲ ， $B_{2}$ ：▲ ， $C_{2}$ ：▲ ；

⑶观察图形，若 $△ A B C$ 中存在点 $P (m ， n)$ ，则在 $△ A_{2} B_{2} C_{2}$ 中对应点 $P_{2}$ 的坐标为：▲ .

查看试题解析
22. 2016年2月，某市首条绿道免费公共自行车租赁系统正式启用．市政府在2016年投资了112万元，建成40个公共自行车站点、配置720辆公共自行车．今后将逐年增加投资，用于建设新站点、配置公共自行车．预计2018年将投资340.5万元，新建120个公共自行车站点、配置2205辆公共自行车．

(1)、请问每个站点的造价和公共自行车的单价分别是多少万元？

(2)、请你求出2016年到2018年市政府配置公共自行车数量的年平均增长率．

查看试题解析
23. 某中学需在短跑、长跑、跳远、跳高四类体育项目中各选拔一名同学参加市中学生运动会.根据平时成绩，把各项目进入复选的学生情况绘制成如下不完整的统计图：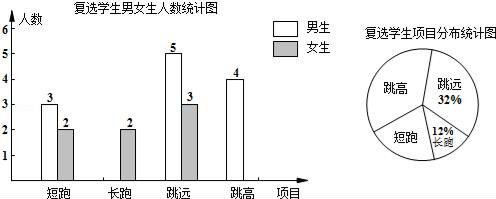

(1)、参加复选的学生总人数为人，扇形统计图中短跑项目所对应圆心角的度数为°；

(2)、补全条形统计图，并标明数据；

(3)、求在跳高项目中男生被选中的概率.

查看试题解析
24. 若实数a可以表示成两个连续自然数的倒数差，即a＝ $\frac{1}{n} - \frac{1}{n + 1}$ ，那么我们称a为第n个“1阶倒差数”，例如 $\frac{1}{2}$ ＝1- $\frac{1}{2}$ ，∴ $\frac{1}{2}$ 是第1个“1阶倒差数”， $\frac{1}{6}$ ＝ $\frac{1}{2}$ - $\frac{1}{3}$ ，∴ $\frac{1}{6}$ 是第2个“1阶倒差数”.同理，若b＝ $\frac{1}{n}$ - $\frac{1}{n + 2}$ ，那么，我们称b为第n个“2阶倒差数”.

(1)、判断 $\frac{1}{32}$ 是否为“1阶倒差数”；直接写出第5个“2阶倒差数”；

(2)、若c，d均是由两个连续奇数组成的“2阶倒差数”，且 $\frac{1}{d}$ $- \frac{1}{c}$ ＝22，求c，d的值.

查看试题解析
25. 如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F.

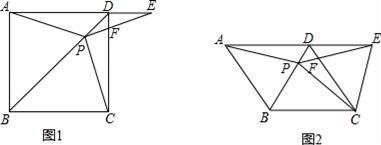(1)、求∠CPE的度数；

(2)、如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由.

查看试题解析
26. 如图，抛物线y=ax²+bx过A（4，0），B（1，3）两点，点C、B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H．

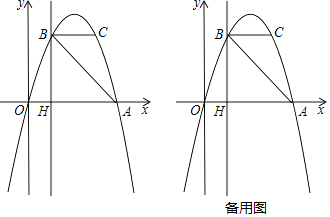(1)、求抛物线的表达式；

(2)、点P是抛物线上一动点，且位于第四象限，当△ABP的面积为6时，求出点P的坐标；

(3)、若点M在直线BH上运动，点N在x轴上运动，当以点C、M、N为顶点的三角形为等腰直角三角形时，请直接写出此时△CMN的面积．

查看试题解析