重庆市巴南区重点中学2021年指标到校考试数学试卷
试卷更新日期:2021-11-03 类型:中考模拟
一、单选题
-
1. 实数2021的相反数是( )A、2021 B、-2021 C、 D、2. 下列图形是某几届冬奥会图标,其中是轴对称图形,但不是中心对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 3. 下列命题中,是真命题的是( ).A、同旁内角互补 B、有两边及一角对应相等的两个三角形全等 C、矩形的对角线互相平分 D、多边形的内角和为4. “二十四节气”是中国古代劳动人民长期经验积累的结晶,它包括立春、惊蛰、春分、立夏等,同时,它与白昼时长密切相关.如图是一年中部分节气所对应的白昼时长示意图.在下列选项中白昼时长不足10小时的节气是( ).
3. 下列命题中,是真命题的是( ).A、同旁内角互补 B、有两边及一角对应相等的两个三角形全等 C、矩形的对角线互相平分 D、多边形的内角和为4. “二十四节气”是中国古代劳动人民长期经验积累的结晶,它包括立春、惊蛰、春分、立夏等,同时,它与白昼时长密切相关.如图是一年中部分节气所对应的白昼时长示意图.在下列选项中白昼时长不足10小时的节气是( ).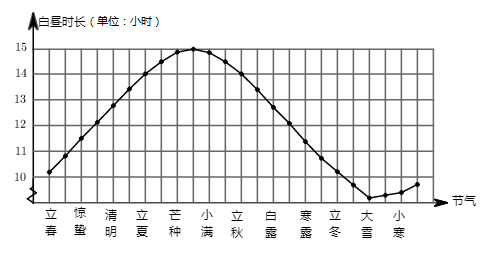 A、惊蛰 B、立夏 C、大雪 D、寒露5. 如图, 与 相切于点A, 交 于点B,点C在 上,连接 .若 ,则 的度数为( ).
A、惊蛰 B、立夏 C、大雪 D、寒露5. 如图, 与 相切于点A, 交 于点B,点C在 上,连接 .若 ,则 的度数为( ). A、 B、 C、 D、6. 下列计算中,正确的是( ).A、 B、 C、 D、7. 估计 的值应在( ).A、0到1之间 B、1到2之间 C、2到3之间 D、3到4之间8. 如图, 与 是位似图形,点O是位似中心,且 的面积为4.若 ,则 的面积为( ).
A、 B、 C、 D、6. 下列计算中,正确的是( ).A、 B、 C、 D、7. 估计 的值应在( ).A、0到1之间 B、1到2之间 C、2到3之间 D、3到4之间8. 如图, 与 是位似图形,点O是位似中心,且 的面积为4.若 ,则 的面积为( ). A、8 B、12 C、20 D、369. 把四边形和三角形按如图所示的规律拼图案,其中图案①中共有4个三角形,图案②中共有7个三角形,图案③中共有10个三角形,…,若按此规律拼图案,则图案⑧中共有( ).
A、8 B、12 C、20 D、369. 把四边形和三角形按如图所示的规律拼图案,其中图案①中共有4个三角形,图案②中共有7个三角形,图案③中共有10个三角形,…,若按此规律拼图案,则图案⑧中共有( ). A、13个三角形 B、19个三角形 C、25个三角形 D、31个三角形10. 如图,某同学在山坡坡脚A处时,测得一座楼房的楼顶B处的仰角为 ,沿山坡往上走到C处时,测得这座楼房的楼顶B处的仰角为 .已知 ,且 ,点O、A、C、B在同一平面内,若此山坡的坡度为 ,则这座楼房的高 的值是( )
A、13个三角形 B、19个三角形 C、25个三角形 D、31个三角形10. 如图,某同学在山坡坡脚A处时,测得一座楼房的楼顶B处的仰角为 ,沿山坡往上走到C处时,测得这座楼房的楼顶B处的仰角为 .已知 ,且 ,点O、A、C、B在同一平面内,若此山坡的坡度为 ,则这座楼房的高 的值是( ) A、 B、 C、 D、11. 从-3,-2,-1,0,1,2这六个数中,随机取出一个数,记为m,若m使关于x的函数 的图象与x轴有交点,且使关于x的不等式组 有解,则所有满足条件的m的绝对值的和是( ).A、7 B、5 C、-1 D、-512. 如图, 轴,垂足为C, 轴,垂足为A,反比例函数 的图象交矩形 的边 于点D,交边 与点E,且 .若四边形 的面积为24,则k的值为( ).
A、 B、 C、 D、11. 从-3,-2,-1,0,1,2这六个数中,随机取出一个数,记为m,若m使关于x的函数 的图象与x轴有交点,且使关于x的不等式组 有解,则所有满足条件的m的绝对值的和是( ).A、7 B、5 C、-1 D、-512. 如图, 轴,垂足为C, 轴,垂足为A,反比例函数 的图象交矩形 的边 于点D,交边 与点E,且 .若四边形 的面积为24,则k的值为( ). A、4 B、6 C、8 D、12
A、4 B、6 C、8 D、12二、填空题
-
13. 计算: .14. 据统计,我国累计接种新冠疫苗超过230000000剂次.其中的数据230000000用科学记数法表示为.15. 现将背面完全相同,正面分别标有数字0,1,2,5的4张卡片洗匀后,背面朝上,从中任取一张,将该卡片正面上的数字记为m,再从剩下的3张卡片中任取一张,将该卡片正面上的数字记为n,则数字m,n之和为奇数的概率为.16. 如图,在 中, .以点A为圆心, 长为半径画弧,与 的延长线交于点D,则图中阴影部分面积为.
 17. 如图,点E、F分别在矩形 的边 上, 与 相交于点N.已知 .若将矩形 沿 折叠后,点D恰好与点E重合,则 的面积为.
17. 如图,点E、F分别在矩形 的边 上, 与 相交于点N.已知 .若将矩形 沿 折叠后,点D恰好与点E重合,则 的面积为. 18. 某公司对A村、B村、C村进行了合作办企的投资,其投资总额是对C村投资额的 倍.随着国家对乡村振兴的高度重视,该公司调整了投资计划,在原投资总额的基础上再增加一部分投资,并按3:3:8的比例分别对A村、B村、C村增加投资.该公司调整投资计划后,若该公司对A村的投资总额与该公司对三个村的投资总额的和的比为6:13,且该公司对B村增加的投资额是该公司对三个村的投资总额的和的 ,则该公司对B村的投资总额与该公司对C村的投资总额的比为.
18. 某公司对A村、B村、C村进行了合作办企的投资,其投资总额是对C村投资额的 倍.随着国家对乡村振兴的高度重视,该公司调整了投资计划,在原投资总额的基础上再增加一部分投资,并按3:3:8的比例分别对A村、B村、C村增加投资.该公司调整投资计划后,若该公司对A村的投资总额与该公司对三个村的投资总额的和的比为6:13,且该公司对B村增加的投资额是该公司对三个村的投资总额的和的 ,则该公司对B村的投资总额与该公司对C村的投资总额的比为.三、解答题
-
19. 计算:(1)、(2)、20. 如图,在平行四边形 中, 平分 交 于点F.
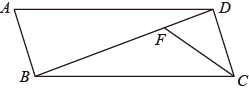 (1)、尺规作图:过点A作 平分 交 于点E;注意:不写作法,保留作图痕迹,并标明字母.(2)、求证: .21. 在开展“童心向党”系列活动中,某校举办了一场“党史知识你我知”的知识竞赛,现分别从八年级、九年级各随机抽取了20名学生的成绩(单位:分,满分:100分),相关数据(成绩)整理统计如下:
(1)、尺规作图:过点A作 平分 交 于点E;注意:不写作法,保留作图痕迹,并标明字母.(2)、求证: .21. 在开展“童心向党”系列活动中,某校举办了一场“党史知识你我知”的知识竞赛,现分别从八年级、九年级各随机抽取了20名学生的成绩(单位:分,满分:100分),相关数据(成绩)整理统计如下:收集数据:
八年级:92,98,96,93,96,92,60,92,78,92,86,84,81,84,78,92,74,100,64,92.
九年级:93,88,89,96,72,75,95,90,86,95,95,96,100,94,93,68,86,80,78,91.
整理数据:
八年级
2
3
4
11
九年级
1
3
5
11
分析数据:
平均数
中位数
众数
八年级
86.2
a
92
九年级
88
92
b
根据以上信息回答下列问题:
(1)、请直接写出表中的a,b的值;(2)、已知该校八、九年级各有学生760人,若规定知识竞赛成绩在80分及其以上为优秀,请估计该校知识竞赛成绩为优秀的学生人数;(3)、根据表中的统计量,你认为哪个年级的知识竞赛成绩的总体水平更好,请说明理由.22. 在学习数学的过程中,我们发现了一种很有趣的自然数——“登高数”.定义:设一个四位正整数的千位、百位、十位、个位上的数字分别为a,b,c,d,且 ,若 的值能被 的值整除,则称这个正整数为“登高数”.例如:1345是“登高数”,因为1,3,4,5都不为0, ,且 ,且12能被6整除,所以1345是“登高数”;2457不是“登高数”,因为2,4,5,7都不为0, ,且 , ,但20不能被9整除,所以2457不是“登高数”
(1)、判断3567,2589是否是“登高数”,并说明理由;(2)、在四位正整数中,求出百位上的数字比个位上的数字小5的所有“登高数”.23. 在学习函数的过程中,我们经历了通过列表,描点,连线来画函数图象,观察分析图象特征,从而概括出函数的性质的过程.下面是研究函数 ,性质及其应用的部分过程.请按要求完成下列各小题.
列表:
x
…
-3
-2
-1
0
2
3
…
y
…
4
a
0
1
2
1
b
…
(1)、请求出表中a,b的值,并在图中补全该函数的图象;(2)、根据函数图象,写出该函数的一条性质;(3)、已知函数 的图象如图所示,结合你所画的函数图象,请直接写出不等式 的解集.24. 一时蔬小店某一天用150元购进了30斤平菇和20斤莴笋.销售时,每斤平菇的平均售价比每斤莴笋的平均售价的2倍少1元,该小店销售完所进的平菇和莴笋后获利60元.(1)、这一天,该小店销售莴笋的平均售价是每斤多少元?(2)、接着第二天,该小店又用150元购进了30斤平菇和20斤莴笋,其中,平菇和莴笋的进价与第一天的进价相同.销售时受到一些因素的影响,每斤莴笋的平均售价比第一天的平均售价增加了 ,但莴笋的销售量与第一天的销售量相同;每斤平菇的平均售价比第一天的平均售价增加了 ,但平菇的销售量比第一天的销售量下降了 ,最终第二天的总销售额与第一天的总销售额相等,求a的值.25. 如图,已知抛物线 经过三点 . (1)、求a,b,c的值;(2)、若点P是直线 下方抛物线上的一点,连接 ,求 面积的最大值;(3)、将原抛物线 向右平移4个单位长度,得到新抛物线 ,点Q是x轴上方新抛物线上一点,当 的面积取最大值时,在x轴上是否存在点N,使得以点A、N、P、Q为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标,若不存在,请说明理由.26. 如图①,在矩形 中, ,矩形 是由矩形 绕点C顺时针旋转一个角度得到的,点 分别是点A、B、D的对应点.在旋转过程中,直线 与直线 相交于点M.
(1)、求a,b,c的值;(2)、若点P是直线 下方抛物线上的一点,连接 ,求 面积的最大值;(3)、将原抛物线 向右平移4个单位长度,得到新抛物线 ,点Q是x轴上方新抛物线上一点,当 的面积取最大值时,在x轴上是否存在点N,使得以点A、N、P、Q为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标,若不存在,请说明理由.26. 如图①,在矩形 中, ,矩形 是由矩形 绕点C顺时针旋转一个角度得到的,点 分别是点A、B、D的对应点.在旋转过程中,直线 与直线 相交于点M.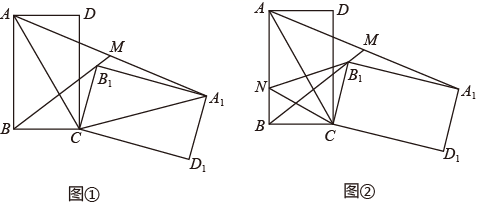 (1)、当 时,求 的度数;(2)、在旋转过程中,请你猜想 与 之间存在的数量关系,并根据所给图形证明你猜想的结论;(3)、如图②,设点N在边 上,且∠ ,在旋转过程中,当 的值取最小值时,请直接写出点 与点M之间的距离.
(1)、当 时,求 的度数;(2)、在旋转过程中,请你猜想 与 之间存在的数量关系,并根据所给图形证明你猜想的结论;(3)、如图②,设点N在边 上,且∠ ,在旋转过程中,当 的值取最小值时,请直接写出点 与点M之间的距离.