江苏省扬州市广陵区2021年数学中考一模试卷
试卷更新日期:2021-11-03 类型:中考模拟
一、单选题
-
1. -2的倒数是( )A、 B、 C、±2 D、22. 函数 中自变量 的取值范围是( )A、 B、 C、 D、3. 下列各式中,计算结果为 的是( )A、 B、 C、 D、4. 某几何体的三视图如图所示,则该几何体是( )
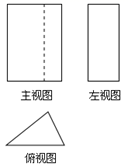 A、三棱锥 B、三棱柱 C、四棱柱 D、四棱锥5. 已知某圆锥的底面半径为3cm,母线长5cm,则它的侧面展开图的面积为( )A、30cm2 B、15cm2 C、30πcm2 D、15πcm26. 小敏参加了某次演讲比赛,根据比赛时七位评委所给的分数制作了如下表格:
A、三棱锥 B、三棱柱 C、四棱柱 D、四棱锥5. 已知某圆锥的底面半径为3cm,母线长5cm,则它的侧面展开图的面积为( )A、30cm2 B、15cm2 C、30πcm2 D、15πcm26. 小敏参加了某次演讲比赛,根据比赛时七位评委所给的分数制作了如下表格:平均数/分
中位数/分
众数/分
方差/分2
8.8
8.9
8.5
0.14
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( )
A、平均数 B、中位数 C、众数 D、方差7. 如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α , ∠ADC=β , 则竹竿AB与AD的长度之比为( )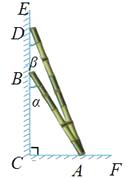 A、 B、 C、 D、8. 如图,在平面直角坐标系 中,正方形 的顶点坐标分别为 、 、 、 ,点 绕点A旋转 得点 ,点 绕点B旋转 得点 ,点 绕点C旋转 得点 ,点 绕点D旋转 得点 ,点 绕点A旋转 得点 ,……,重复操作依次得到点 , , , , ,……,则点 的坐标为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系 中,正方形 的顶点坐标分别为 、 、 、 ,点 绕点A旋转 得点 ,点 绕点B旋转 得点 ,点 绕点C旋转 得点 ,点 绕点D旋转 得点 ,点 绕点A旋转 得点 ,……,重复操作依次得到点 , , , , ,……,则点 的坐标为( )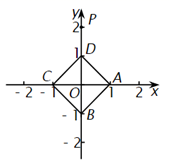 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 截止2021年3月31日,扬州高铁东站已经输送旅客约1200000人次.用科学记数法表示1200000是.10. 分解因式: =.11. 方程(x+1)(x-3)=-4的解为.12. 已知反比例函数 ,y随x的增大而增大,则m的取值范围是.13. 下表记录了一名篮球运动员在罚球线上投篮的结果:
投篮次数n
48
82
124
176
230
287
328
投中次数m
33
59
83
118
159
195
223
投中频率
0.69
0.72
0.67
0.67
0.69
0.68
0.68
根据上表,这名篮球运动员投篮一次,投中的概率约为.
14. 命题“对顶角相等”的逆命题是一个命题(填“真”或“假”).15. 如图,四边形 是 的内接四边形,若 半径为4,且 ,则 的长为.(结果保留π)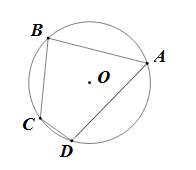 16. 如图,在 中, , , , 平分 交 于点D,则 .
16. 如图,在 中, , , , 平分 交 于点D,则 .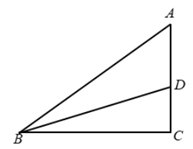 17. 若一次函数y=kx+b,当-3≤x≤1时,对应的y值满足1≤y≤9,则一次函数的解析式为.18. 如图,矩形 中, , , 为边 上一个动点,连结 ,取 的中 点 ,点 绕点 逆时针旋转 得到点 ,连结 ,则 面积的最小值是.
17. 若一次函数y=kx+b,当-3≤x≤1时,对应的y值满足1≤y≤9,则一次函数的解析式为.18. 如图,矩形 中, , , 为边 上一个动点,连结 ,取 的中 点 ,点 绕点 逆时针旋转 得到点 ,连结 ,则 面积的最小值是.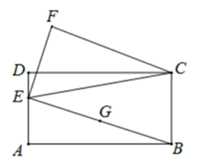
三、解答题
-
19. 计算或化简:(1)、计算:(2)、化简:20. 解不等式组 ,并求其整数解.21. 中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
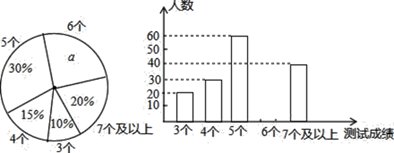 (1)、写出扇形图中 ▲ %,并补全条形图;(2)、在这次抽测中,测试成绩的众数和中位数分别是个,个;(3)、该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?22. 甲、乙、丙3名医生志愿报名参加新冠肺炎救治工作.(1)、随机抽取1名,则恰是甲的概率是;(2)、随机抽取2名,求甲在其中的概率.23. 为支援非洲人民战胜疫情,某疫苗生产厂家在清明节期间接到紧急任务,要求在几天内生产700万支疫苗.疫苗厂干部职工放弃休息时间,开足全厂疫苗生产线进行生产,结果每天比原来多生产30万支,提前3天完成了任务.原来要求几天完成这项紧急任务?24. 如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
(1)、写出扇形图中 ▲ %,并补全条形图;(2)、在这次抽测中,测试成绩的众数和中位数分别是个,个;(3)、该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?22. 甲、乙、丙3名医生志愿报名参加新冠肺炎救治工作.(1)、随机抽取1名,则恰是甲的概率是;(2)、随机抽取2名,求甲在其中的概率.23. 为支援非洲人民战胜疫情,某疫苗生产厂家在清明节期间接到紧急任务,要求在几天内生产700万支疫苗.疫苗厂干部职工放弃休息时间,开足全厂疫苗生产线进行生产,结果每天比原来多生产30万支,提前3天完成了任务.原来要求几天完成这项紧急任务?24. 如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.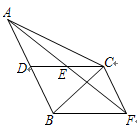 (1)、求证:CF=AD;(2)、若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.25. 如图,点 在 的 边上, 经过点 、 ,且与 相交于点 .点 是下半圆弧的中点,连接 交 于点 ,已知 .
(1)、求证:CF=AD;(2)、若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.25. 如图,点 在 的 边上, 经过点 、 ,且与 相交于点 .点 是下半圆弧的中点,连接 交 于点 ,已知 .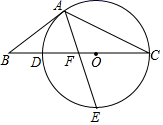 (1)、求证: 是 的切线;(2)、若 , ,求 的值.26. 请阅读下列材料
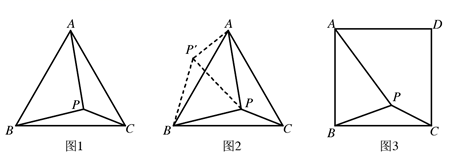
(1)、求证: 是 的切线;(2)、若 , ,求 的值.26. 请阅读下列材料问题:如图1,在等边三角形 内有一点 ,且 , , .求 度数的大小和等边三角形 的边长.
李明同学的思路是:将 绕点 顺时针旋转 ,画出旋转后的图形(如图2).连接 ,可得 是等边三角形, 又是直角三角形(由勾股定理的逆定理可证).所以 ,而 .进而求出等边 的边长为 ,问题得到解决.
请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形 内有一点 ,且 , , .求 度数的大小和正方形 的边长.
 27. 如图,在边长为6的等边 中,D是 边上一点, ,E是 边上一动点, 交 边于F.
27. 如图,在边长为6的等边 中,D是 边上一点, ,E是 边上一动点, 交 边于F.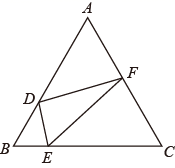 (1)、找出图中一对相似三角形,并说明理由;(2)、在点E从B点运动到C点的过程中:
(1)、找出图中一对相似三角形,并说明理由;(2)、在点E从B点运动到C点的过程中:①求 长的最小值;
②线段 的中点所经过的路径长为 ;线段 的中点到 的最大距离为 .
28. 已知,点 为二次函数 图象的顶点,直线 分别交 轴正半轴, 轴于点 , .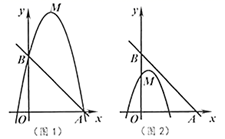 (1)、判断顶点 是否在直线 上,并说明理由.(2)、如图1,若二次函数图象也经过点 , ,且 ,根据图象,写出 的取值范围.(3)、如图2,点 坐标为 ,点 在 内,若点 , 都在二次函数图象上,试比较 与 的大小.
(1)、判断顶点 是否在直线 上,并说明理由.(2)、如图1,若二次函数图象也经过点 , ,且 ,根据图象,写出 的取值范围.(3)、如图2,点 坐标为 ,点 在 内,若点 , 都在二次函数图象上,试比较 与 的大小.