江苏省苏州市高新区阳山实验2021年数学中考二模试卷

试卷更新日期：2021-11-03 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，如果数轴上 $A$ ， $B$ 两点之间的距离是3，且点 $B$ 在原点左侧，那么点 $B$ 表示的数是（）

A、3 B、-3 C、1 D、-1

查看试题解析
2. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、等边三角形 B、平行四边形 C、矩形 D、正五边形

查看试题解析
3. 下列运算正确的是（）

A、2a ＋3b ＝ 5ab B、a²·a³＝a⁵ C、(2a)³ ＝ 6a³ D、a⁶＋a³＝ a⁹

查看试题解析
4. 如图，平行线 $A B$ 、 $C D$ 被直线 $E F$ 所截，过点 $B$ 作 $B G ⊥ E F$ 于点 $G$ ，已知 $∠ 1 = 50 °$ ，则 $∠ B =$ （）.

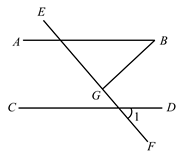A、20° B、30° C、40° D、50°

查看试题解析
5. 如图所示，该几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
6. 如图，已知 $⊙ O$ 是 $△ A B C$ 的外接圆，连接 $O A$ ，若 $∠ B = 70 °$ ，则 $∠ O A C$ 的度数为（）

A、 $20 °$ B、 $25 °$ C、 $50 °$ D、 $65 °$

查看试题解析
7. 王老师对小明在参加中考前的5次数学模拟考试成绩进行统计分析，要判断小明的数学成绩是否稳定，老师需要知道小明这5次数学成绩的（）

A、频数 B、众数 C、中位数 D、方差

查看试题解析
8. 古希腊艺术家发现当人的头顶至肚脐的长度（上半身的长度）与肚脐至足底的长度（下半身的长度）的比值为“黄金分割数”时，人体的身材是最优美的，一位女士身高为154cm，她上半身的长度为62cm，为了使自己的身材显得更为优美，计划选择一双合适的高跟鞋，使自己的下半身长度增加，你认为选择鞋跟高为多少厘米的高跟鞋最佳（）

A、4cm B、6cm C、8cm D、10cm

查看试题解析
9. 已知一次函数 $y_{1} = k_{1} x + b_{1}$ （ $k_{1}$ ， $b_{1}$ 为常数， $k_{1} \neq 0$ ）， $y_{2} = k_{2} x + b_{2}$ （ $k_{2}$ ， $b_{2}$ 为常数， $k_{2} \neq 0$ ）的图象如图所示，则函数 $y = y_{1} \cdot y_{2}$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图，在等边 $△ A B C$ 中， $B C = 6$ ，点E在中线 $A D$ 上，现有一动点P沿着折线 $A - E - C$ 运动，且在 $A E$ 上的速度是4单位/秒，在 $E C$ 上的速度是2单位/秒，当点P从A运动到C所用时间最少时， $A E$ 长为（）

A、3 B、 $\sqrt{3}$ C、 $\frac{3 \sqrt{3}}{2}$ D、 $2 \sqrt{3}$

查看试题解析

二、填空题

11. 8的立方根是．

查看试题解析
12. 总值约为1020000亿元，将数字1020000亿用科学记数法表示为.

查看试题解析
13. 分解因式： ${ab}^{2}$ -25a =

查看试题解析
14. 已知一个扇形的圆心角为 $45 °$ ，半径为3，将这个扇形围成一个圆锥，则这个圆锥的底面圆半径为.

查看试题解析
15. 2022年在北京将举办第24届冬季奥运会，很多学校都开展了冰雪项目学习.如图，滑雪轨道由AB、BC两部分组成，AB、BC的长度都为200米，一位同学乘滑雪板沿此轨道由A点滑到了C点，若AB与水平面的夹角 $α$ 为30°，BC与水平面的夹角 $β$ 为45°，则他下降的高度为米（结果保留根号）.

查看试题解析
16. 已知关于x的分式方程 $\frac{x}{x - 2} - 4 = \frac{k}{2 - x}$ 的解为正数，则k的取值范围是

查看试题解析
17. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90^{°}$ ， $A B = 5$ ， $B C = 3$ ，点P在边AC上， $⊙ P$ 的半径为1，如果 $⊙ P$ 与边BC和边AB都没有公共点，那么线段PC长的取值范围是.

查看试题解析
18. 如果四边形边上的点，它与对边两个端点的连线将这个四边形分成的三个三角形都相似，我们就把这个点叫做该四边形的“强相似点”.如图1，在四边形 $A B C D$ 中，点 $Q$ 在边 $A D$ 上，如果 $△ Q A B$ 、 $△ Q B C$ 和 $△ Q D C$ 都相似，那么点 $Q$ 就是四边形 $A B C D$ 的“强相似点”；如图2，在四边形 $A B C D$ 中， $A D ⁄ ⁄ B C$ ， $A B = D C = 2$ ， $B C = 8$ ， $∠ B = 60 °$ ，如果点 $Q$ 是边 $A D$ 上的“强相似点”，那么 $A Q =$ .

查看试题解析

三、解答题

19.

(1)、计算： $- 2^{2} + {(\sqrt{3} - π)}^{0} + | 1 - \sin 60 ° |$

(2)、解方程组： ${\begin{array}{l} 2 x + y = 1 \\ x - 2 y = 3 \end{array}$ .

查看试题解析
20. 先化简，再求值： $(1 - \frac{5}{x + 2}) \div \frac{x^{2} - 9}{x + 3}$ ，其中 $x = \sqrt{3} - 2$ ．

查看试题解析

21. 某公司共有A，B，C三个部门，根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.

各部门人数及每人所创年利润统计表

部门	员工人数	每人所创的年利润/万元
A	5	10
B		8
C		5

(1)、①在扇形图中，C部门所对应的圆心角的度数为；

②在统计表中，b= ， c=；

(2)、求这个公司平均每人所创年利润.

查看试题解析

22. 一个 $3 \times 3$ 的棋盘，在棋盘方格内随机放入棋子，且每一方格内最多放入一枚棋子.

(1)、如图①，棋盘内已有两枚棋子，在剩余的方格内随机放入一枚棋子，这三枚棋子恰好能在同一条直线上的概率为；

(2)、如图②，棋盘内已有四枚棋子，在剩余的方格内随机放入两枚棋子，求仅有三枚棋子恰好能在同一条直线上的概率.

查看试题解析
23. 在平面直角坐标系 $x O y$ 中，反比例函数 $y = \frac{6}{x}$ 的图象与一次函数 $y = k x - 1$ 的图象相交于横坐标为 $3$ 的点 $A$ .

(1)、求这个一次函数的解析式；

(2)、如图，已知点 $B$ 在这个一次函数图象上，点 $C$ 在反比例函数 $y = \frac{6}{x}$ 的图象上，直线 $B C //x$ 轴，且在点 $A$ 上方，并与 $y$ 轴相交于点 $D$ .如果点 $C$ 恰好是 $B D$ 的中点，求点 $B$ 的坐标.

查看试题解析
24. 如图，在矩形ABCD中，AB＝2BC，F、G分别为AB、DC边上的动点，连接GF，沿GF将四边形AFGD翻折至四边形EFGP，点E落在BC上，EP交CD于点H，连接AE交GF于点O.

(1)、写出GF与AE之间的位置关系是：，

(2)、求证：AE＝2GF

(3)、连接CP，若sin∠CGP＝ $\frac{3}{5}$ ，GF＝ $\sqrt{10}$ ，求CE的长.

查看试题解析
25. 如图，是小明家房屋的纵截面图，其中线段 $A B$ 为屋内地面，线段 $A E$ 、 $B C$ 为房屋两侧的墙，线段 $C D$ 、 $D E$ 为屋顶的斜坡.已知 $A B = 6$ 米， $A E = B C = 3.2$ 米，斜坡 $C D$ 、 $D E$ 的坡比均为1∶2.（参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ， $\sqrt{5} \approx 2.24$ ， $\sqrt{10} \approx 3.16$ ， $\sin 53 ° = 0.8$ ， $\cos 53 ° = 0.6$ ， $\tan 53 ° = \frac{4}{3}$ .）

(1)、求屋顶点D到地面 $A B$ 的距离：

(2)、已知在墙 $A E$ 距离地面1.1米处装有窗 $S T$ ，如果阳光与地面的夹角 $∠ M N P = β = 53 °$ ，为了防止阳光通过窗 $S T$ 照射到屋内，所以小明请门窗公司在墙 $A E$ 端点E处安装一个旋转式遮阳棚（如图中线段 $E F$ ），公司设计的遮阳棚可作90°旋转，即 $0 ° < ∠ F E T = α \leq 90 °$ ，长度为1.4米，即 $E F = 1.4$ 米.试问：公司设计的遮阳棚是否能达到小明的要求？说说你的理由.

查看试题解析
26. 如图，在 $△ A B C$ 中， $D$ 是 $B C$ 边上的点，过点 $D$ 作 $D E ⊥ B C$ 交 $A C$ 边于点 $E$ ，垂足为 $D$ ，过点 $D$ 作 $D F ⊥ A B$ ，垂足为 $F$ ，连接 $E F$ ，经过点 $D$ ， $E$ ， $F$ 的 $O$ 与边 $B C$ 另一个公共点为 $G$ .

(1)、连接 $G F$ ，求证 $△ B G F \sim △ D E F$ ；

(2)、若 $A B = A C$ ， $B C = 4$ ， $\tan C = 2$ .
①当 $C D = 1.5$ 时，求 $O$ 的半径；

②当点 $D$ 在 $B C$ 边上运动时， $O$ 半径的最小值为 ▲ .

查看试题解析
27. 已知： $∠ A O C = ∠ B O C = 60 °$ ，过平面内一点 $P$ 分别向 $O A$ 、 $O B$ 、 $O C$ 画垂线，垂足分别为 $D$ 、 $E$ 、 $F$ .

(1)、（问题引入）
如图①，当点 $P$ 在射线 $O C$ 上时，求证： $O D = O E$ .

(2)、（类比探究）
如图②，当点 $P$ 在 $∠ A O C$ 内部，点 $E$ 在射线 $O B$ 上时，求证： $O D + O E = O F$ .

(3)、当点 $P$ 在 $∠ A O C$ 内部，点 $E$ 在射线 $O B$ 的反向延长线上时，在图③中画出示意图，并直接写出线段 $O D$ 、 $O E$ 、 $O F$ 之间的数量关系.

(4)、（知识拓展）
如图④， $A B$ 、 $C D$ 、 $E F$ 是 $⊙ O$ 的三条弦，都经过圆内一点 $P$ ，且 $∠ F P D = ∠ B P D = 60 °$ .判断 $P A + P D + P E$ 与 $P B + P C + P F$ 的数量关系，并证明你的结论.

查看试题解析
28. 如图，已知抛物线 $y = a x^{2} + 4 a x - 3$ 与x轴交于A、B两点（A在B的左侧），与y轴交于点C，过点B的直线l与抛物线另一个交点为D，与y轴交于点E，且 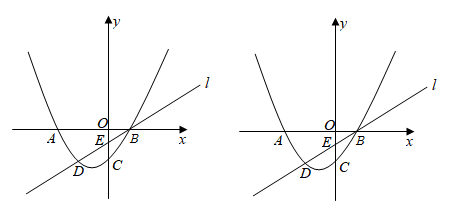$D E = 2 E B$ ，点A的坐标 $(- 6 ， 0)$ .

(1)、求抛物线的函数表达式；

(2)、若P是抛物线上的一点，P的横坐标为 $m (m < 0)$ ，过点P作 $P H ⊥ x$ 轴，垂足为H，直线 $P H$ 与l交于点M.
①若 $C M$ 将 $△ C H P$ 的面积分为1：2两部分，求点P的坐标；

②当 $m = - 2$ 时，直线 $P H$ 上是否存在一点Q，使 $∠ Q D B = 45 °$ ？如果存在，求出点Q的坐标；如果不存在，请说明理由

查看试题解析