江苏省苏州市高新区新区一中2021年数学中考二模试卷
试卷更新日期:2021-11-03 类型:中考模拟
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 实数a在数轴上的对应点的位置如图所示.若实数 满足 ,则b的值可以是( )
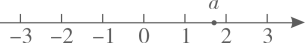 A、2 B、-1 C、-2 D、-33. 若一个多边形的每个外角都为36°,则这个多边形是( )A、六边形 B、八边形 C、十边形 D、十二边形4. 若代数式 有意义,则实数x的取值范围是( )A、 B、 C、 D、5. 如图所示,该几何体的俯视图是( )
A、2 B、-1 C、-2 D、-33. 若一个多边形的每个外角都为36°,则这个多边形是( )A、六边形 B、八边形 C、十边形 D、十二边形4. 若代数式 有意义,则实数x的取值范围是( )A、 B、 C、 D、5. 如图所示,该几何体的俯视图是( )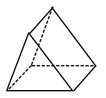 A、
A、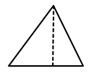 B、
B、 C、
C、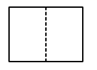 D、
D、 6. 下列说法正确的是( )A、为了解人造卫星的设备零件的质量情况,选择抽样调查 B、方差是刻画数据波动程度的量 C、购买一张体育彩票必中奖,是不可能事件 D、掷一枚质地均匀的硬币,正面朝上的概率为17. 如图 是 切线,点A为切点, 交 于点C,点D在 上,连接 ,若 ,则 的度数为( )
6. 下列说法正确的是( )A、为了解人造卫星的设备零件的质量情况,选择抽样调查 B、方差是刻画数据波动程度的量 C、购买一张体育彩票必中奖,是不可能事件 D、掷一枚质地均匀的硬币,正面朝上的概率为17. 如图 是 切线,点A为切点, 交 于点C,点D在 上,连接 ,若 ,则 的度数为( )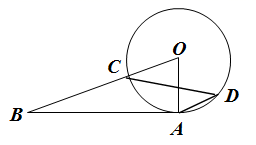 A、25° B、20° C、30° D、35°8. 如图,直线 和 相交于点 ,则不等式 的解集为( )
A、25° B、20° C、30° D、35°8. 如图,直线 和 相交于点 ,则不等式 的解集为( )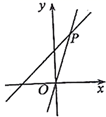 A、 B、 C、 D、9. 如图,在△ABC中,AD,BE分别是BC,AC边上的中线,且AD⊥BE,垂足为点F,设BC=a,AC=b,AB=c,则下列关系式中成立的是( )
A、 B、 C、 D、9. 如图,在△ABC中,AD,BE分别是BC,AC边上的中线,且AD⊥BE,垂足为点F,设BC=a,AC=b,AB=c,则下列关系式中成立的是( ) A、a2+b2=5c2 B、a2+b2=4c2 C、a2+b2=3c2 D、a2+b2=2c210. 已知二次函数 (其中x是自变量)的图象经过不同两点 , ,且该二次函数的图象与x轴有公共点,则 的值( )A、-1 B、2 C、3 D、4
A、a2+b2=5c2 B、a2+b2=4c2 C、a2+b2=3c2 D、a2+b2=2c210. 已知二次函数 (其中x是自变量)的图象经过不同两点 , ,且该二次函数的图象与x轴有公共点,则 的值( )A、-1 B、2 C、3 D、4二、填空题
-
11. 新冠肺炎疫情期间,全国各地约42000名医护人员驰援湖北.请将数42000用科学记数法表示为 .12. 已知关于 的方程 有两个相等的实数根,则k的值是 .13. 分解因式: =14. 如图所示的网格是正方形网格,A,B,C,D是网格交点,则 ABC的面积与 ABD的面积的大小关系为: (填“>”,“=”或“<”)
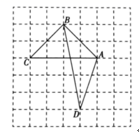 15. 已知 ,则 .16. 一个扇形的面积为 ,半径为6cm,则扇形的圆心角是度.17. 在△ABC和△A1B1C1中,已知∠C=∠C1=90°,AC=A1C1=3,BC=4,B1C1=2,点D、D1分别在边AB、A1B1上,且 ,那么AD的长是.18. 如图,A、B两点在反比例函数 的图象上,C、D两点在反比例函数 的图象上, 轴于点E, 轴于点F, ,则 .
15. 已知 ,则 .16. 一个扇形的面积为 ,半径为6cm,则扇形的圆心角是度.17. 在△ABC和△A1B1C1中,已知∠C=∠C1=90°,AC=A1C1=3,BC=4,B1C1=2,点D、D1分别在边AB、A1B1上,且 ,那么AD的长是.18. 如图,A、B两点在反比例函数 的图象上,C、D两点在反比例函数 的图象上, 轴于点E, 轴于点F, ,则 .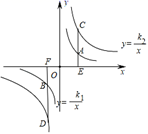
三、解答题
-
19. 计算:20. 先化简,再求值: ,其中a=2.21. 解不等式组: 并在数轴上把解集表示出来.
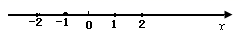 22. 如图,点A,C,B,D在同一条直线上,BE∥DF,∠A=∠F,AB=FD,求证:AE=FC.
22. 如图,点A,C,B,D在同一条直线上,BE∥DF,∠A=∠F,AB=FD,求证:AE=FC.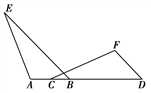 23. 我市某中学举行“法制进校园”知识竞赛,赛后将学生的成绩分为A、B、C、D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图.请你根据统计图解答下列问题.
23. 我市某中学举行“法制进校园”知识竞赛,赛后将学生的成绩分为A、B、C、D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图.请你根据统计图解答下列问题.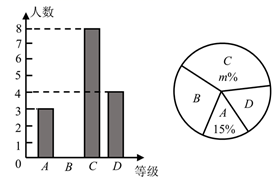 (1)、成绩为“B等级”的学生人数有名;(2)、在扇形统计图中,表示“D等级”的扇形的圆心角度数为 , 图中m的值为;(3)、学校决定从本次比赛获得“A等级”的学生中选出2名去参加市中学生知识竞赛.已知“A等级”中有1名女生,请用列表或画树状图的方法求出女生被选中的概率.24. 如图1是一种台灯,其主体部分是由与桌面垂直的固定灯杆 和可转动灯杆 和光源 组成,当灯杆 绕点B转动时,光线在桌面上的圆形照明区域随着光源到桌面的距离发生改变.图2是其示意图,其中 , ,灯杆 , .
(1)、成绩为“B等级”的学生人数有名;(2)、在扇形统计图中,表示“D等级”的扇形的圆心角度数为 , 图中m的值为;(3)、学校决定从本次比赛获得“A等级”的学生中选出2名去参加市中学生知识竞赛.已知“A等级”中有1名女生,请用列表或画树状图的方法求出女生被选中的概率.24. 如图1是一种台灯,其主体部分是由与桌面垂直的固定灯杆 和可转动灯杆 和光源 组成,当灯杆 绕点B转动时,光线在桌面上的圆形照明区域随着光源到桌面的距离发生改变.图2是其示意图,其中 , ,灯杆 , .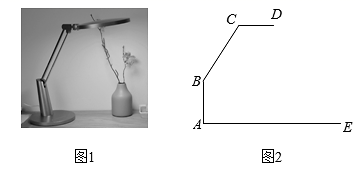 (1)、当灯杆 与 的夹角 为150°时,求光源 到桌面 的距离;(2)、若光源 到 的距离h与圆形照明区域半径r的关系是 ,要使圆形区域半径达到 ,求灯杆 与 的夹角 的度数.25. “节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:(1)、A型自行车去年每辆售价多少元;(2)、该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多.26. 在平面直角坐标系 中,如果抛物线 上存在一点A,使点A关于坐标原点O的对称点 也在这条抛物线上,那么我们把这条抛物线叫做回归地物线,点A叫做这条抛物线的回归点.(1)、已知点M在抛物线 上,且点M的横坐标为2,试判断抛物线 是否为回归抛物线,并说明理由;(2)、已知点C为回归抛物线 的顶点,如果点C是这条抛物线的回归点,求这条抛物线的表达式;27. 在平面直角坐标系xOy中,⊙C的半径为r(r>1),P是圆内与圆心C不重合的点,⊙C的“完美点”的定义如下:若直线CP与⊙C交于点A,B,满足|PA﹣PB|=2,则称点P为⊙C的“完美点”,如图为⊙C及其“完美点”P的示意图.
(1)、当灯杆 与 的夹角 为150°时,求光源 到桌面 的距离;(2)、若光源 到 的距离h与圆形照明区域半径r的关系是 ,要使圆形区域半径达到 ,求灯杆 与 的夹角 的度数.25. “节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:(1)、A型自行车去年每辆售价多少元;(2)、该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多.26. 在平面直角坐标系 中,如果抛物线 上存在一点A,使点A关于坐标原点O的对称点 也在这条抛物线上,那么我们把这条抛物线叫做回归地物线,点A叫做这条抛物线的回归点.(1)、已知点M在抛物线 上,且点M的横坐标为2,试判断抛物线 是否为回归抛物线,并说明理由;(2)、已知点C为回归抛物线 的顶点,如果点C是这条抛物线的回归点,求这条抛物线的表达式;27. 在平面直角坐标系xOy中,⊙C的半径为r(r>1),P是圆内与圆心C不重合的点,⊙C的“完美点”的定义如下:若直线CP与⊙C交于点A,B,满足|PA﹣PB|=2,则称点P为⊙C的“完美点”,如图为⊙C及其“完美点”P的示意图.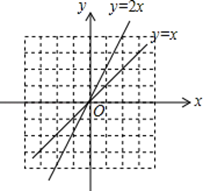
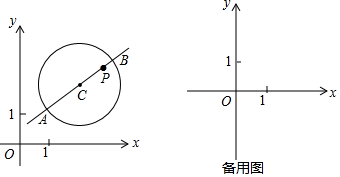 (1)、当⊙O的半径为2时,
(1)、当⊙O的半径为2时,①在点M ,N(0,1),T 中,⊙O的“完美点”是▲;
②若⊙O的“完美点”P在直线y= x上,求PO的长及点P的坐标;
(2)、⊙C的圆心在直线y= x+1上,半径为2,若y轴上存在⊙C的“完美点”,求圆心C的纵坐标t的取值范围.28. 定义:如果一个三角形一条边上的高与这条边的比值是3:5,那么称这个三角形为“准黄金”三角形,这条边就叫做这个三角形的“金底”.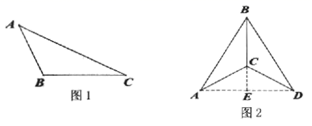
 (1)、(概念感知)
(1)、(概念感知)
如图1,在 中, , , ,试判断 是否是“准黄金”三角形,请说明理由.(2)、(问题探究)
如图2, 是“准黄金”三角形,BC是“金底”,把 沿BC翻折得到 ,连AB接AD交BC的延长线于点E,若点C恰好是 的重心,求 的值.(3)、(拓展提升)
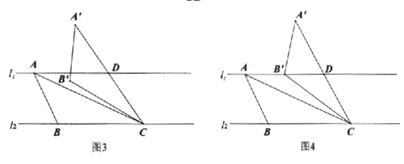
如图3, ,且直线 与 之间的距离为3,“准黄金” 的“金底”BC在直线 上,点A在直线 上. ,若 是钝角,将 绕点 按顺时针方向旋转 得到 ,线段 交 于点D.①当 时,则 ▲ ;
②如图4,当点B落在直线 上时,求 的值.