湖南省长沙市长郡教育集团2021年数学中考二模试卷
试卷更新日期:2021-11-03 类型:中考模拟
一、单选题
-
1. 下列各数中是有理数的是( )A、2021 B、 C、 D、0.1010010001…2. 根据国家卫健委最新数据,截至到2021年4月2日,全国各地累计报告接种新冠病毒疫苗133801000剂次,将133801000用科学记数法表示为( ).A、 B、 C、 D、3. 下列图形一定是轴对称图形的是( )A、直角三角形 B、平行四边形 C、等腰三角形 D、六边形4. 下列计算中,结果是 的是( )A、 B、 C、 D、5. 如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
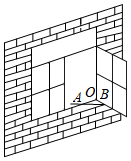 A、两点确定一条直线 B、两点之间线段最短 C、三角形的稳定性 D、垂线段最短6. 有7名大学生去同一家公司面试,公司只录取3人,每个人仅知道自己的面试成绩(每个人的面试成绩都不相同),要想让他们知道是否被录取,公司只需公布他们面试成绩的( )A、平均数 B、中位数 C、众数 D、方差7. 要使 有意义,则x的取值范围为( )A、x≤0 B、x≥1 C、x≥0 D、x≤18. 如图,将线段 平移到线段 的位置,则a-b的值为( )
A、两点确定一条直线 B、两点之间线段最短 C、三角形的稳定性 D、垂线段最短6. 有7名大学生去同一家公司面试,公司只录取3人,每个人仅知道自己的面试成绩(每个人的面试成绩都不相同),要想让他们知道是否被录取,公司只需公布他们面试成绩的( )A、平均数 B、中位数 C、众数 D、方差7. 要使 有意义,则x的取值范围为( )A、x≤0 B、x≥1 C、x≥0 D、x≤18. 如图,将线段 平移到线段 的位置,则a-b的值为( ) A、4 B、0 C、3 D、9. 下列说法正确的是( )A、4的平方根是2 B、平分弦的直径垂直弦并平分弦所对的弧 C、一组数据中有且仅有一个众数 D、等弧所对的弦相等10. 如图,这是一个底面为等边三角形的正三棱柱和它的主视图、俯视图,则它的左视图的面积是( )
A、4 B、0 C、3 D、9. 下列说法正确的是( )A、4的平方根是2 B、平分弦的直径垂直弦并平分弦所对的弧 C、一组数据中有且仅有一个众数 D、等弧所对的弦相等10. 如图,这是一个底面为等边三角形的正三棱柱和它的主视图、俯视图,则它的左视图的面积是( )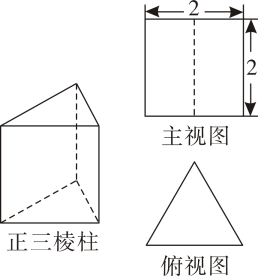 A、4 B、2 C、 D、
A、4 B、2 C、 D、二、填空题
-
11. 一元一次方程 的解是 .12. 笔直的公路 , , 如图所示, , 互相垂直, 的中点D与点C被建筑物隔开,若测得 的长为 , 的长为 ,则C,D之间的距离为 .
 13. 在平面直角坐标系中已知点 , ,以原点 为位似中心,相似比为1:2,将 扩大,则点 的对应点 的坐标是 .14. 如图所示,AB DE,∠1=130°,∠2=36°,则∠3等于.
13. 在平面直角坐标系中已知点 , ,以原点 为位似中心,相似比为1:2,将 扩大,则点 的对应点 的坐标是 .14. 如图所示,AB DE,∠1=130°,∠2=36°,则∠3等于. 15. 如图,一次函数y=k1x+b的图象与反比例函数y= 的图象相交于A(2,3),B(6,1)两点,当k1x+b< 时,x的取值范围为.
15. 如图,一次函数y=k1x+b的图象与反比例函数y= 的图象相交于A(2,3),B(6,1)两点,当k1x+b< 时,x的取值范围为. 16. 如图,矩形 中,点E在 上,过点E作 交 于F,且 , ,点M是线段 上的动点,连接 ,过点E作 的垂线交 于点N,垂足为H.以下结论:① ;② ;③ ;④连接 ,则 的最小值为 ;其中正确的结论是.(所有正确结论的序号都填上).
16. 如图,矩形 中,点E在 上,过点E作 交 于F,且 , ,点M是线段 上的动点,连接 ,过点E作 的垂线交 于点N,垂足为H.以下结论:① ;② ;③ ;④连接 ,则 的最小值为 ;其中正确的结论是.(所有正确结论的序号都填上).
三、解答题
-
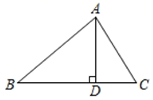
17. 计算:18. 先化简,再求值 ,其中x= .19. 如图,在 中, 于点D,若 . , ,求 的值.
 20. 随着智能手机的普及率越来越高以及移动支付的快捷高效性,中国移动支付在世界处于领先水平,为了解人们平时最喜欢用哪种移动支付方式,因此在某步行街对行人进行随机抽样调查,以下是根据调查结果分别整理的不完整的统计表和统计图.
20. 随着智能手机的普及率越来越高以及移动支付的快捷高效性,中国移动支付在世界处于领先水平,为了解人们平时最喜欢用哪种移动支付方式,因此在某步行街对行人进行随机抽样调查,以下是根据调查结果分别整理的不完整的统计表和统计图.移动支付方式
支付宝
微信
其他
人数/人
200
75

请你根据上述统计表和统计图提供的信息.完成下列问题:
(1)、在此次调查中,使用支付宝支付的人数为人,表示微信支付的扇形所对的圆心角度数为度.(2)、某天该步行街人流量为10万人,其中30%的人购物并选择移动支付,请你依据此次调查获得的信息估计一下当天使用微信支付的人数.(3)、甲、乙、丙三人都只习惯使用支付宝和微信支付,并且他们选择这两种支付的可能性是相同的,请计算三人恰好选择同一种支付方式的概率.21. 如图, 是 的直径,点A在 上, ,垂足为D, , 分别交 、 于点 F、G. (1)、证明: ;(2)、若 ,求弧EC的长度.22. 如图,某中学准备在校园里利用围墙的一段MN,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌40m长的墙的材料.
(1)、证明: ;(2)、若 ,求弧EC的长度.22. 如图,某中学准备在校园里利用围墙的一段MN,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌40m长的墙的材料. (1)、当AB长度是多少时,矩形花园的面积为150m2;(2)、能否围成矩形花园面积为210m2 , 为什么?23. 如图,在正方形 中,点 为对角线 , 交点, 平分 交 于点 ,交 于点 .
(1)、当AB长度是多少时,矩形花园的面积为150m2;(2)、能否围成矩形花园面积为210m2 , 为什么?23. 如图,在正方形 中,点 为对角线 , 交点, 平分 交 于点 ,交 于点 . (1)、求证: .(2)、判断 的形状.(3)、若 ,求 的长.24. 如图,抛物线 ( )与x轴交于 , ,与y轴交于点C.
(1)、求证: .(2)、判断 的形状.(3)、若 ,求 的长.24. 如图,抛物线 ( )与x轴交于 , ,与y轴交于点C.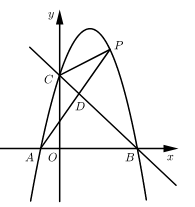 (1)、求点C的坐标和抛物线的解析式;(2)、点P是第一象限抛物线上的一个动点,连接 ,交直线 于点D.
(1)、求点C的坐标和抛物线的解析式;(2)、点P是第一象限抛物线上的一个动点,连接 ,交直线 于点D.①若 ,试求四边形 的面积S;
②设 的面积为 , 的面积为 ,求 的最大值.
25. 定义:二元一次不等式是指含有两个未知数(即二元),并且未知数的次数是1次(即一次)的不等式;满足二元一次不等式(组)的x和y的取值构成有序数对 ,所有这样的有序数对 构成的集合称为二元一次不等式(组)的解集,如: 是二元一次不等式, 是该不等式的解.有序实数对可以看成直角坐标平面内点的坐标,于是二元一次不等式(组)的解集就可以看成直角坐标系内的点构成的集合. (1)、已知 , , , 四个点.请在直角坐标系中标出这四个点,这四个点中是 的解的点是.(2)、设 的解集在坐标系内所对应的点形成的图形为G.
(1)、已知 , , , 四个点.请在直角坐标系中标出这四个点,这四个点中是 的解的点是.(2)、设 的解集在坐标系内所对应的点形成的图形为G.①求G的面积;
②反比例函数 ( )的图象和图形G有公共点,求k的取值范围;
(3)、设 的解集围成的图形为M,直接写出抛物线 与图形M有交点时m的取值范围.