湖北省孝感市孝南区2021年数学第二次学业水平监测试卷
试卷更新日期:2021-11-03 类型:中考模拟
一、单选题
-
1. 下列各数中比 小的数是( )A、0 B、 C、 D、2. 2020年12月8日,国家主席习近平同尼泊尔总统班达里互致信函,共同宣布珠穆朗玛峰最新高度8848.86米,其中8848.86用科学记数法表示为 ,则n为( )A、3 B、4 C、5 D、63. 下列计算正确的是( )A、2a+3a=6a B、a2+a3=a5 C、a8÷a2=a6 D、(a3)4=a74. 下列几何体中,主视图和左视图不一样的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图是济南市一周内日最高气温的折线统计图,关于这7天的日最高气温的说法正确的是( )
5. 如图是济南市一周内日最高气温的折线统计图,关于这7天的日最高气温的说法正确的是( ) A、最高气温是28℃ B、众数是28℃ C、中位数是24℃ D、平均数是26℃6. 如图,直线l1 l2 , 将含30°角的直角三角板按如图方式放置,直角顶点在l2上,若∠1=76°,则∠2=( )
A、最高气温是28℃ B、众数是28℃ C、中位数是24℃ D、平均数是26℃6. 如图,直线l1 l2 , 将含30°角的直角三角板按如图方式放置,直角顶点在l2上,若∠1=76°,则∠2=( ) A、36° B、45° C、44° D、64°7. 已知锐角∠AOB , 如图,(1)在射线OA上取一点C , 以点O为圆心,OC长为半径作 ,交射线OB于点D , 连接CD;(2)分别以点C , D为圆心,CD长为半径作弧,两弧交于点P , 连接CP , DP;(3)作射线OP交CD于点Q . 根据以上作图过程及所作图形,下列结论中错误的是( )
A、36° B、45° C、44° D、64°7. 已知锐角∠AOB , 如图,(1)在射线OA上取一点C , 以点O为圆心,OC长为半径作 ,交射线OB于点D , 连接CD;(2)分别以点C , D为圆心,CD长为半径作弧,两弧交于点P , 连接CP , DP;(3)作射线OP交CD于点Q . 根据以上作图过程及所作图形,下列结论中错误的是( ) A、CP∥OB B、CP=2QC C、∠AOP=∠BOP D、CD⊥OP8. 如图,Rt△ABC中,∠C=90°,AB=5cm,AC=4cm,点P从点A出发,以1cm/s的速度沿A→C向点C运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C向点C运动,直到它们都到达点C为止.若△APQ的面积为S(cm2),点P的运动时间为t(s),则S与t的函数图象是( )
A、CP∥OB B、CP=2QC C、∠AOP=∠BOP D、CD⊥OP8. 如图,Rt△ABC中,∠C=90°,AB=5cm,AC=4cm,点P从点A出发,以1cm/s的速度沿A→C向点C运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C向点C运动,直到它们都到达点C为止.若△APQ的面积为S(cm2),点P的运动时间为t(s),则S与t的函数图象是( ) A、
A、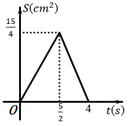 B、
B、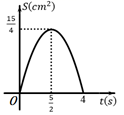 C、
C、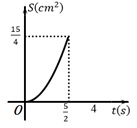 D、
D、
二、填空题
-
9. 若分式 无意义,则 =.10. 已知a,b是方程 的两根,则 的值是 .11. 不等式组 的解是.12. 如图,一架长为 米的梯子 斜靠在一竖直的墙 上,这时测得 ,如果梯子的底端 外移到 ,则梯子顶端 下移到 ,这时又测得 ,那么 的长度约为米.( , , , )
 13. 某校在“祖国好、家乡美”主题宣传周里推出五条A、B、C、D、E旅游线路.某校摄影社团随机抽取部分学生举行“最爱旅游路线”投票活动,参与者每人选出一条心中最爱的旅游路线,社团对投票进行了统计,并绘制出如下不完整的条形统计图和扇形统计图.全校2400名学生中,请你估计,选择“C”路线的人数约为.
13. 某校在“祖国好、家乡美”主题宣传周里推出五条A、B、C、D、E旅游线路.某校摄影社团随机抽取部分学生举行“最爱旅游路线”投票活动,参与者每人选出一条心中最爱的旅游路线,社团对投票进行了统计,并绘制出如下不完整的条形统计图和扇形统计图.全校2400名学生中,请你估计,选择“C”路线的人数约为. 14. 生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下 与全身 的高度比值接近0.618,可以增加视觉美感.若图中 为2米,则 约为.
14. 生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下 与全身 的高度比值接近0.618,可以增加视觉美感.若图中 为2米,则 约为. 15. 如图,曲线 和 是两个半圆, ,大半圆半径为2,则阴影部分的面积是.
15. 如图,曲线 和 是两个半圆, ,大半圆半径为2,则阴影部分的面积是. 16. 如图,在 中, , , 的平分线交CD于F,交AD的延长线于点E,作 ,垂足为G, .下列结论:① 为等腰三角形;② ;③ ;④ .其中正确的序号为.
16. 如图,在 中, , , 的平分线交CD于F,交AD的延长线于点E,作 ,垂足为G, .下列结论:① 为等腰三角形;② ;③ ;④ .其中正确的序号为.
三、解答题
-
17. 计算: .18. 3月初某商品价格上涨,每件价格上涨 20%.用 3000 元买到的该商品件数比涨价前少 20 件.3 月下旬该商品开始降价,经过两次降价后,该商品价格为每 件 19.2 元.
(1)、求 3 月初该商品上涨后的价格;
(2)、若该商品两次降价率相同,求该商品价格的平均降价率.
19. 某校有4个测温通道,分别记为A、B、C、D,学生可随机选取其中的一个通道测温进校园,某日早晨该校所有学生体温正常.(1)、小王同学该日早晨进校园时,选择A通道测温进校园的概率是;(2)、小王和小李两同学该日早晨进校园时,请用面树状图或列表法求选择不同通道测温进校园的概率.20. 如图,过点A(0,﹣2),B(4,0)的直线与反比例函数y= (x>0)的图象交于点C(6,a),点N在反比例函数y= (x>0)的图象上,且在点C的左侧,过点N作y轴的平行线交直线AB于点Q. (1)、求直线AB和反比例函数的表达式;(2)、若 ANQ面积为 ,求点N的坐标.21. 如图,点A、B、C、D均在 上,直径BC平分 , // 交BD于点M,延长BD至点N,使得 ,连接CN.
(1)、求直线AB和反比例函数的表达式;(2)、若 ANQ面积为 ,求点N的坐标.21. 如图,点A、B、C、D均在 上,直径BC平分 , // 交BD于点M,延长BD至点N,使得 ,连接CN. (1)、求证:CN与 相切;(2)、若 , ,求AB的长.22. 某商店经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
(1)、求证:CN与 相切;(2)、若 , ,求AB的长.22. 某商店经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200-2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)、求出y与x的函数关系式;(2)、问销售该商品第几天时,当天销售利润最大,最大利润是多少?


