广西贺州市八步区2021年数学初中学业水平模拟考试试卷(一)
试卷更新日期:2021-11-03 类型:中考模拟
一、单选题
-
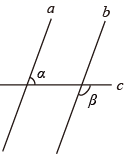
1. -2的相反数是( )A、2 B、-2 C、 D、2. 如图,直线 、 与直线 相交,且 ,若 ,则 的度数( )
 A、 B、 C、 D、3. 4的平方根是( )A、2 B、±2 C、 D、±4. 下列图形中既是中心对称图形又是轴对称图形的是( )A、
A、 B、 C、 D、3. 4的平方根是( )A、2 B、±2 C、 D、±4. 下列图形中既是中心对称图形又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 学校决定从甲、乙、丙三名学生中随机抽取两名介绍学习经验,则同时抽到乙、丙两名同学的概率为( )A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、(3a3)2=9a6 D、7. 下列几何体中,主视图是矩形的是( )A、
5. 学校决定从甲、乙、丙三名学生中随机抽取两名介绍学习经验,则同时抽到乙、丙两名同学的概率为( )A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、(3a3)2=9a6 D、7. 下列几何体中,主视图是矩形的是( )A、 B、
B、 C、
C、 D、
D、 8. 已知关于x的不等式组 仅有三个整数解,则a的取值范围是( )
8. 已知关于x的不等式组 仅有三个整数解,则a的取值范围是( )
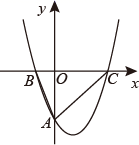
A、 ≤a<1 B、 ≤a≤1 C、 <a≤1 D、a<19. 如图,等腰 , , 点为 的中点, 将 的周长分成长为 和 的两部分,则等腰 的腰长为( ) A、 B、 C、 或 D、10. 函数 与抛物线 的图象可能是( ).A、
A、 B、 C、 或 D、10. 函数 与抛物线 的图象可能是( ).A、 B、
B、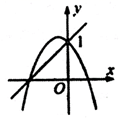 C、
C、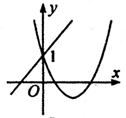 D、
D、 11. 如图所示,某盏路灯照射的空间可以看成如图所示的圆锥,它的高 米,底面半径 米,则圆锥的侧面积是多少平方米(结果保留 )( )
11. 如图所示,某盏路灯照射的空间可以看成如图所示的圆锥,它的高 米,底面半径 米,则圆锥的侧面积是多少平方米(结果保留 )( ) A、 B、 C、 D、12. 观察如下图形,它们是按一定规律排列的,依照次规律,第n的图形中共有210个小棋子,则n等于( )
A、 B、 C、 D、12. 观察如下图形,它们是按一定规律排列的,依照次规律,第n的图形中共有210个小棋子,则n等于( ) A、20 B、21 C、15 D、16
A、20 B、21 C、15 D、16二、填空题
-
13. 如果 与 是同类项,那么 .14. 分解因式:x3-x= .15. 一组数据-2,-1,0,1,2的方差是.16. 若 ,则 的值为.17. 如图,将半径为4cm的圆形纸片折叠后,圆弧恰好经过圆心O ,则折痕AB的长度为cm.
 18. 如图, 和 全等, , , 在同一直线上,连接 ,与 交于点 , , ,则 .
18. 如图, 和 全等, , , 在同一直线上,连接 ,与 交于点 , , ,则 .
三、解答题
-
19. 计算: .20. 解分式方程:21. 随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将检查结果绘制成下面两个统计图.

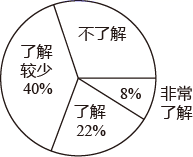 (1)、本次调查的学生共有 ▲ 人,并补全条形统计图;(2)、估计该校2400名学生中“不了解”的人数是人;(3)、“非常了解”的 人中有两名男生和两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.22. 如图,在平行四边形ABCD中, ,BE平分 交CD于O,交AD延长线于E,连接CE.
(1)、本次调查的学生共有 ▲ 人,并补全条形统计图;(2)、估计该校2400名学生中“不了解”的人数是人;(3)、“非常了解”的 人中有两名男生和两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.22. 如图,在平行四边形ABCD中, ,BE平分 交CD于O,交AD延长线于E,连接CE. (1)、求证:四边形BCED是菱形;(2)、若 , ,求 的面积.23. 如图,某中学数学课外学习小组想测量教学楼 的高度,组员小方在 处仰望教学楼顶端 处,测得 ,小方接着向教学楼方向前进到 处,测得 ,已知 , , .( ,)
(1)、求证:四边形BCED是菱形;(2)、若 , ,求 的面积.23. 如图,某中学数学课外学习小组想测量教学楼 的高度,组员小方在 处仰望教学楼顶端 处,测得 ,小方接着向教学楼方向前进到 处,测得 ,已知 , , .( ,) (1)、求 的值;(2)、求教学楼 的高度.(结果精确到 )24. 某水果批发商场经销一种高档水果,如果每千克盈利 元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.(1)、若每千克涨价3元,则每天可售出多少千克?(2)、现该商场要保证每天盈利6080元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
(1)、求 的值;(2)、求教学楼 的高度.(结果精确到 )24. 某水果批发商场经销一种高档水果,如果每千克盈利 元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.(1)、若每千克涨价3元,则每天可售出多少千克?(2)、现该商场要保证每天盈利6080元,同时又要使顾客得到实惠,那么每千克应涨价多少元?